本記事では非圧縮性のナビエストークス方程式がレイノルズ数によって流れのパターンが決まるということを示す力学的相似性について解説をします。
流体力学で大事な無次元量であるレイノルズ数について説明します。
レイノルズ数は、
\(Re=\frac{LV}{\nu}\)
↑こんな感じです。
↓ナビエストークス方程式について怪しい方は、こちらの記事をまずはお読みください。
力学的相似性
外力\(\boldsymbol{K}\)がないとした場合を考えた時、非圧縮性流体として取り扱える場合の運動方程式は以下のようになります。
数理計算しやすい形に変更:無次元化
(1)式をそのまま取り扱うのも良いかと思いますが、数値計算上もっとやりやすい形に変更できるならばその方が良いと考えられます。
この場合は、ある特徴的なスケールを用いて(1)を式変形した方が良いことが知られています。
- 代表的な長さL
- 代表的な速度V
すると、
代表的な時間は\(\frac{L}{V}\)、代表的な圧力は\(\rho V^2\)
上記のように考えると、無次元量は以下のようになります。
- 距離\({x}’=x/L\)
- 速度\({\boldsymbol{v}}’=\frac{\boldsymbol{v}}{\boldsymbol{V}}\)
- 時間\({t}’=\frac{t}{L/V}\)
- 圧力\({P}’=\frac{P}{\rho V^2}\)
となるので、(1)の式はとてもシンプルになります。
一応式変形を一つだけ示しておきます。
例えば、
\(\frac{\partial \boldsymbol{v}}{\partial t}\)なら、
上記のようなことを施すと(1)式は、
となります。
ここで、\(Re\)はレイノルズ数と言います。
レイノルズ数は\(Re=\frac{LV}{\nu}\)です。
(2)式にすると何が嬉しいかと言うと、(2)式の特徴的な量がレイノルズ数\(Re\)だけになってしまいました。ということは、流れのパターンはレイノルズ数\(Re\)だけを気にすればよいということになります。
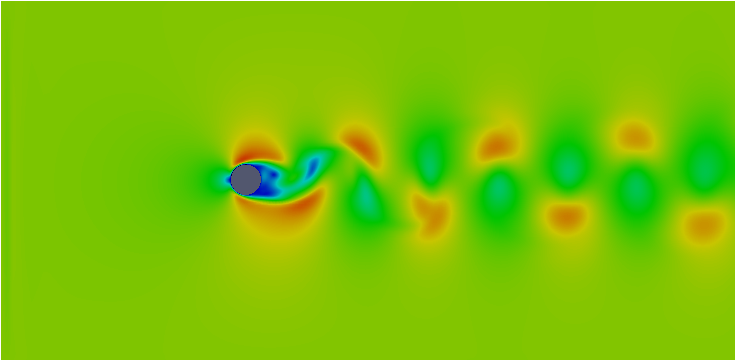
もし、下記のように「円柱回りの流体解析」をしたとすれば、レイノルズ数Reさえ揃っていれば解析上は同じ流れになるということですね。
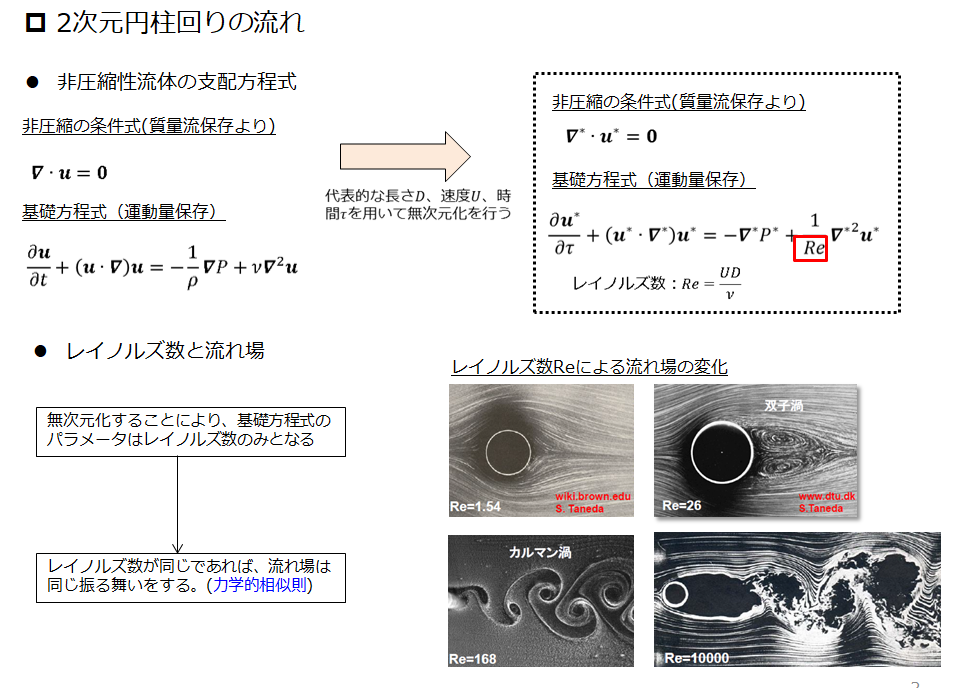
例えば・・・レイノルズ数\(Re=\frac{LV}{\nu}\)が同じ以下の場合を考えます。
- ケース1:円柱直径10m、速度2m/s
- ケース2:円柱直径5m、速度4m/s
いずれもレイノルズ数は同じ値になります。
ゆえに、流れのパターンも同じになるということですね。
これが流体力学の理論上で導ける力学的相似性です。
まとめ
※実用上は、例えば大きな形状周りの流れを実験でできないので、小さな形状にしてやりたくなるのですが、その場合は実際の流れを再現するのに流れを速くしなければなりません。いずれにしても形状を小さくすれば、流れを速くしなければならないなど実験で無理が生じることが多いです。
また、レイノルズ数だけをそろえたからと言って、実際は重力であったり外力もあったり、レイノルズ数だけ合わせても全く同じ流れにならないということになりますので、結局は実際の形状で数値計算をしなければならないということになります。
ただ、レイノルズ数を知ることである程度流れのパターンを知ることができるので、乱流の遷移やメッシュサイズ(渦サイズから判断)などの決定にはレイノルズ数は良い判断材料になると言えます。
次回
上記の円柱回りの2次元流体解析をオープンソースのOpenFOAMを用いてやってみましょう♪
そして、やったのがこちらです。