どうも(^^)/
僕は、流体のプロではありません(´・ω・`)
見習い程度のお勉強って感じで書いています。
(ハードルを下げておきます(笑))
以前に、↓下記の記事で流体における微小じょう乱は音速で伝播するというのを紹介しましたので、その続きです。
本記事
マッハ数を指標として微小じょう乱が伝播する様子を描いてみる
微小じょう乱とは
微小じょう乱が音速で伝播するというのは非常に重要な知識です。
微小じょう乱と言っているのは、例えば・・・
「ある時刻において、ある場所(観測点)における流速\(v\)であったとします。そこからちょっと時間が経って(\(\delta t\)とする)速度が\(v+\delta v\)になったとします。その微小に変化した情報が伝播するのが音速程度である(音速で周囲に伝わる)」ということを意味しています。
その微小じょう乱の情報がどう伝わるかどうかを理解することは流体現象を理解する上でとても重要になります。
その指標になるのがマッハ数です。
マッハ数
\(M=\frac{u}{a}\)
\(u\):流速
\(a\):音速
なので、マッハ数を横軸にとって流体の全体像を描いてみました。
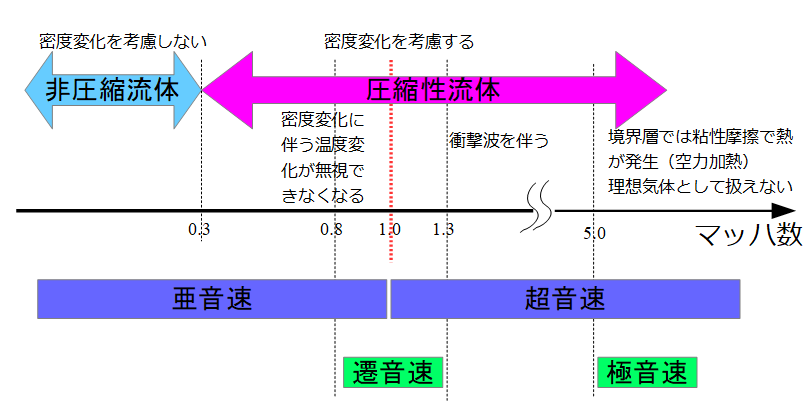
流体を勉強していると、「非圧縮性流体」「圧縮性流体」と区別して扱う場合がありますが、これは「~として扱う」という意味であって、突然流体の性質が変わるとかいう解釈をしてはいけません。
あくまで密度変化を「何%以内なら密度変化は無視して取り扱う」という数理モデルのお話なので、それがあたかも流体の性質そのものであると解釈してはいけないのでご注意ください。
こういった例は、他にもあります。
たとえば、理想気体もその例です。
ここでもやはり気体ならば理想気体であるとかいう理解をしてはいけません。
理想気体も、気体状態が希薄で「分子間力を無視する」「粒子の体積を考慮しない」という仮定のもとでの数理モデルに過ぎません。
↓こちらに少々その辺を触れています。
もし、「分子間力を無視する」「粒子の体積を考慮しない」という過程が成り立たないと考えられるならばファンデルワールスの状態方程式やビリアル展開などで実在気体に近い理論式を使う方が良いです。
では、なんでも厳密に考えれば良いのかというとそれはそれでナンセンスです。
ここの現象は分子レベルなのであるから、量子力学を用いるのでしょうか?
そもそもナビエストークス方程式自体も、大多数の分子の集まりとしてマクロな視点で立てた数理モデルなので、何もかも厳密に解くこと自体意味がないことです。
むしろ、シンプルな数理モデルでかなりの精度で現象を予測できる方が賢いやりかたであると思う(個人的に思う)ので、要するに使い分けかと思います。
「マッハ数に応じてこのような性質が突然現れる」という解釈ではなく、
あくまで、「マッハ数を指標にするとこのような性質があるので、それをどこまで考慮するか、考慮してどのように取り扱うか」という視点が重要であると考えています。
では、微小じょう乱が伝播する様子をマッハ数ごとに見ていきたいと思います。
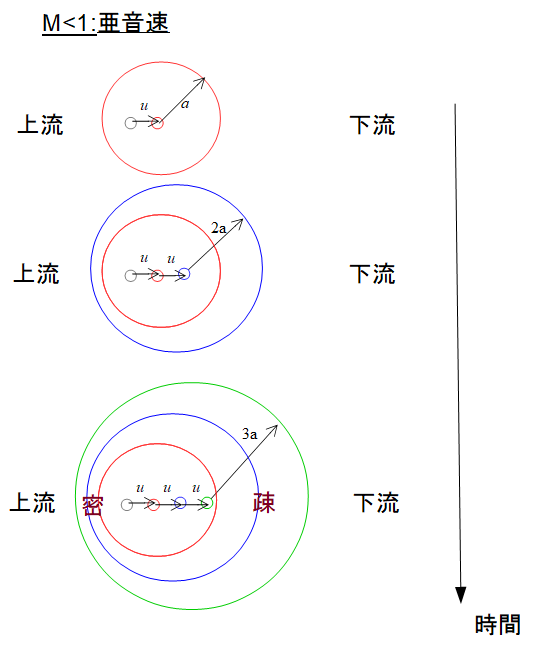
亜音速
流速が音速より遅い場合です。
時間ともに微小じょう乱が周囲に伝播しているのが描けているかと思います。
亜音速の場合は、微小じょう乱の情報は「上流側では密」「下流側では疎」になりながらも周囲全般に伝わっています。
粘性などの影響でこの微小じょう乱の減衰がなければ波面は無限遠まで伝わることになります。
非圧縮の流体として扱う場合は、マッハ数\(M=\frac{u}{a}→0\)なので、音速は無限大として扱っているので微小じょう乱は一瞬で周囲に伝わることになります。
だから、水などでは左側から押して圧力変化させると一瞬で右側に伝播します。
微小じょう乱の情報が届かない場合と言うのが次の例です。
音速
流速と音速が同じ場合(厳密に全く同じというのはありえませんが)は、絵でわかるように上流側に微小じょう乱の情報が伝わらないことがわかります。
ではもっと流速が速い(超音速)を考えましょう。
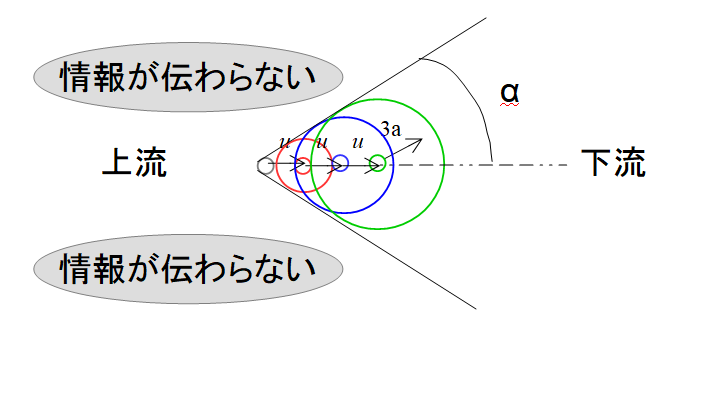
超音速
流速が音速より速い場合です。
こちらは絵を見てもらえればわかりますが、上流側に微小じょう乱の情報が伝わっていないのがわかるかと思います。
そりゃー情報を伝えようとしている音速より速い速度で走っているから後ろの方には何も情報が伝わりませんね(*_*;
ということで、微小じょう乱の情報が伝わる領域というのが絵で書いた角度\(\alpha\)の領域に限られているということになります。
幾何学的に、
という関係があることがわかります。
\(\alpha\)をマッハ角といいます。
※マッハ角は\(M<1\)では定義できません。
流体解析のお話
少し、流体解析の話も触れておきましょう。
流体解析をするにあたって、「扱おうとしている流体現象が、非圧縮性として取り扱っても良いか圧縮性を考慮して取り扱うべきか」で扱う方程式が変わってきて、それによって計算の複雑さや計算時間がずいぶんと変わってきます。
圧縮性を考量するかうかというのは、密度変化を考慮するかどうかということになるのですが、密度変動を考慮するどうかによって扱う方程式は変わります(↓下記記事参照)。
しかし、だからといって密度変化を考慮する(圧縮性を考慮する)かどうかで境界条件は変わるのでしょうか?
変わると言えば変わるのかもしれませんが、境界条件の本質的な区別というのはむしろ流速が音速と比較してどうかということの方が重要です。
↓こちらの記事で書いたように、亜音速領域であれば下流側の情報は上流側にも伝わるので非圧縮性の流体として扱ったか圧縮性の流体として扱ったかによって境界条件が変わることはないというのが理解できるかと思います。
しかし、超音速領域は境界条件が変わってきます。
↑この記事のまとめで何を書いたのかと言いますと、
取り扱う問題やもっている情報にもよりますが、境界条件として一般的なものとして、
亜音速
流入条件として、\(u,v,w,P,T\)のうち4つ、流出条件として1つの変数
だいたい、速度の3変数を流入条件にして、流入条件を圧力にする場合が多いでしょうかね。
その他の亜音速の場合の設定方法
(1)質量流量と\(T\)を与える方法
質量流量の変わりに\((u,v,w)\)を規定することも可能ですが、質量流量の方が収束性等の点で好ましい結果が得られることが多いです。
(2)全温度, 全圧を指定する方法。
境界での\(P\)や流量が未知である場合に用いることができます。例:流入口が大気開放である場合などによく用いられるます。
(3)\(P, T\)を規定する方法
流入してくる流体の\(P,T\)が既知で流速が未知という場合に適しています。
流出条件として、基本的に質量流量規定, 圧力規定の2つが考えられます。
流出口で逆流防止のため、圧力規定の代わりに全圧規定とする場合もあります。
※乱流解析の場合は、さらに変数として乱流エネルギー\(k\), 乱流消失率\(\epsilon\)を考慮する必要がありますが、これらの変数は流入口でその値を与えなければなりません。
↑圧縮性, 非圧縮性で扱いの違いはありません。
と、このように記事に書きました。
本記事を読めば、亜音速流れでは非圧縮性・圧縮性に関わらず下流側の圧力の情報はちゃんと上流側にも届くので上述の境界条件で問題ないと言えます。
さらに超音速に対しては、↑上の記事では「まとめ」で、
超音速
流入条件として、\(u,v,w,P,T\)、流出条件としてはひとつもいらない。
と書きましたが、本記事を読めば超音速流れでは上流側に微小じょう乱に情報が伝わらないことがわかります。
ですので、超音速流れで境界条件を考えるときは上記の設定をしなければならないことがうなずけると思います。
もし、超音速流れの場合に亜音速と同じ境界条件の設定をした場合(流出条件に圧力を設定)すると、上流側に圧力変動の情報が遡って伝わらないので問題が解けないことになります。
まとめ
マッハ数を指標として微小じょう乱が伝播する様子を描いてみました(^^)/