こんにちは(@t_kun_kamakiri)。
2つの量\(x\)と\(y\)の関係性を調べるのに、グラフにデータをプロットしていきその関係性を視覚的に見たりしますよね?
1次関数で近似したり、2次関数で近似したり・・・・色々近似曲線を当てはめて関係性を見るかもしれません。
「指数関数ならいい感じで近似曲線が描けそうなのにな~」
と思ったことがありませんか?
指数関数で近似できる場合:
例えばこんな感じ↓
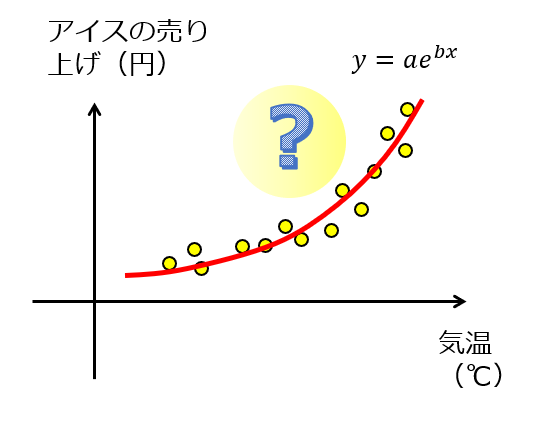
「1次関数で近似できる」場合と、「指数関数で近似できる」場合の考えを理解する。
「1次関数で近似する」場合と「指数関数で近似する」場合
イメージしやすいように、「気温とアイスの売り上げ」を例にとって話を進めていきます。
両者の関係性をイメージすると、気温が高いとアイスの売り上げが上がるというのがイメージできますよね。(価格は変動しないとします)
y=ax+b
\end{align*}
と書いて、両者の関係は「1次関数かな」って具合に表しますよね。
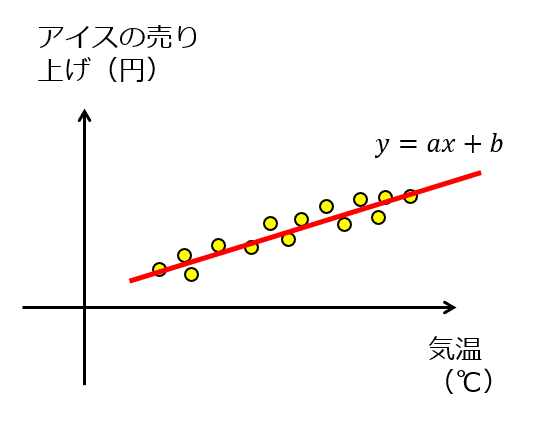

では、両者の関係式がどうやら「指数関数」で書けるのではないか?となった場合にどんなことをイメージするでしょう。



両者の関係性がずっと変わらないとき➡1次関数
両者の関係性がずっと変わらないという意味は、傾きが変わらないという意味です。
つまり、
だということを意味しています。


実際にそうですよね。
と近似式で関係性を表した場合に、傾きが変わらないかどうか微分して見てみましょう。
(2)式を微分すると、
となりますのでやはり傾きが変わらないということがわかります。
(3)式から言えることは、「気温が10℃から20℃に変わったときの売り上げの変化量も、気温が50℃から60℃に変わったときの売り上げの変化量変わらない」ということになります。
温度に対して、売り上げの増加の感度はどんな温度域を考えても同じだってことを言っているのです。
では指数関数の場合はどうでしょうか?
片方の変化に対して敏感(鈍感)に変わる➡指数関数
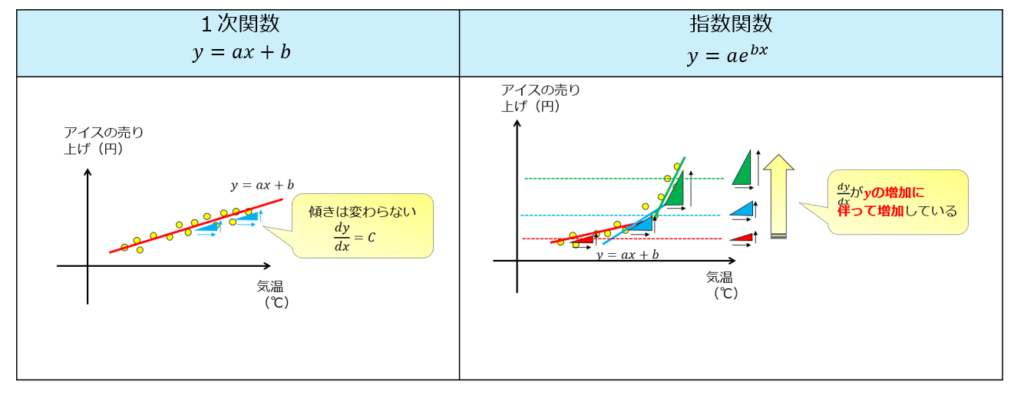
指数関数の関係性をわかりやすく3つの領域に分割(下図の右)してみましょう。
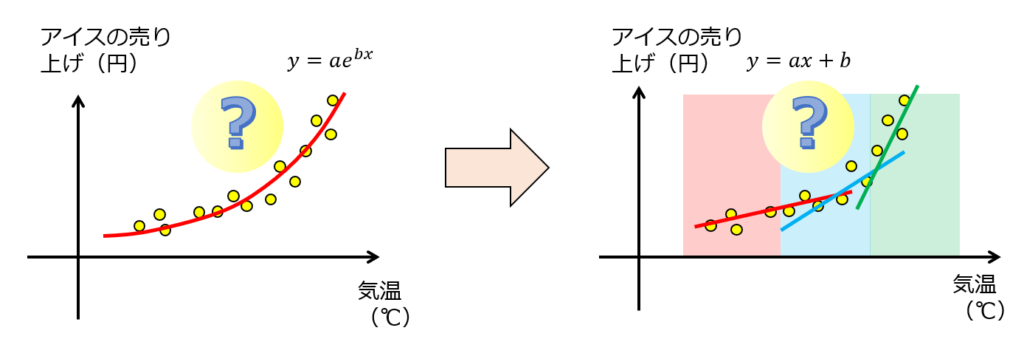

そうすると傾きが徐々に上昇しているのがわかるかと思います。
ほんとうにそうなのかどうかは、1次関数の時と同様に指数関数を微分してみれば良いです。
これを微分します。
※最後の式には(4)式を用いた。
(5)式を、下のように絵にしてみましょう。
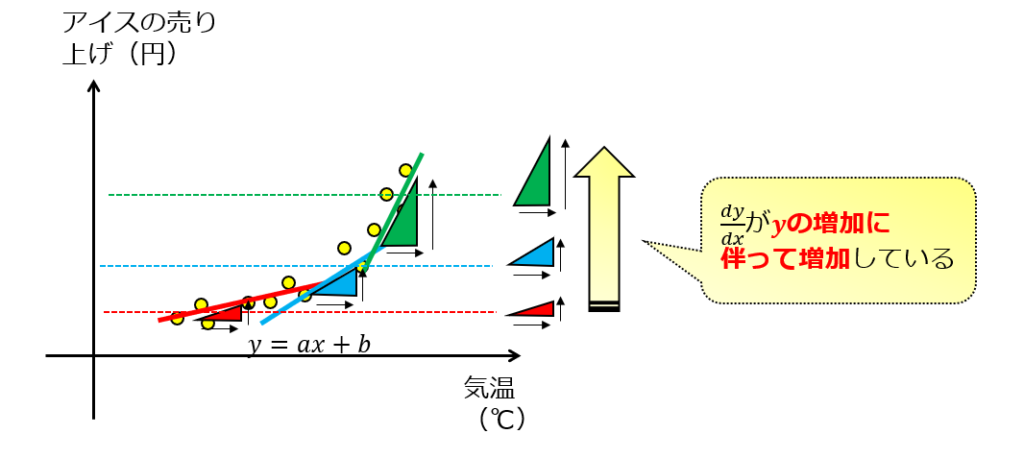

上図から、両者の関係性が指数関数である場合には、アイスの売り上げが高い領域では、変化率が大きくなっているということがわかります。
これは言い換えると、気温が高い領域ではアイスの売り上げが敏感に変わっているということなのです。
指数関数に従う場合の物理現象
両者の関係式を試験などを行い紙にプロットすれば、関係性は見えてくるかと思いますが、「あれ?これって指数関数で書ける関係式にあるんじゃないか?」って試験をせず関係性を予測することはできないのでしょうか?
実は物理の問題で指数関数的な関係性をもったものというのはよく登場します。
放射壊変をする原子核または素粒子が微小時間に壊変する確率を記述する関係式に、
というのがあります。
これも(5)式と同じ形をしていますよね。
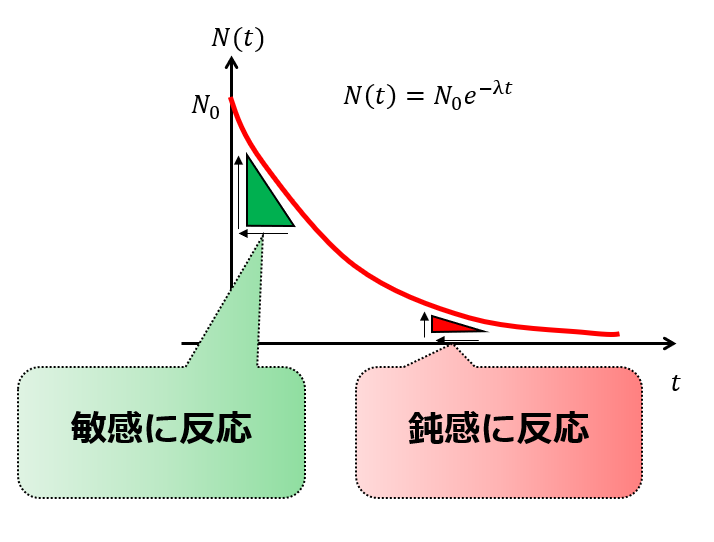
原子核だとか素粒子だとか話すと難しい話になるので、(6)式は「粒子数\(N\)が大きいと、単位時間あたりの粒子の減少量が大きい(あるいは、粒子数が小さいと単位時間あたりにあまり粒子は減らない)」と簡単に考えます。
言い換えると、粒子数\(N\)が多いと粒子数の減り方がめちゃくちゃ敏感に反応してどんどん減るよってことです。
文言だけみると、指数関数っぽいですよね。実際そうなのですが、確かめてみましょう。
(6)式を、
\frac{1}{N}\frac{dN}{dt}=-\lambda\tag{7}
\end{align*}
これを両辺\(t\)で積分します。
\log_{e}N=-\lambda t+C
\end{align*}
⇔
N(t)=N_{0}e^{-\lambda t}\tag{8}
\end{align*}
※\(N_{0}=e^{C}\)
となってやっぱり指数関数となりました。

関数の幅(スケール)を考えると物理的意味がわかる
(8)式から物理的意味をもう少し考えてみましょう。
出てきた関数のスケールを考えるというのは物理的な考察でよくすることです。
今回の場合は、指数関数の分母に\(\tau=\frac{1}{\lambda}\)を導入すると、関数の幅(スケール)というのを定義できます。


この\(\tau\)が大きいと、曲線の幅は大きくなり「なかなか時間が経っても粒子が減らないな~」ってなるわけです(下図)。
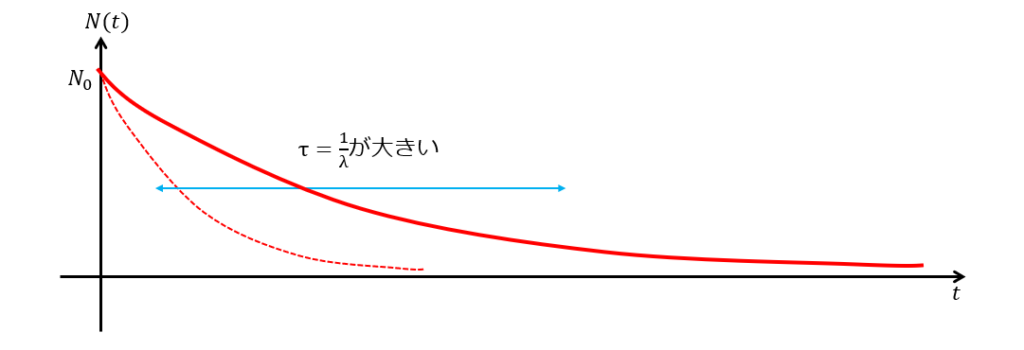

逆に、\(\tau\)が小さいと曲線の幅が狭くなり「あっという間に粒子が無くなってしまった」となるわけです(下図)。
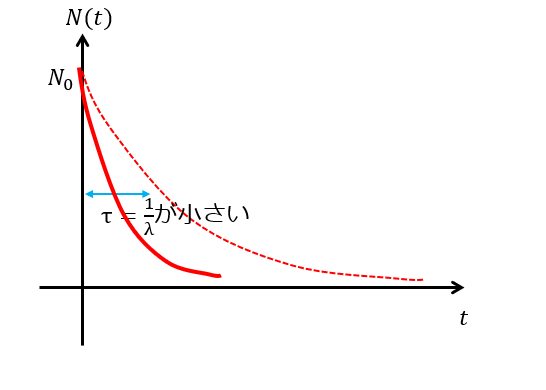

つまり、\(\tau\)は粒子の寿命は表す量になります。
まとめ
両者の関係式が「1次関数で近似できる」場合と、「指数関数で近似できる」場合の違いをまとめれたと思います。

指数関数で近似できるなら、片対数グラフを使うことをお勧めします(下記の記事が参考になります)。