こんにちは(@t_kun_kamakiri)。
小学生の理科の実験で、「片方を対数にしたグラフ:片対数グラフ」や「両方の軸を対数にしたグラフ:両対数グラフ」を扱ったことがある人もいるかもしれません。
- 「片対数グラフ(あるいは両対数グラフ)って何?
- なぜ片対数グラフ(あるいは両対数グラフ)を使うと直線になるのか?
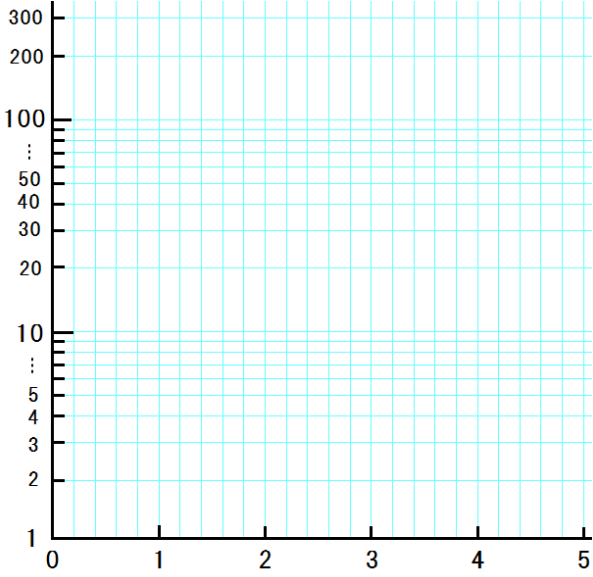
↑これが片対数グラフです。
昔、先生に「このよくわからない紙に計測した点をプロットしたら直線になるから黙って点でも打っていろ」なんて言われた方もいることでしょう。
このグラフに点を打てばなぜか直線になるのを不思議に思った人もいるかもしれません。
本記事では、なぜ直線になるのか理由を説明したいと思います。
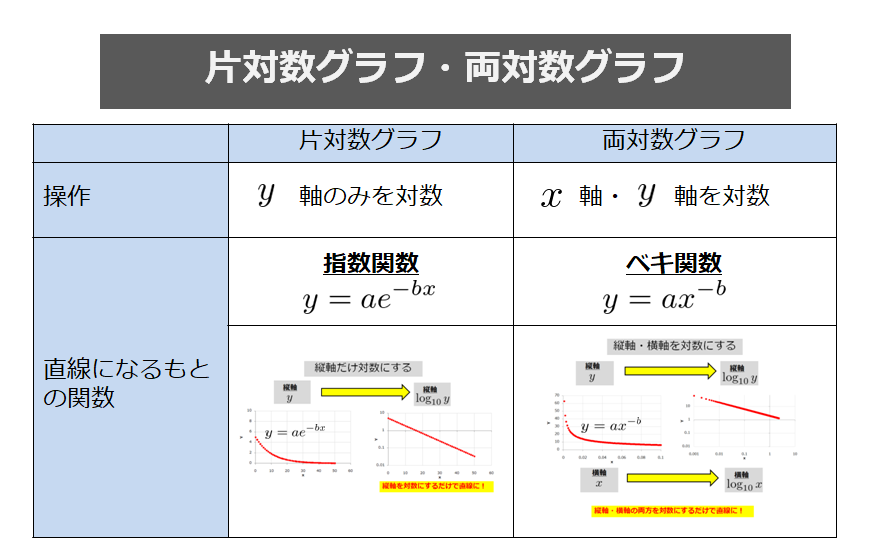
- 「片方を対数にしたグラフ:片対数グラフ」
- 「両方の軸を対数にしたグラフ:両対数グラフ」
「なぜこれらのグラフを使うと直線になるのか」、また「\(x\)と\(y\)にどういった関係性がある場合に片対数グラフを使うのか」を理解していきたいと思います。
片対数グラフだけではなく両対数グラフとの比較も書いておきます。
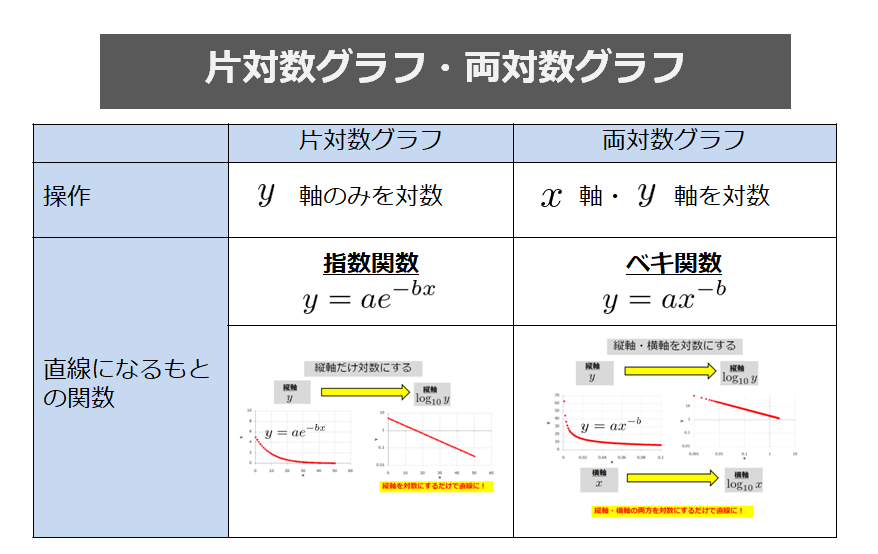
片対数グラフ
まず片対数グラフを使って直線になったものを見てみましょう。
片対数表示(y軸だけ対数)
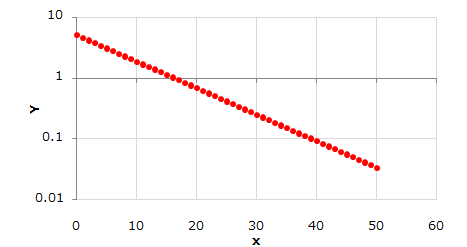
見てお分かりの通り、y軸は対数表示になっていますし、どう見ても直線になっていますよね。
不思議だな~って思うのですが全然不思議でもなんでもありません。
縦軸が対数表示ではなく、もともとの表示ならどうなっているのかを見るとどうなっているのかがわかります。
下図がもとのグラフ(対数を使わないグラフ)です。
元のグラフ(対数表示なし)
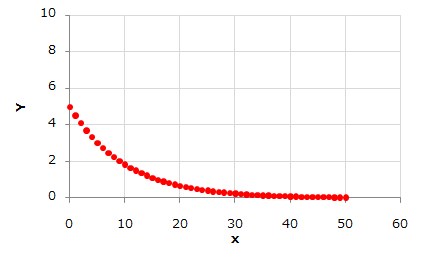
こんな感じです。全然直線ではありませんよね。
一体何が起こっているのでしょうか?
片対数グラフ:縦軸を対数にするだけで直線になる
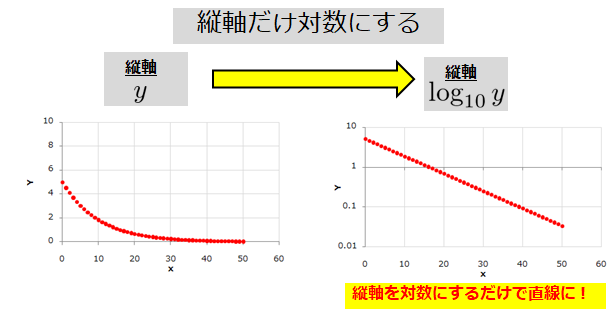
「縦軸を対数にするだけで直線になるような関係性が\(x\)と\(y\)にあった」というのがポイントになるわけです。
そのような関係性にあるものは何かというと指数関数です。
例えば、下記のような関係式が成立しているような場合などが当てはまります。
y=ae^{-bx}\tag{1}
\end{align*}
これが上図の左の関係式です。
つまり(1)式のような関係式(あるいはそれに近い関係式)がもともとあるから縦軸を対数にすれば直線になるということが「片対数グラフを使うとなぜか直線になる」ということのカラクリになります。
ならば、(1)式から「縦軸を対数にすれば本当に直線になるのか?」を確認してみれば良いでしょう。
片対数グラフ:(1)式を片対数表示変換
(1)式の両辺に\(log_{10}\)を作用させてみましょう。
となりますよね。
これをもう少し分解してまとめると、
⇔
ここで、
- \(\log_{10}y=Y\)
- \(b\log_{10}e=A\)
- \(\log_{10}a=B\)
とおくと、(3)式は
となり、「おー!!1次関数ではないか!直線の式ではないか」と感動するのです。
ここで何をしたかと言いますと、
- 両辺に対数(\(\log_{10}\)を作用させる
- \(y\)軸だけを対数表示にする:\(\log_{10}y=Y\)
この2点を行っただけです。
これが片対数グラフにすると直線になるカラクリです。
つまり、「もともとの\(x\)と\(y\)の関係性が指数関数を使った(\(y=ae^{-bx}\))の関係性があるから片対数グラフにすると直線になる」のです。
両対数グラフ
次は両対数グラフについて説明したいと思います。
今度は両方の軸が対数になっています。そしてお分かりの通り直線になっています。
両対数グラフ(x軸、y軸ともに対数表示)
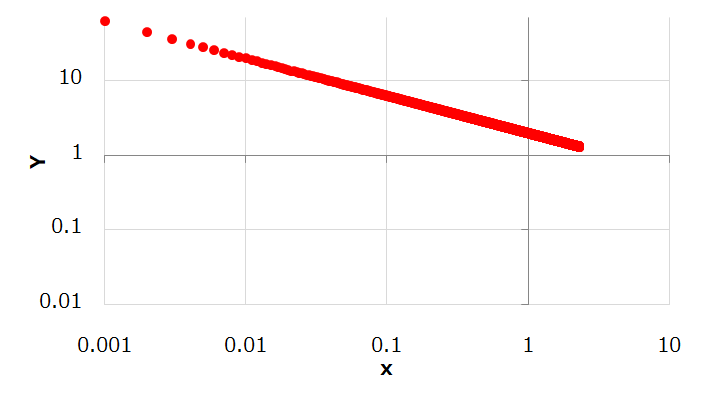
では、上図のグラフはもともとどんなグラフであったか見てみましょう。
それが↓こちらです。
元のグラフ(対数表示なし)
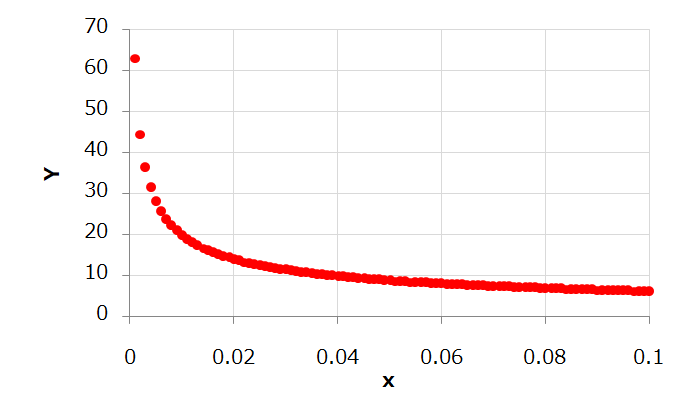
「なんだこれは?」となりますよね。
このグラフは一体どんな関係式を表しているのでしょうか。
両対数グラフ:縦軸・横軸を対数にするだけで直線になる
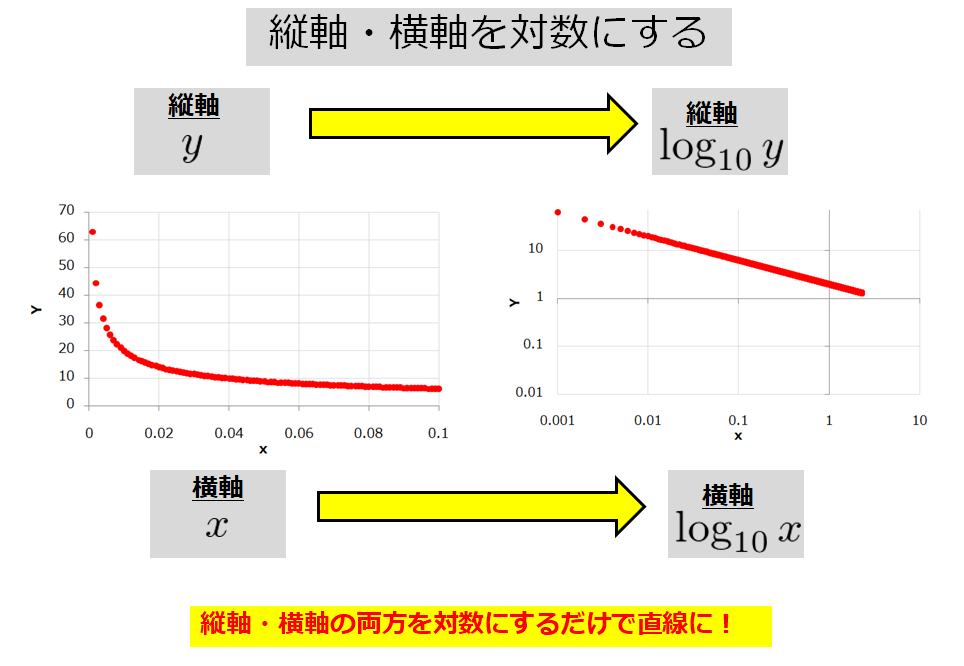
「縦軸・横軸の両方を対数にするだけで直線になるような関係性が\(x\)と\(y\)にあった」というのがポイントになるわけです。
そのような関係性にあるものは何かというとべき関数です。
例えば、下記のような関係式が成立しているような場合などが当てはまります。
これが上図の左の関係式です。
つまり(5)式のような関係式(あるいはそれに近い関係式)がもともとあるから縦軸・横軸を対数にすれば直線になるということが「両対数グラフを使うとなぜか直線になる」ということのカラクリになります。
ならば、片対数グラフでの解説で行ったように、(5)式から「縦軸・横軸を対数にすれば本当に直線になるのか?」を確認してみれば良いでしょう。
両対数グラフ:(5)式を両対数表示変換
(5)式の両辺に\(log_{10}\)を作用させてみましょう。
となりますよね。
これをもう少し分解してまとめると、
⇔
ここで、
- \(\log_{10}y=Y\)
- \(\log_{10}x=X\)
- \(\log_{10}a=B\)
とおくと、(7)式は
となり、「おー!!1次関数ではないか!直線の式ではないか」と感動するのです。
ここで何をしたかと言いますと、
- 両辺に対数(\(\log_{10}\)を作用させる
- \(y\)軸、\(x\)軸の両方を対数表示にする:\(\log_{10}y=Y\)、\(\log_{10}x=X\)
この2点を行っただけです。
これが両対数グラフにすると直線になるカラクリです。
つまり、「もともとの\(x\)と\(y\)の関係性がべき関数を使った(\(y=ax^{-b}\))の関係性があるから両対数グラフにすると直線になる」のです。
まとめ
では、もう少し踏み込んで・・・
どんな時に指数関数が成り立つような\(x\)と\(y\)の関係式になるのでしょうか?
おすすめの参考書
最後におすすめの参考書を紹介しておきましょう。

























[…] https://takun-physics.net/?p=4615 不自然なグラフだと思っちゃう人は、良い機会だからちょっと勉強して見てもいいかもね。 […]
[…] https://takun-physics.net/?p=4615 不自然なグラフだと思っちゃう人は、良い機会だからちょっと勉強して見てもいいかもね。 […]