前回の記事で、流体力学の運動量保存則である、
運動量保存則
\(\sigma_{ij}\)(コーシー応力)が何かということを説明しました。
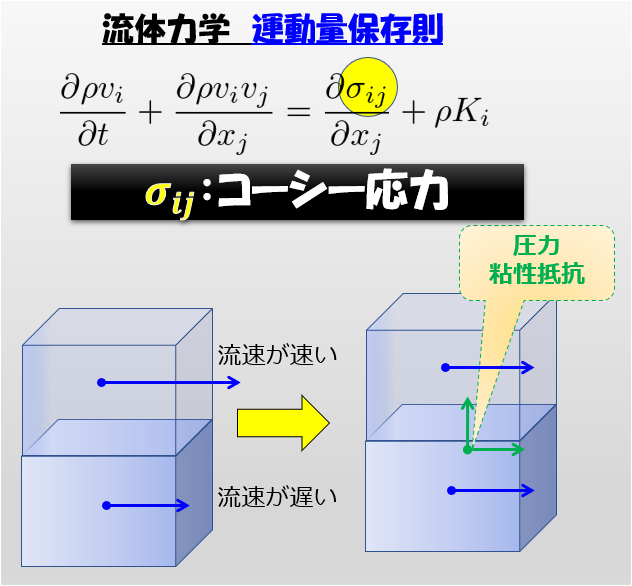
ただ上の記事で、コーシー応力は圧力と粘性抵抗であるという説明の記事を書きましたが、具体的な式を書いていませんでしたよね。
そこで・・・
コーシー応力の具体な式を示したいと思います。
\sigma_{11} & \sigma_{12} & \sigma_{13}\\
\sigma_{21} & \sigma_{22} & \sigma_{23}\\
\sigma_{31} & \sigma_{32} & \sigma_{33}
\end{pmatrix}\cdot\cdot\cdot (2)\end{align*}
↑結果はこれです。
連続体近似をした時の内力をどのように式で表現するかということですので、コーシー応力は、別に流体力学だけに出てくる応力ではなくて、材料力学などでもよく出てきます。
\(x\)軸に垂直な面の内部にかかる力を考える
内部にはたらく力を考えるわけですが、下記のように流れの領域のある1部分を切り取って2分割することを考えます。
まずは簡単のため、\(x\)軸に垂直な面で領域を2分割にしてみます。
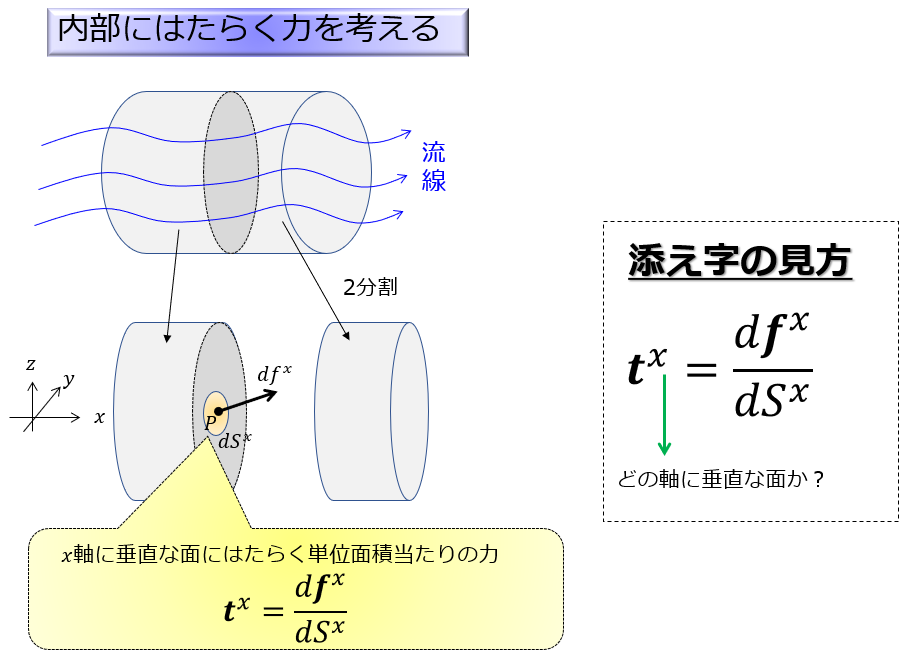
そして、分割した片方(左側)の面にはいわゆる内力というのがはたらいています。
この内力は右側の面から受けている力から来ています。
では、その面の上の点\(P\)での\(x\)軸に垂直な単位面積あたりの力を考えましょう。
とこうなりますよね。
- \(x\)方向の面:\(dS^{x}\)
- \(x\)方向にはたらく力:\(df^{x}\)
※注意ですが、別に\(x\)軸方向の力を考えたわけではなくて、\(x\)軸に垂直な面に対する単位面積あたりの力を考えたわけです。
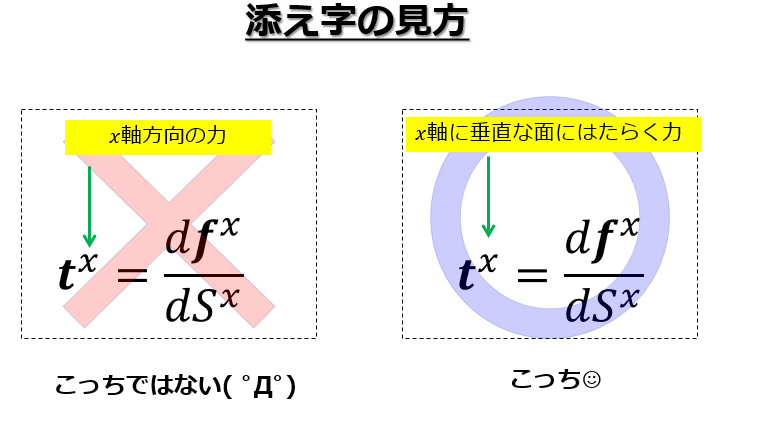
だから、\(x\)軸に垂直な面に対する力\(\boldsymbol{t}^{x}\)は、必ずしも面に対して垂直な方向の力とは限りません。
\(\boldsymbol{t}^{x}\)を\(x\)、\(y\)、\(z\)に分解する
左側だけの面位着目して\(x\)軸に垂直な面に対する力\(\boldsymbol{t}^{x}\)を\(x\)、\(y\)、\(z\)に分解することを考えます。
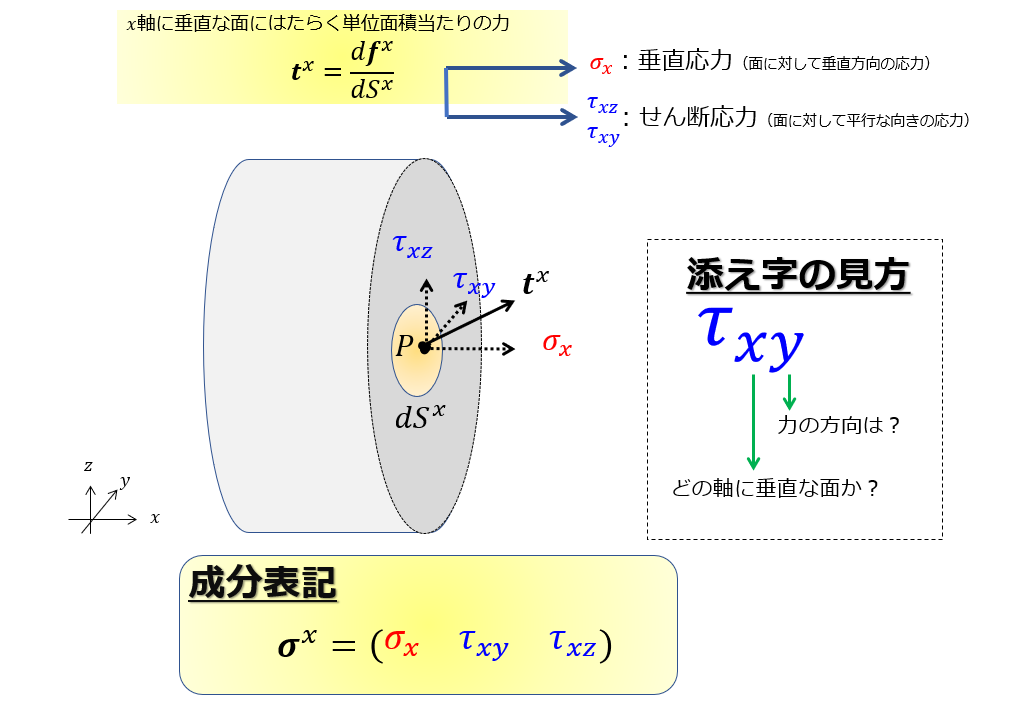
\(x\)、\(y\)、\(z\)軸に垂直な面の内部にかかる力を考える
先ほどまでは\(x\)軸に垂直な面にはたらく力しか書いていませんでしたが、\(x\)軸以外の軸についても同様の考え方ができるわけですよね。
わかりやすくするために点\(P\)のまわりを拡大して立方体を用意して見ましょう。
では、この立方体の表面に先ほど同様に応力を書いてみます。
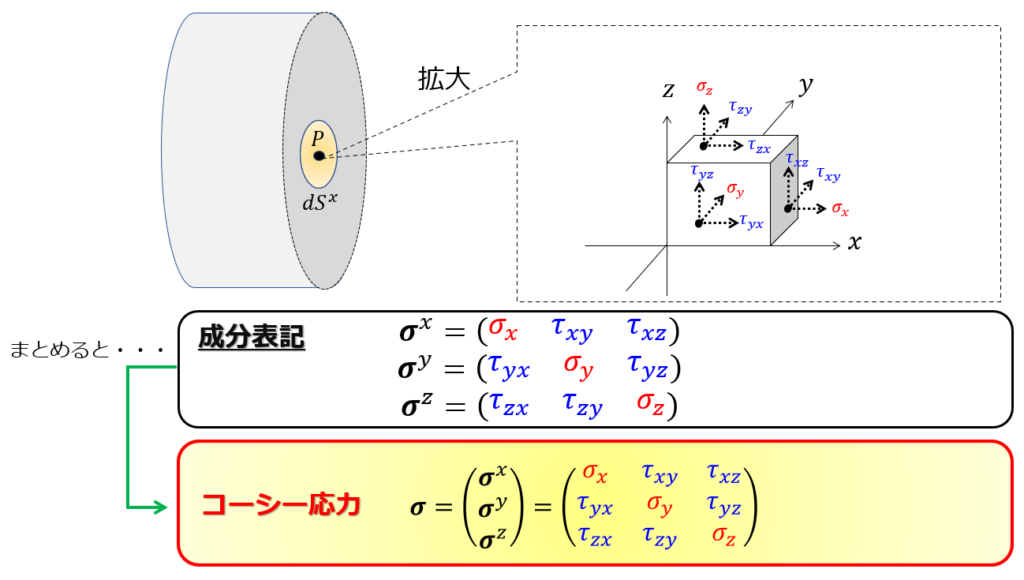
はい、こんな感じです。
こらがコーシー応力の式です。
添え字が文字だと後で添え字が足らなくなる可能性があるので、よく添え字は数字に置き換えることが多いです。
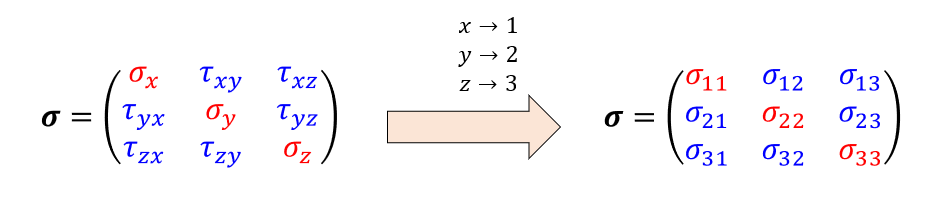
内部にはたらく力は、こんな感じでテンソル表記になります。
テンソル表記は苦手な人が多いかもしれませんが、順をおって理解していけばだんだん慣れてくると思います。
まとめ
添え字が2文字になると少々煩雑に見えますが、ポイントは
- どの面に垂直な力を考えているか
- どの軸の方向の力を考えているか
これを添え字で表現しているだけだと覚えていればOKです。
しかし、立方体だけだと限定され過ぎていないか?
本記事で書いた内部にはたらく力は、立方体で考えましたよね。
これって限定しすぎていないか?って思われる方もいるでしょう。
点Pを通る面なんて、無数に存在します。
だから任意の面に対する応力ベクトルとコーシー応力との関係を示しておく必要があります。別の記事で書くとして、結果だけ載せておきます。

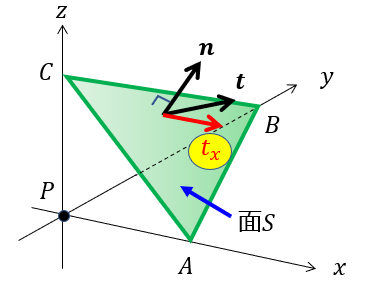



















点Pの周りを拡大したときの応力のところなのですが, z軸に対して垂直な面でz軸に働く垂直応力はσ_yではなくσ_zだと思います。
ご指摘ありがとうございます。
おっしゃる通りですね。修正いたしました。
ありがとうございます。