こんにちは(@t_kun_kamakiri)。
本日は、指数関数のお話をしたいと思います(^^)/
新型コロナウイルス感染者数が指数関数増加をしているというのが最近話題だからです。
↓現状どうなっているのでしょうか・・・・・
2020年4月現在、新型コロナウィルスの感染者が爆発的に増えてきていますね。
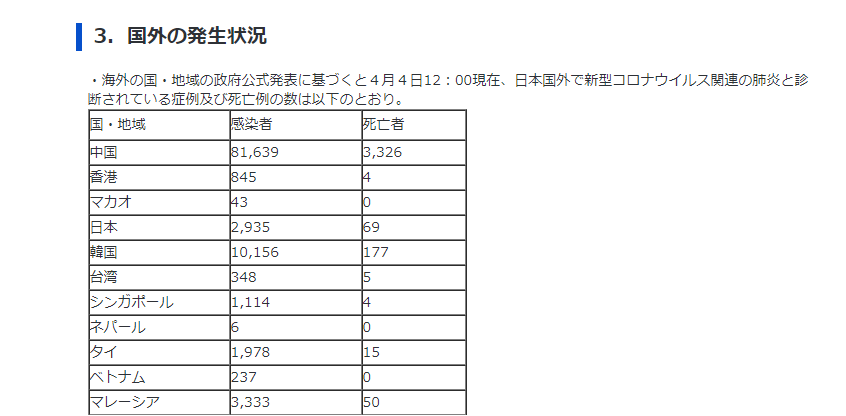
4/4では、日本での感染者数は約3000人となっています。
厚生労働省のホームページより
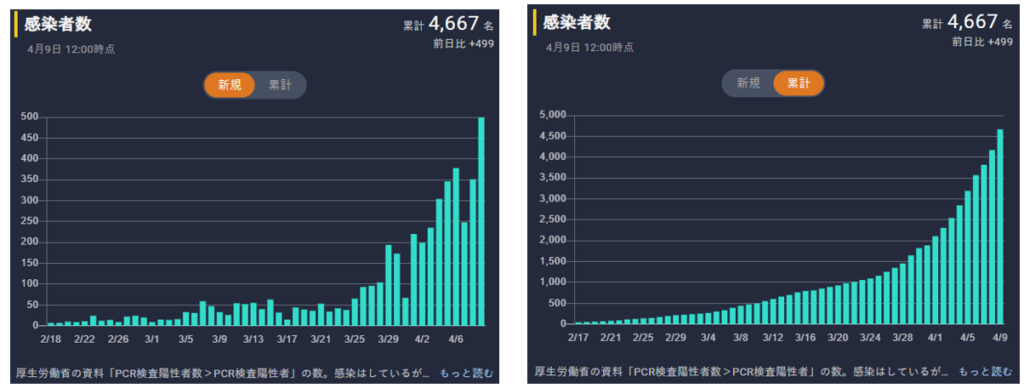
もうちょっとわかりやすくグラフにしてくれているサイトがあります。
東洋経済より
あれ?
4月6日は感染者数が約4700人になっています・・・・2日で1500人以上増えているという事でしょうか?
恐ろしい増え方です。
これが指数関数的増加ってやつですか・・・
この感染者の増加率を見て、次のように言う人もいるでしょう。
👆このようなことを言っていてはよくありません。
今自分にできることは何かを考えて、小さな事でもできることを実践していくことが大事だと考えております( `ー´)ノ
では、たまたまこの記事を読んでいる人はいったい何をしなくてはいけないのでしょうか?
政府を叩くことでもなく、電車通勤をやめることでもなく、外出禁止で引きこもる事でもありません。
今、この記事を読んでいる人が、
たった今・・・・
本当にやらなくてはいけないことは・・・・
指数関数について勉強することです!
( ^ω^)・・・
そうですよね。
だって、この記事は指数関数について書いているんですから(‘ω’)
では、前置きが長くなりましたが本記事の内容については以下となります。
- どのような時に指数関数増加になるのか?
- 指数関数は爆発的な増加なのか?
- 指数関数を片対数グラフで表現すると?
このような3つの内容で指数関数の特徴をお伝えします。
指数関数について語ると色々と長くなるのですが、厳選して3つに絞りました。
- 高校数学をまじめに勉強した方(それを有す者)
- 指数関数で政府を論破する人
※この記事はコロナ感染に関する学術的な議論をしているわけではありません。
あくまで「指数関数」についての記事を書いているだけです。
政府を叩くつもりも、医療関係者や患者さんへの批判などはいっさい含まれていません。
指数関数についての記事を書きたいだけです(;^ω^)
どのような時に指数関数増加になるのか?
1日当たりの感染者数について毎日のように報道されています。
そこで感じているのは、毎日急激に新規の感染者数が増えていっているという事です。
「毎日新規の感染者数が増えていること」と「総感染者数が指数関数的に増えている」というのは大きく関係しています。
ウイルスに感染の単純数理モデル
指数関数について理解をしやすくするために、今回のウイルス感染を例にとってとても単純なモデルで考えてみます。
【スタートは以下のように決める】
ある人がウイルスに感染してしまったとします。

ある日の総感染者数が4人であったとします。
※何かしらの経路で感染してしまったとしています。
ここで数理モデルのルールを定めます。
【ルール】
その感染者が一日に必ず別の誰かひとり感染するという場合を考えます。


めちゃくちゃ単純なモデルですよね( `ー´)ノ
こういった単純なモデルで総感染者数はどのような推移をたどるのでしょうか?という問題です。
1日目には新規の感染者と自分達も含めると「総数8人、新規4人」となります。
では、このルールに従って数日間を見てみましょう。
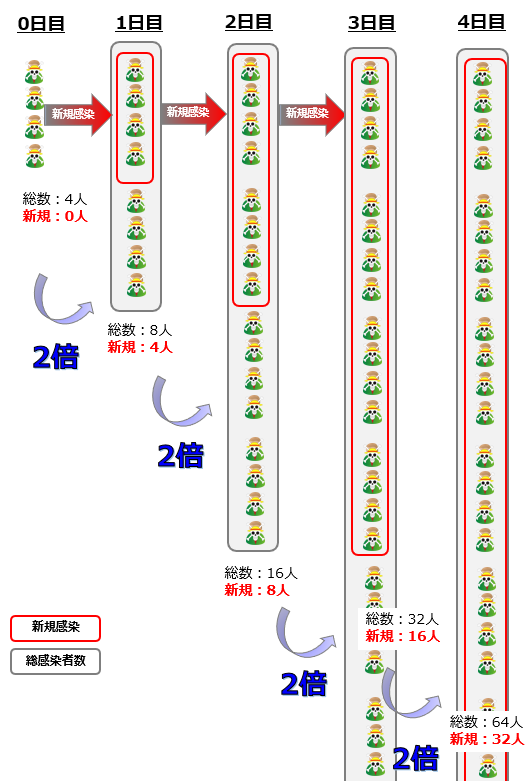

なんと4日後には「総数64人、新規32人」となってしまいました。
どうなっているのか一般化して考えてみます。
総感染者数が\(N\)、時間を\(t\)とします。
※時間については1秒としても、1日としてもそれは単位の話なのでここでは特にこだわりはありません。
が、わかりやすく時間軸の単位は「日」としておきましょうかね。
N(0) &=4\\
N(1) &=8=4\times 2\\
N(2) &=16=4\times 2\times 2\\
N(3) &=32=4\times 2\times 2\times2\\
\cdots\cdots\\
N(10) &=4096=4\underset{10回掛け算}{\underline{\times 2\times 2\times2\cdots}}\\
\cdots\cdots\\
N(t) &=4\times 2^t = 2^{t+2}\tag{1}
\end{align*}
こんな感じの増え方をするのです。
もちろん、感染した人は次の日以降は安静にして誰かに感染しようとする動きがありますし、数日たてば症状も無くなり非感染者となるはずです。
だから数日後には数か月前に感染した人は非感染者となり別の人に感染をさせる恐れはないのですが、ここでは非常にシンプルなモデルを考えているため実現象とは違ってくると考えられます。
それに、毎日の日課みたいに「1日に絶対誰かを感染する」というルールなんてないですよね。
(1)式を微分して、単位日あたりの感染者数(新規感染者)について考えてみます。
\(N(t) = 2^{t+2}\)の微分ってちょっとやっかい(\(N(t) = (t+1)2^{t+1}\)とかしたらダメですよ)なのですが、丁寧にやりましょう。
いったん両辺に\(\log_e\)をとります。
\log_e N(t) &= &\log_e 2^{t+2}\\
&= &(t+2)\log_e 2\tag{2}
\end{align*}
こうしておいて両辺を\(t\)で微分します。
\frac{1}{N}\frac{dN}{dt} =\log_e 2
\end{align*}
ゆえに、(1)式の微分は、
\begin{align*}
\frac{dN}{dt} =\big(\log_e 2\big)N\tag{3}
\end{align*}
となります。
日あたりの感染者(新規感染者数)は、
その日までの総感染者数に比例するということを意味しています。
(3)式をもう少し一般的に書くと、
日あたりの感染者(新規感染者数)は、その日までの総感染者数に比例する
\begin{align*}
\frac{dN}{dt} =\frac{1}{a}N\tag{4}
\end{align*}
※後ほど説明しやすいように逆数で比例係数(\(1/a\))を表記しています。
\(a\):感染の緩和率(←このように名付けます)
この\(a\)が「外出禁止」や「電車通勤の禁止」などによって感染者の緩和させるパラメータになっています。
となります。
繰り返しになりますが、たった今僕らにできることは、
- 指数関数の期限を理解
- \(a\)を大きくする(\(a\)計画)
です。
ちょっと余談ですが、
\frac{dN}{dt} =\frac{1}{a}N\tag{4}
\end{align*}
これは、総感染者数\(N\)に関しての微分方程式ですので、「日あたりの感染者(新規感染者数)は、その日までの総感染者数に比例する」というとても当たり前の数理モデルから(4)式を立てることができますよね。
だとしたら、(4)式の微分方程式を解けば指数関数的増加を示すことがわかるはずです。
\frac{1}{N}dN &=\frac{1}{a}\,dt\\
\end{align*}
これを積分して・・・
\frac{1}{N}dN &=\frac{1}{a}\,dt\\
\log_e N &=\frac{1}{a} t+c\\
N&=Ce^{\frac{1}{a}t}\tag{5}
\end{align*}
となります。
\(N(0)=4\)だから
総感染者数\(N(t)\)は、
\begin{align*}
N&=4e^{\frac{t}{a}}\tag{6}
\end{align*}
となります。指数関数な増加です。
さらに余談を進めると・・・・
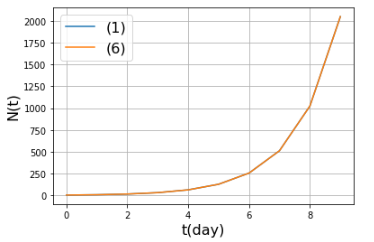
(1)式と(6)式は同じ数理モデルからスタートしたのに全然違う式になっていますね。
N(t) &=2^{t+2}\tag{1}\\
N(t)&=4e^{\frac{t}{a}}\tag{6}
\end{align*}
※\(\frac{1}{a}=\log_e 2\)
違うように見えますが、(1)(6)は同じ式を意味しています。
勉強のために(6)式の両辺に対数\(\log_2\)をとって「低の変換」を使って(1)式になるかどうかを確かめてみましょう。
まず対数をとります。
\log_2 N(t)&=2+ \frac{t}{a}\log_2 e
\end{align*}
底辺の変換公式はこれです。
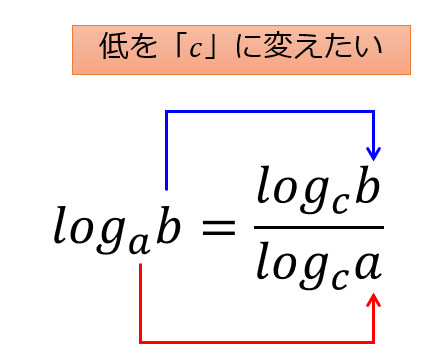

\(\frac{1}{a}=\log_e 2\)なので、\(\log_e 2=\frac{\log_e e}{\log_2 e}=\frac{1}{\log_2 e}\)
\log_2 N(t)&=2+ t
\end{align*}
よって、(6)式は、
N(t)=2^{t+2}
\end{align*}
となり、(6)式は(1)式と同じであることが確認できました。
グラフで重ねて書いてみても同じであることが確認できますね。
さらに、総感染者数\(N\)が指数関数的なのであれば、日あたりの感染者(新規感染者数)も指数関数的増加を示します。
なぜなら、日あたりの感染者は総感染者数\(N\)に比例している((4)式)からです。
日あたりの感染者数(新規感染者数)も指数関数的増加
\begin{align*}
\frac{dN}{dt} =\frac{4}{a}\,e^{\frac{t}{a}}\tag{7}
\end{align*}
※総感染者数に対しては比例ですが、時間に対しては比例じゃないですよ(;^ω^)
「日あたりの感染者(新規感染者数)も指数関数的増加」
👆これが今回の感染拡大の恐ろしさです!
このように感染者数が指数関数的な増加を示すことがおおよそ理解できたと思います。
感染症拡散の数理モデルはいろいろ考案されていますので一部紹介しておきます。
指数関数のは爆発的な増加なのか?
もう一つ指数関数でよく聞く表現があります。
以下のような表現です。
つまり、
指数関数は爆発的な増加だ!!
ってことです。
この記事の中では「めっちゃ感度よく増加する」ことを「爆発的な増加」って言うことにします。
ただこの「爆発的な増加」という表現はやや乱暴な気がしています。
- いったい何に対して爆発的な増加なのか?
- どれくらいの「爆発的」で人は「爆発的な増加」と感じるのか?
この2点について僕の考えを記そうと思います。
いったい何に対して爆発的な増加なのか?
(6)式の感染者数増加の数理モデルができたので、それを使って解説します。
N&=4e^{\frac{t}{a}}\tag{6}
\end{align*}
\(a\)という値を適当な値にしてグラフ化しました。
どれも指数関数ですが、これを見ると「爆発的な増加って何?」ってなりませんか?
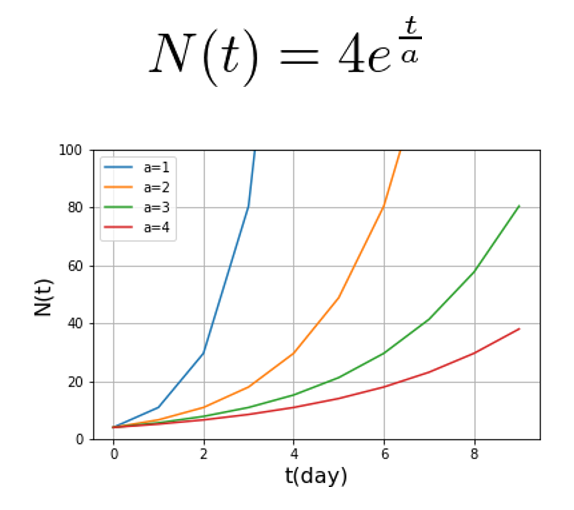

\(a=4\)だったらゆるやかな増加であるように見えますよね。
「爆発的に増加」というためには、何に対して爆発的な増加なのかを示さないといけません。
ここで考えるのは、関数の特徴的な幅です。
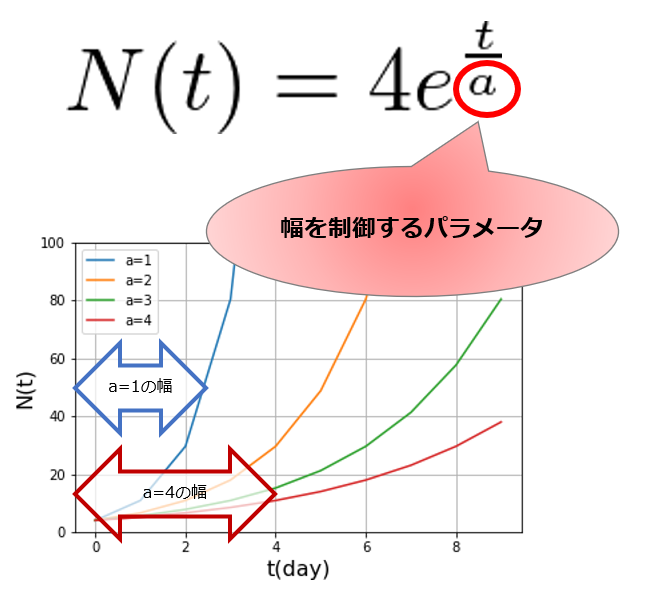

先ほど、\(a\):感染の緩和率
この\(a\)が「外出禁止」や「電車通勤の禁止」などによって感染者の緩和させるパラメータになっています。
と書きましたが\(a\)というパラメータはこの幅を決めているわけです。
この\(a\)が我々が日常で感じる時間よりも十分大きければ大した問題にはならないという事です。
「大した問題にならない」というのを言い換えると、「時間が十分あれば問題に対して対策を打てる」ってことです。
ただ・・・対策は絶対に打たないと、いくら緩和率が大きい(\(a\)が大きい)からと言って放置をしているとやがて増大しますよ(;^ω^)
横軸を100日までにして長い目で見たらこうなるんですから・・・


これで指数関数の増加の具合はつかめたのではないでしょうか?
どれくらいも「爆発的」具合で人は「爆発的な増加」と感じるのか?
これで「増加」の具合がわかったとして、
では人はどれくらいの「増加具合」でそれを「爆発的」と感じるのでしょうか?
人の体内のサイクルを考えてみましょう。
1秒、1分、1時間、1日、1週間、2週間、一ヶ月、3か月、半年、1年
どれですかね?
人の体内の周期は「太陽の日が出て、沈んで、また日が出て・・・」を繰り返しているので「1日周期」と考えるのが納得がいくのかと思います。
- 1時間ごとに気分が変わる人っていないですよね?
(たまにいるかもしれませんが・・・) - 1年間ずっと機嫌が悪い人っていないですよね?
(たまにいるかもしれませんが・・・)
ウイルスの感染者数報告も1日ごとでされています。
1年サイクルでの報告だと「まだやってたんか(笑)」となりますし、
2週間ごとだと「なんか久しぶりに聞いたな」って感じますよね。
つまり\(a\)が1(1日)に対して大きいかどうかを見れば良いわけです!!
\(a=1\)以上で指数関数が爆発的に増加するというわけではないですが、目安には使えます。
a=\frac{1}{\log_e 2}=1.44
\end{align*}
はい、約1.5です!!
\(a\)が1より大きい。
つまり、通常の”増える”という感覚の1.5倍の感覚くらいで指数関数(6)式は爆発的に増加するってことがわかりました。
どれだけ今コロナ感染の拡散がやばいか理解できましたでしょうか?
※補足
今回考えたのは、様々なありえないルールを課したときの感染者数増加の数理モデルです。
繰り返しになりますが、この記事の目的は「指数関数を理解しよう(^^)/」です。
感染者数増加の実現象を数理モデルで表すには、おそらくもっと複雑なモデルを考える必要があるでしょう。
指数関数を片対数グラフで表現すると?
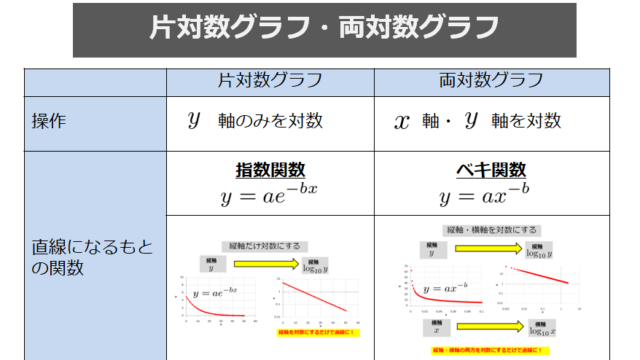
指数関数を表現するときに「片対数グラフ」を使います。
こちらの内容は下記の記事にまとめていますので是非どうぞ(^^)/
高校生でもわかるように丁寧に書きましたので是非お読みください。
上記の内容を一言で言ってしまうと、「縦軸を対数表記にすると直線になるよ」ってことです。
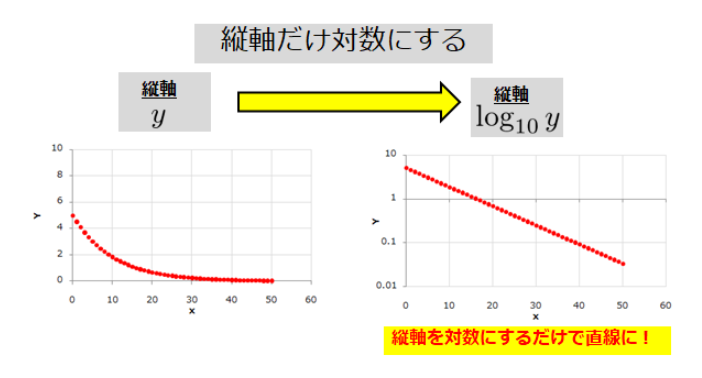

以上で、指数関数についての解説はおしまいです。
まとめ
今回は「指数関数」についても3つの特徴について解説しました。
- どのような時に指数関数増加になるのか?
- 指数関数は爆発的な増加なのか?
- 指数関数を片対数グラフで表現すると?
- 日あたりの感染者(新規感染者数)は、その日までの総感染者数に比例する
\begin{align*}
\frac{dN}{dt} =\frac{1}{a}N\tag{4}
\end{align*}
\(a\):感染の緩和率
この\(a\)が「外出禁止」や「電車通勤の禁止」などによって感染者の緩和させるパラメータ
この微分方程式から、
感染者数\(N(t)\)は、
\begin{align*}
N&=4e^{\frac{t}{a}}\tag{6}
\end{align*}
※後ほど説明しやすいように逆数で比例係数(\(1/a\))を表記しています。
- \(a\)が1(1日)にたいして大きいかどうかを見れば指数関数が爆発的な増加を示すかがわかる。
- 指数関数は「縦軸を対数表記にすると直線になる