こんにちは(@t_kun_kamakiri)。
本日は、「1次元のバーガース方程式」の一般解のお話をします。
前回の記事までで、「1次元の移流方程式」「1次元の拡散方程式」「1次元バーガース方程式」をPythonで実装するというのをやりました。
バーガース方程式の理解には「拡散方程式」の一般解と関係しているので、そちらの記事を読んでいることが前提となります。
本件の基本的な内容はこちらのサイトにそってやっていきます。
この記事ではこんな人を対象にしています。
- Pythonを使い始めたけどどう使うかわからない
- 流体の数値計算をはじめて勉強する人
- 一次元のバーガース方程式は、コール・ホップ変換により拡散方程式になる(導出過程を載せます)
- 一次元のバーガース方程式の一般解
バーガース方程式とは
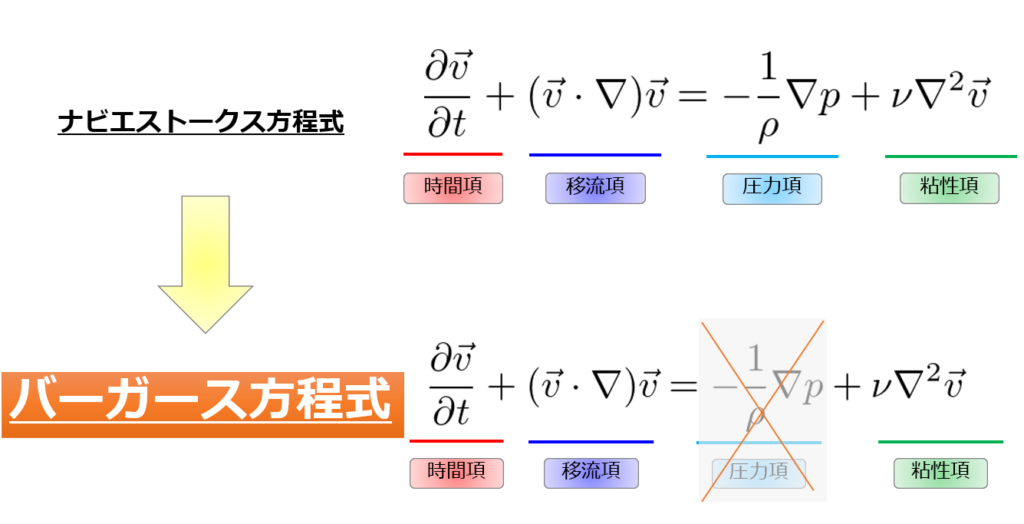
バーガース方程式は、ナビエストークス方程式において移流項が圧力項より十分大きい場合\(|(\boldsymbol{u}\cdot\nabla)\boldsymbol{u}|>>|\frac{1}{\rho}\nabla p|\)において近似される以下の式で記述されます。
1次元のバーガース方程式
\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}= \nu \frac{\partial^2 u}{\partial x^2} \tag{1}
\end{align*}
圧力項より移流項の方が十分大きいとは、例えば流速がものすごく大きい極音速領域や流速の空間変動が急激な場合などが考えられます。
ここからいくつかバーガース方程式の特徴を以下に列挙します。
本記事のメインの内容は「コール・ホップ変換」についてですね(^^)/
というわけで、さっそくコール・ホップ変換について見ていきましょう。
コール・ホップ変換
以下のバーガース方程式、
\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}= \nu \frac{\partial^2 u}{\partial x^2}\tag{1}
\end{align*}
の解である\(u\)を\(\phi\)を用いて以下のように変換すると・・・
u &= -2\nu\frac{\partial }{\partial x}\log\phi \\
&or \\
u &= -2\nu\frac{1}{\phi}\frac{\partial \phi}{\partial x}\tag{2}
\end{align*}
\(phi\)が従う方程式は、1次元の拡散方程式に変換されます。
\frac{\partial \phi}{\partial t}= \nu \frac{\partial^2 \phi}{\partial x^2}\tag{3}
\end{align*}
これがコール・ホップ変換です。
そして(3)式は一般解が存在し、
\phi(x,t)=\frac{1}{\sqrt{4\pi\nu t}}\int^{\infty}_{-\infty}e^{-\frac{(x-s)^2}{4\nu t}}\phi_0(s)ds\tag{4}
\end{align*}
となります。
※\(\phi_0\)は初期状態です。
一般解\(\phi\)が求まるのであれば、(2)式を使うことでバーガース方程式の一般解\(u\)も求まるというわけです。
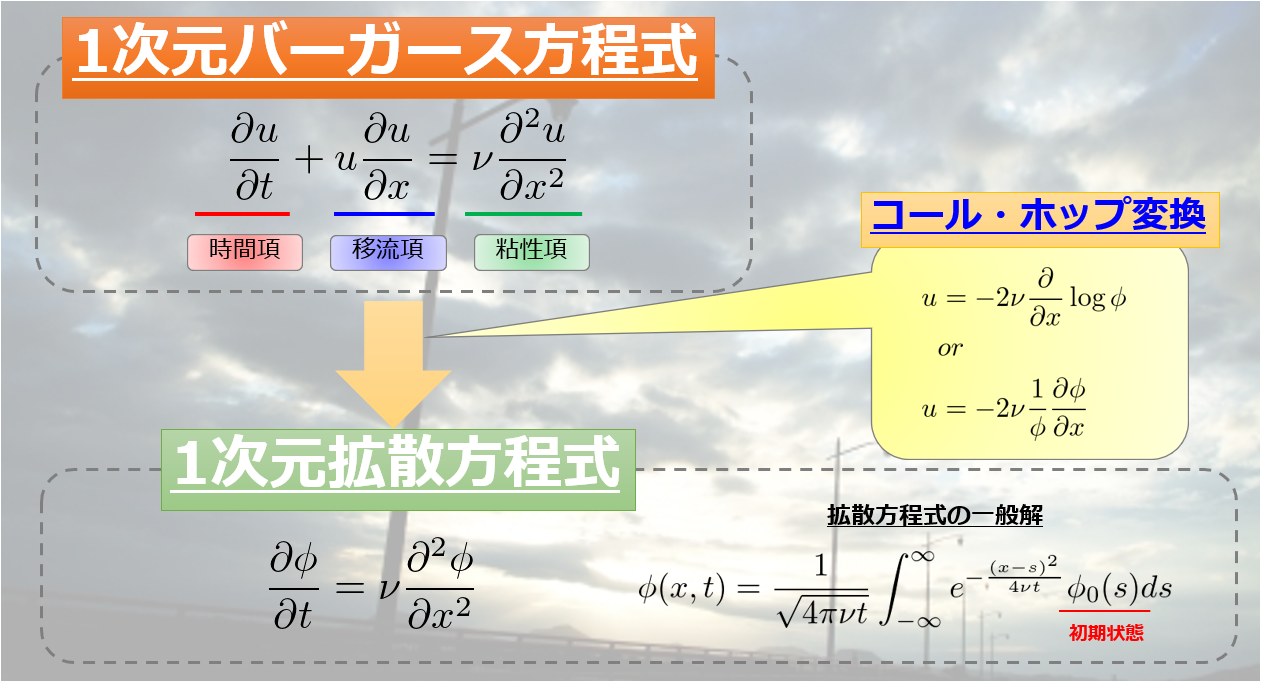
繰り返しになりますが、それを絵にまとめたのが☟こちらです。
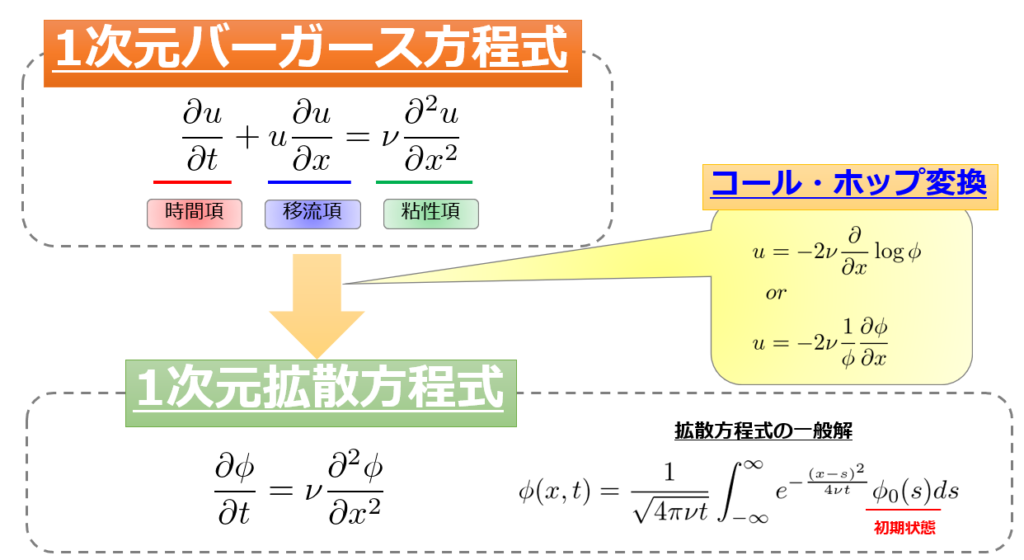


それを以下で確かめたいと思います。
確認!バーガース方程式をコール・ホップ変換をすることで1次元拡散方程式に変換される
再び、1次元バーガース方程式を持ってきます。
\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}= \nu \frac{\partial^2 u}{\partial x^2}\tag{1}
\end{align*}
これを計算しやすいように、左辺第二項を\(u\frac{\partial u}{\partial x}=\frac{\partial }{\partial x}\big(\frac{u^2}{2}\big)\)となることを用いて、それを右辺にまとめてやります。
\frac{\partial u}{\partial t}= \frac{\partial }{\partial x}\bigg(-\frac{u^2}{2}+\nu \frac{\partial u}{\partial x}\bigg)\tag{5}
\end{align*}
これでちょっとすっきりしました。
では、各項を\(u =-2\nu\frac{\partial }{\partial x}\log\phi = -2\nu\frac{1}{\phi}\frac{\partial \phi}{\partial x}\)の変換をしてみましょう。
左辺
\frac{\partial u}{\partial t}&=-2\nu\frac{\partial }{\partial t}\frac{\partial }{\partial x}\log\phi\\
&\underset{tとxの微分\\の順序を\\入れ替え}=-2\nu\frac{\partial }{\partial x}\frac{\partial }{\partial t}\log\phi\\
&=-2\nu\frac{\partial }{\partial x}\bigg(\frac{1}{\phi}\frac{\partial \phi}{\partial t}\bigg)\tag{6}
\end{align*}
※\(x\)と\(t\)の微分の入れ替えは行ってもいいの?って思う人もいるかもしれませんが、それはこちらの記事をお読みください。
\(\frac{\partial^2 u}{\partial x \partial t}\)と\(\frac{\partial^2 u}{\partial t\partial x}\)が存在して、それぞれ連続ならば\(\frac{\partial^2 u}{\partial x\partial t}=\frac{\partial^2 u}{\partial t\partial x}\)。入れ替えはOK。
右辺
\frac{\partial }{\partial x}\bigg(\frac{u^2}{2}+\nu \frac{\partial u}{\partial x}\bigg)&=\frac{\partial }{\partial x}\left \{-2\nu^2\frac{1}{\phi^2}\bigg(\frac{\partial \phi}{\partial x}\bigg)^2-2\nu^2 \frac{\partial }{\partial x}\bigg(\frac{1}{\phi}\frac{\partial \phi}{\partial x}\bigg)\right \}\\
&\underset{第二項は\\商の微分}=-2\nu^2\left \{ \frac{1}{\phi^2}\bigg(\frac{\partial \phi}{\partial x}\bigg)^2+\frac{\frac{\partial^2\phi}{\partial x^2}-\bigg(\frac{\partial \phi}{\partial x}\bigg)^2}{\phi^2}\right \}\\
&=-2\nu^2\frac{\partial}{\partial x}\bigg(\frac{\frac{\partial^2\phi}{\partial x^2}}{\phi}\bigg)\tag{7}
\end{align*}
(6)(7)をまとめると以下のようになります。
\frac{\partial}{\partial x}\frac{1}{\phi}\left \{ \frac{\partial \phi}{\partial t}-\nu\frac{\partial^2 \phi}{\partial x^2}\right \}=0
\end{align*}
よって、これを積分すると・・・
\frac{\partial \phi}{\partial t}=\nu\frac{\partial^2 \phi}{\partial x^2}\tag{8}
\end{align*}
となります。
※任意定数を付けても良いですが、線形の方程式なので\(\phi\)を適当に定数倍足すことで定数は消えるので書いても書かなくても同じことです。
というわけで、「1次元バーガース方程式」をコール・ホップ変換することで拡散方程式になりましたね(^^)/
そして、(8)式「1次元拡散方程式」の一般解は以下となることが解析的に求まります。
\phi(x,t)=\frac{1}{\sqrt{4\pi\nu t}}\int^{\infty}_{-\infty}e^{-\frac{(x-s)^2}{4\nu t}}\phi_0(s)ds\tag{4}
\end{align*}
※導出過程はネット上の記事でよく見かけるのでそちらに譲ることにしましょう。
例えば、こちらの記事がわかりやすいかと思います。
ということは・・・\(u =-2\nu\frac{\partial }{\partial x}\log\phi\)なので、
バーガース方程式の一般解は以下のようになることがわかりますね!
u (x,t)=-2\nu\frac{\partial }{\partial x}\log\left \{\frac{1}{\sqrt{4\pi\nu t}}\int^{\infty}_{-\infty}e^{-\frac{(x-s)^2}{4\nu t}}\phi_0(s)ds \right \}\tag{9}
\end{align*}
これで、1次元バーガース方程式の一般解が求まりました(^^)/
でも、(9)式の積分が解析的に実行できるかどうかは初期状態\(\phi_0\)に依ります。\(\phi_0\)が複雑な関数だったら積分ができないということになります。
なので、実際は「1次元のバーガース方程式」を数値計算して解の振る舞いを求めることが多いかと思いますね。
まとめ
少々計算が複雑になりましたが、
「1次元バーガース方程式」をコール・ホップ変換をすることで「1次元拡散方程式」に変換することができました。
再び絵に書くと、☟これです。
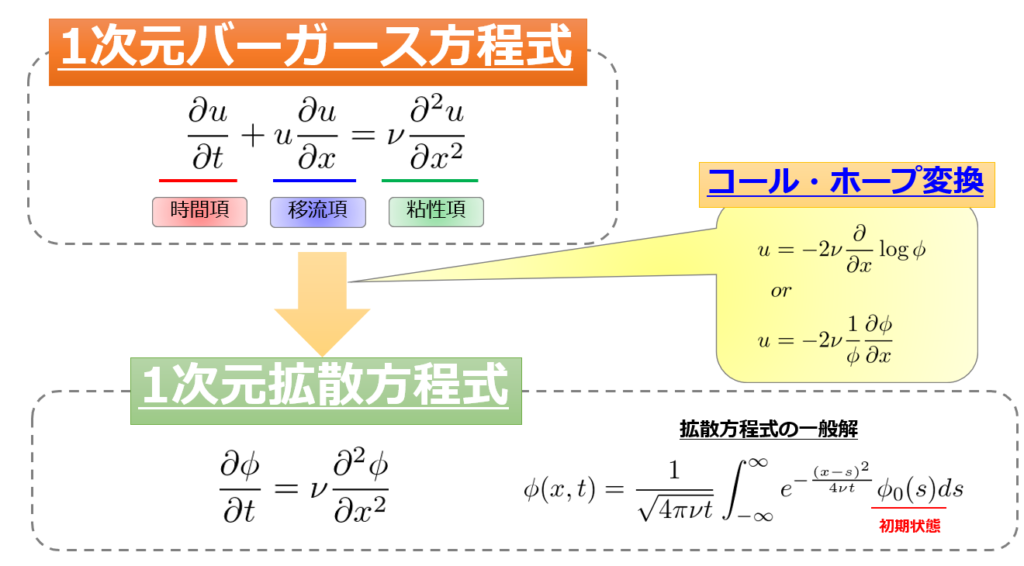

\(u =-2\nu\frac{\partial }{\partial x}\log\phi\)なので、
バーガース方程式の一般解は以下となります。
バーガース方程式の一般解
u (x,t)=-2\nu\frac{\partial }{\partial x}\log\left \{\frac{1}{\sqrt{4\pi\nu t}}\int^{\infty}_{-\infty}e^{-\frac{(x-s)^2}{4\nu t}}\phi_0(s)ds \right \}\tag{9}
\end{align*}
今回は、1次元バーガース方程式の特徴のひとつである「コール・ホップ変換」について解説しましたが、バーガース方程式は非線形方程式ゆえにまだまだ色々な特徴が知られており、とても奥が深いです。
☟以下の書籍で詳しく書かれているので是非お読みください(‘◇’)ゞ