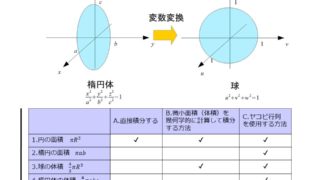
こちらの記事で円の面積、楕円の面積、球の体積、楕円体の体積などを求めましたが、一般的な\(n\)次元空間の球の体積はどのように書けるかご存知でしょうか?
前回の記事はこちら
本記事は、\(n\)次元空間の球の体積を紹介したいと思います。
n次元空間の半径Rの球の体積
\begin{align*}V_{n}=\frac{2\pi^{n/2}}{n\Gamma(n/2)}R^{n}\cdot\cdot\cdot (\diamondsuit)\end{align*}
そもそもどうして\(n\)次元の球の体積も求めるのか?
だいたい\(n\)次元空間の球の体積を求めてどうしたいのだと・・・・・そう思われる方がいるかと思います。
実際我々が住んでいる実空間は3次元で記述できるので、大きく見ても3次元空間の球の体積、つまり\(\frac{4}{3}\pi R^3\)だけで十分かもしれません。
しかし、解析力学でも統計力学でも運動を記述するのに、位相空間(座標と運動量を使った空間)を使うことがあります。
その時、\(n\)個の粒子の運動については、座標で\(3n\)次元、運動量で\(3n\)次元なので合計\(6n\)次元になり、こういった位相空間で、
\begin{align*}\int\int\cdot\cdot\cdot \int\int dx_{1}dx_{2}\cdot\cdot\cdot dx_{3n}dp_{1}dp_{2}\cdot\cdot\cdot dp_{3n}\cdot\cdot\cdot (1)\end{align*}
を計算する場合が出てきます。
特に統計力学の分配関数\(Z\)を計算するときです。
>分配関数
そういったときに、特別\(x_{i}\)、\(p_{i}\)にも特別な方向がなく等方的であれば、次元が\(6n\)次元であろうと(1)式を計算する必要性に迫られます。
しかし、”特別\(x_{i}\)、\(p_{i}\)にも特別な方向がなく等方的であれば”割と簡単に求めることができます。その時の公式として\(n\)次元の半径\(R\)の球の体積(\(\diamondsuit\))を求めておくと(知っておくと)非常に便利なのです。
数学的帰納法で\(n\)次元の球の体積を求めることができるか?
例えば、
円の面積は、
\begin{align*}\pi R^2\cdot\cdot\cdot (2)\end{align*}
球の体積は、
\begin{align*}\frac{4}{3}\pi R^3\cdot\cdot\cdot (3)\end{align*}
であるので、この(2)と(3)からもっと次元を増やしていってある規則を見いだせれば、きっと\(n\)次元の半径\(R\)の球の体積は”こうに違いない”と仮説を立てて、数学的帰納法で「ほらね♪」って決めたいところですが・・・・
これ以上の次元の体積ってご存知だろうか?(笑)
4次元の球の体積って聞いたことないのですが(少なくとも僕は・・・)
だから、数学的帰納法で導くことは断念します。
\(n\)次元の半径\(R\)の球の体積を求める
球なので、極座標を考えているものとしましょう。
まず半径\(R\)の球の体積は、
\begin{align*}V_{n}(R)=a_{n}R^{n}\cdot\cdot\cdot (4)\end{align*}
と書けるとします。
ここでの、目標はいかにして\(a_{n}\)を求めるかです。
半径が、
\begin{align*}r^2=r_{1}^2+r_{2}^2+r_{3}^2\cdot\cdot\cdot +r_{n}^2\cdot\cdot\cdot (5)\end{align*}
です。
ところで、\(r+dr ~ r\)までの球殻の体積\(dV_{n}\)というのは、(4)式を微分することにより、
\begin{align*}dV_{n}=na_{n}r^{n-1}\cdot\cdot\cdot (6)\end{align*}
と求まります。
(5)(6)式は後ほど使います。
本当は、こう求めた方がわかりやすいかもしれません。
\begin{align*}dV_{n}=V_{n}(r+dr)-V_{n}(r)=a_{n}(r+dr)^{n}-a_{n}r^{n}\end{align*}
ところで、
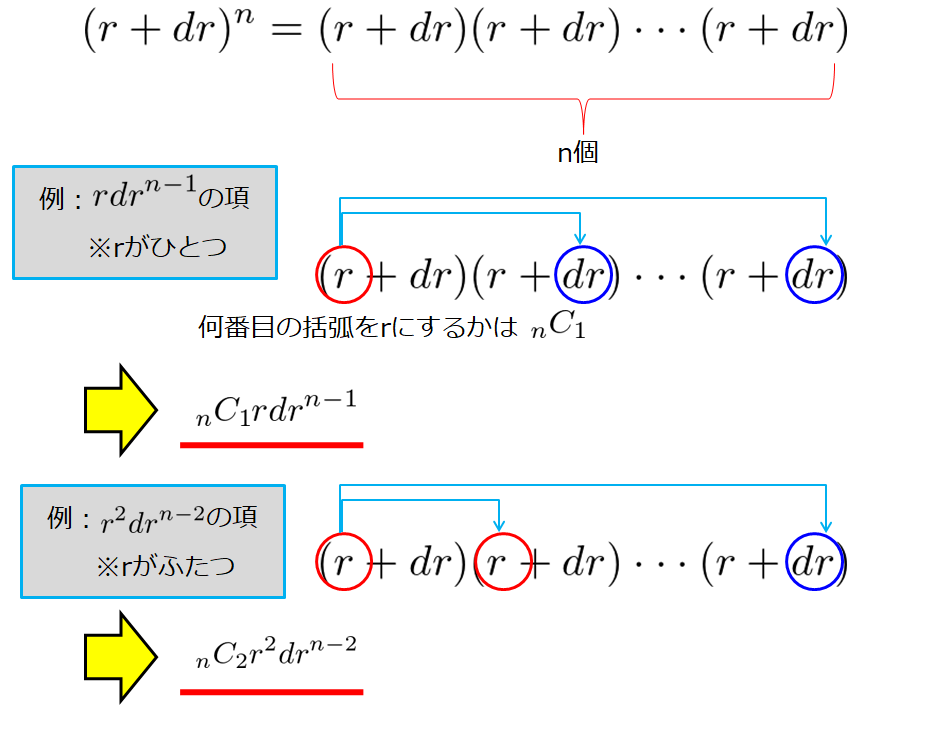
\((r+dr)^{n}\)は、\((r+dr)\)を\(n\)回掛け算したものだから、
\begin{align*}(r+dr)^{n}=(r+dr)(r+dr)\cdot\cdot\cdot (r+dr)\end{align*}
となります。
これは、何番目の括弧の\(r\)を\(k\)回使って、残り\(n-k\)回は\(dr\)を使って掛け算の形を作る場合に相当します。
なので、
\begin{align*}(r+dr)^n=\sum_{k}^{n} {}_{n}C_{k}r^{k}dr^{n-k}\end{align*}
となります。
※具体例を示しておきましょう。

このように、足していけば\((r+dr)^n=\sum_{k}^{n} {}_{n}C_{k}r^{k}dr^{n-k}\)となることが理解できます。
ですが、和を全部使うのではなく\(dr\)は微小なので2次の項までとるとすると、
\(k=n\)と\(k=n-1\)の場合しか残りません。
\begin{align*}(r+dr)^n=\sum_{k}^{n} {}_{n}C_{k}r^{k}dr^{n-k}\sim {}_{n}C_{n}r^{n}+{}_{n}C_{n-1}r^{n-1}dr\end{align*}
だから、
\begin{align*}dV_{n}=V_{n}(r+dr)-V_{n}(r)=a_{n}(r+dr)^{n}-a_{n}r^{n}=na_{n}r^{n-1}dr\end{align*}
となります。
ここで唐突ですが・・・・
\begin{align*}I=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\cdot\cdot\cdot \int_{-\infty}^{\infty}e^{-(r_{1}^2+r_{2}^2+\cdot\cdot\cdot +r_{n}^2)}\, \,\,\,\,\,dr_{1}dr_{2}\cdot\cdot\cdot dr_{n}\cdot\cdot\cdot (7)\end{align*}
というのを2通りの方法で求めたいと思います。
これは、\(a_{n}\)を求めるのに使います。
方法1
(7)式は、
\begin{align*}\int_{-\infty}^{\infty}e^{-r_{1}^2}\, dr_{1}=\sqrt{\pi}\cdot\cdot\cdot (8)\end{align*}
を単純に\(n\)回かけているものであるとみることができます。
だから、
\begin{align*}I=\bigg(\int_{-\infty}^{\infty}e^{-r_{1}^2}\, dr_{1}\bigg)^{n}=\bigg(\sqrt{\pi}\bigg)^{n}\cdot\cdot\cdot (9)\end{align*}
となります。
この結果を覚えておくとして・・・・
方法2
(7)式の指数部分は(5)式を使い、(7)式の微小体積部分は(6)式を使うと、
\begin{align*}I=\int_{0}^{\infty}e^{-r^2}a_{n}nr^{n-1}dr\cdot\cdot\cdot (10)\end{align*}
これを頑張って計算するのではなく、ガンマ関数の定義を使って表記します。
ガンマ関数
\begin{align*}\Gamma(n)=\int_{0}^{\infty}t^{n-1}e^{-t}dt\end{align*}
※覚えにくいですが、これを使うと便利な数学公式を用いて値自体はわかるので(11)式をガンマ関数を使って表記することを試みましょう。
(10)式をガンマ関数の形にするのには、置換積分\(r^2=t\)とすれば良いです。
微分すると\(2rdr=dt\)であり、積分区間は\(t\)になっても変わらないので、
\begin{align*}I=a_{n}n\int_{0}^{\infty}e^{-t}t^{\frac{n}{2}-1}dr=\frac{1}{2}na_{n}\Gamma(\frac{n}{2})\cdot\cdot\cdot (11)\end{align*}
※途中計算は省略します。
(9)式と(11)式を見比べると・・・
\begin{align*}I=\bigg(\sqrt{\pi}\bigg)^{n}\cdot\cdot\cdot (9)\end{align*}
\begin{align*}I=\frac{1}{2}na_{n}\Gamma(\frac{n}{2})\cdot\cdot\cdot (11)\end{align*}
このようにもともと同じ式を計算したのですから、
\begin{align*}\bigg(\sqrt{\pi}\bigg)^{n}=\frac{1}{2}na_{n}\Gamma(\frac{n}{2})\end{align*}
となり、
\begin{align*}a_{n}=\frac{\pi^{\frac{n}{2}}}{n\Gamma(\frac{n}{2})}\cdot\cdot\cdot (12)\end{align*}
今一度、目標は何であったかを確認すると、\(a_{n}\)を求めることでしたね。
というわけで、(12)式を(4)式に代入すれば
ここにボックスタイトルを入力
\begin{align*}V_{n}=\frac{2\pi^{n/2}}{n\Gamma(n/2)}R^{n}\cdot\cdot\cdot (\diamondsuit)\end{align*}
となります。
一応確認
(\(\diamondsuit\))が\(n\)次元の半径\(R\)の球の体積を求める一般公式であるならば、
\(n=2\)の時は、面積の公式\(\pi R^2\)
\(n=3\)の時は、面積の公式\(\frac{4}{3}\pi R^3\)
になっています。
これはご興味がある方は、(n=2,n=3)の時のガンマ関数の値を調べて計算して確かめてみてください(^^)/