気体の状態方程式とは何か?と問われたら真っ先に思いつくのが、
\end{align*}
ではないでしょうか。
しかし、これは気体の状態方程式の中でも「理想気体の状態方程式」と言われているもので、すべての気体が\(pV=nRT\)に従うとは限りません。
本記事
理想気体として扱えない場合はどうすれば良いかというお話をします。
※実在気体で使う状態方程式はどのようなものがあるのかな?
”理想”気体の状態方程式というのは下記の記事にも書きましたので参考にしてください。
pV=nRT
\end{align*}
さらに\(pV=nRT\)だと単一気体の理想気体の状態方程式なので、「混合気体の場合」は下記のような記事の内容になるのです。
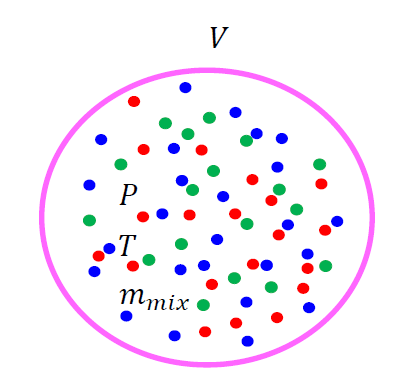
気体の状態方程式
「理想」という言葉を取って、単に気体の状態方程式としてみましょう。
理想気体として扱えない場合はどうすれば良いかというのを紹介したいと思います。
簡単のために1モルあたりの気体を考え、その体積を\(v\)と置くことにします。
ビリアル展開
理想気体の状態方程式を次のように修正する。
\frac{pv}{RT}=1+\frac{b_{2}(T)}{v}+\frac{b_{2}(T)}{v^2}+\cdot\cdot\cdot (1)\end{align*}
難しく考えると、難しく感じるものであるが、これは単に第一項までなら「理想気体の状態方程式」であるが、実際の気体はそこから幾分かずれているだろうと考えて、第二項以降を足しているだけです。
\(b_{2},b_{3}(T)・・・\)などは、ビリアル係数と言い、気体の種類によって異ります。
ビリアル係数\(b_{i}\)に比べて体積\(v\)が大きい場合は、(1)式の右辺は第一項のみとなり、やはり「理想気体の状態方程式」に帰着します。
このように、実在気体は「理想気体の状態方程式」から幾分かずれるのです。
だから、実在気体を正確に表現するために、幾つか状態方程式が提案されていますが、今回はその中でも最も有名なのが「ファン・デル・ワールスの状態方程式」のみ紹介しておきましょう。
ファン・デル・ワールスの状態方程式
1モルの気体に対して、ファン・デル・ワールスの状態方程式は、
(p+\frac{a}{v^2})(v-b)=RT\cdot\cdot\cdot (2)
\end{align*}
と書きます。
これは次のようにして理解することができます。
理想気体の状態方程式(1)式をまず考えます。
pv=RT
\end{align*}
これは分子を大きさのない質点だと考えていたので、実際は分子の容量は\(b\)あるのだよってことを加えればよいので、
p(v-nb)=RT
\end{align*}
ここで、分子間力が働く場合は、どのように変更が加えられるでしょうか?
理想気体の場合は、壁に与える力が圧力\(p\)として書かれていましたが、分子間力で分子同士が引き合っていると、実際の圧力\({P}’\)は理想気体の圧力\(p\)より減っているでしょう。
では、どれくらい減るのでしょうか?
分子の単位体積当たりの数\(\frac{n}{v}\)の分だけ比例して減りそうですね。
数と言っても、本当の数は「\(n\)×アボガドロ数」だがアボガドロ数は定数として考えているので無視します。
今は1モルあたりで考えているので、\(\frac{1}{v}\)の分だけ比例して減りそうであるということがわかりました。
さらに、分子間力は相手があっての分子間力なので、\(\frac{1}{v}\)に比例するのではなくて、\(\frac{1}{v}\times \frac{1}{v}=\big(\frac{1}{v}\big)^2\)という形で比例することになります。
比例定数を\(a\)とおくと、実際の圧力は、
{p}’=p-a \big(\frac{1}{v}\big)^2
\end{align*}
と、このように書けます。
よって、ファンデルワールスの状態方程式は、理想気体の状態方程式から補正されて、
ファンデルワールスの状態方程式
\big({p}’+\frac{a}{v^2}\big)\big(v-b \big)=RT
\end{align*}
⇔あるいは
{p}’=\frac{RT}{v-b}-\frac{a}{v^2}
\end{align*}
と書けます。
ここで\({p}’\)を\(p\)と書けば、
\big(p+\frac{a}{v^2}\big)\big(v-b \big)=RT\cdot\cdot\cdot (3)
\end{align*}
⇔あるいは
p=\frac{RT}{v-b}-\frac{a}{v^2}\cdot\cdot\cdot (4)
\end{align*}
となります。
さて、内部の状態に対する基礎的な方程式を得ることができました。
内部の状態(内部エネルギー)のまとめ
熱力学的な状態関数は、
f(P,T,V)=0\cdot\cdot\cdot (5)
\end{align*}
として関係式が成り立ちます。
理想気体の場合
pV=nRT\cdot\cdot\cdot (6)
\end{align*}
理想気体でない場合(ファン・デル・ワールスの状態方程式)
p=\frac{RT}{v-b}-\frac{a}{v^2}\cdot\cdot\cdot (7)
\end{align*}
気体についてはこの2つを覚えておくとだいたい良いだろう。