【簡単にできた！】データをPythonで読み込んでアニメーション作成

こんにちは（@t_kun_kamakiri）(‘◇’)ゞ

偏微分方程式を数値計算で解いて、結果をアニメーションしたいと思ったときにPythonを使うと楽でしたので記事に残しておこうと思います(^^)/

本記事の内容

Fortranで出した出力データをPythonでアニメーション作成する

前回の記事で、アニメーション作成にはgnuplotやparaviewを使ったりしました。

（前回の記事）Fortranで数値計算→gnuplotのスクリプトを使ってアニメーション作成
Fortranからgnuplotを使って1次元グラフのアニメーション作成
 Fortranからgnuplotを使って3次元アニメーション作成
 1次元の移流方程式を前進差分、後退差分、中心差分で解く。【Fortranコードあり】
（前回の記事）Fortranで数値計算→paraviewでvtkファイルを読み込みアニメーション作成
Fortranで解いた問題をParaviewを使ってvtkでアニメーション作成
（前回の記事）Pythonで数値計算してPythonでアニメーション作成
Pythonで2次元の熱伝導方程式をアニメーションが簡単にできた

色々試してみて・・・・

Fortranで数値計算してデータを出力しておいて、Pythonでサクッっとアニメーション作成作れるようにもしておこうかなって思いました。

【本記事の内容】数値計算からアニメーション作成までのフローはこちら↓。

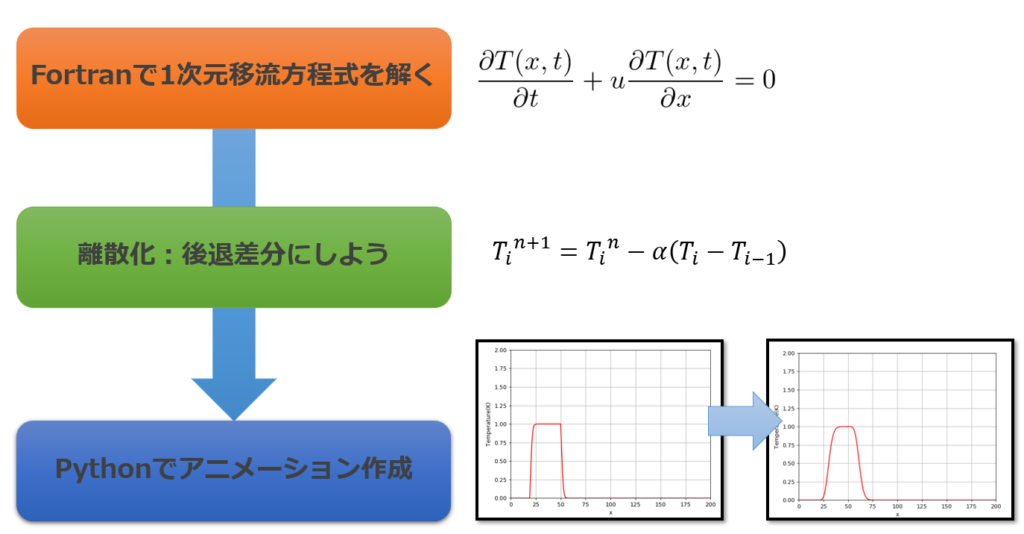
※Fortranのコードとスクリプトは本記事にアップされています。
※FortranのコードはFortran90/95の書き方にしているつもりですが正確に書けているかは不明です。
※FortranはWSLを使ってインストールしています。
※PythonはJupyter Notebookを使っています。

解く方程式は1次元移流方程式
1次元移流方程式を離散化する
Fortranで1次元移流方程式を解く
Pythonでアニメーション作成
1次元移流方程式のアニメーション結果
参考書

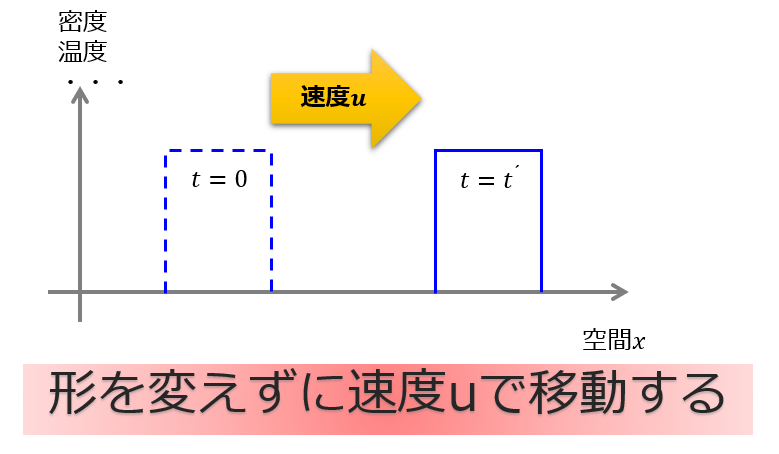
解く方程式は1次元移流方程式

簡単な偏微分方程式を題材にしておきます(^^)

１次元の移流方程式

\begin{align*}\frac{\partial T(x,t)}{\partial t}+u\frac{\partial T(x,t)}{\partial x}=0\tag{1}\end{align*}

※\(u\)：一定速度

1次元の移流方程式は、下記の絵のように何かの物理量を形を変えずに一定速度\(u\)で運ぶ方程式を意味しています。

1次元移流方程式を離散化する

(1)式を離散化する場合は注意する必要があったんですよね。

1次元移流方程式を陽解法で解くときには、数値的に安定な条件で離散化&条件設定をする必要がありました。

前回の記事はこちら

1次元の移流方程式を前進差分、後退差分、中心差分で解く。【Fortranコードあり】

カマキリ

この記事は、なかなか教育的な記事が書けた気がする。

結論を書いておくと、

陽解法で解くのあれば後退差分（風上差分）でないと数値的に安定には解いてくれないということがわかりました。

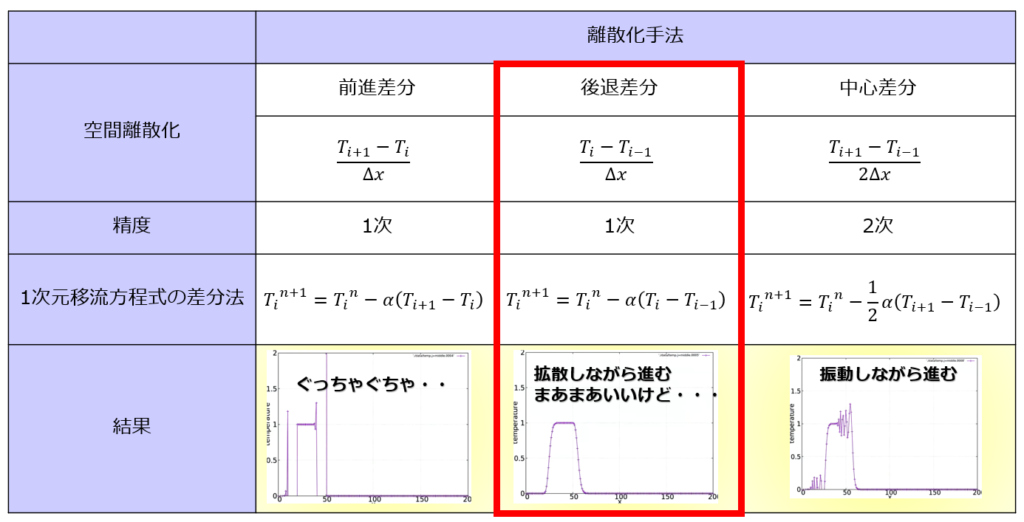
↑Fortranで解くのは赤枠の離散化した式です。
※\(\alpha=\frac{u\Delta t}{\Delta x}\)

さらに、

空間と時間の刻みにも制限がありました。
（記事の内容は1次元移流方程式ではありませんが・・・）

1次元熱伝導方程式の陽解法で解いた時の数値的安定性

話をまとめると・・・

離散化する際の差分に注意する
数値的に安定な「空間と時間」の刻みを考える

※陰解法で解く場合はまた状況が異なりますが・・・(‘_’)

Fortranで1次元移流方程式を解く

Fortranのコードを載せておきましょう(^^)/

module constants
  implicit none
  integer::i,nt
  integer, parameter :: imax = 200,ntmax = 250
  real(8):: T(0:imax),xmax,x,u,dx,dt,cfl
  integer,parameter :: SP = kind(1.0)
  integer,parameter :: DP = selected_real_kind(2*precision(1.0_SP))
end module constants

module print
  use constants
  implicit none
 
 contains
  subroutine print__profile(f)
    real(DP), dimension(0:imax), intent(in) :: f
    integer :: counter = 0
    character(len=*), parameter :: base = "./data/temp.j=middle."
    character(len=4) :: serial_num
    character(len=40) filename
  
    write(serial_num,'(i4.4)') counter

    write(filename,"(a,i5.5,a)") base//serial_num
    open(10,file=filename)
    do i = 0 , imax
       write(10,*) i*dx, f(i)
    end do
    close(10)
    counter = counter + 1
    
  end subroutine print__profile
end module print

program thermal_explicit
  use constants
  use print

  implicit none
  
  u=1
  dt   = 0.1
  xmax = 200
  dx   = xmax/imax
  cfl=u*dt/dx
  
  open(10,file="initial.txt")
  open(11,file="final.txt")

   !initial state
   do i = 0, imax
      x = dx*i
      if (i>=20 .and. i<=50) then
         T(i) = 1
       else
         T(i) =0
      endif
      write(10,*) i,x,T(i)
   enddo
   call print__profile(T(:))

   
   !Time step
   do nt = 1, ntmax
      do i = 1, imax-1
         T(i) = T(i) -cfl*(T(i+1)-T(i))
      end do
      if (mod(nt,10)==0) call print__profile(T(:))
      write(*,*)nt
   end do
   
   !Final state
   do i = 0, imax
      x = dx*i
      write(11,*) i,x,T(i)
   end do
end program thermal_explicit

module constants

implicit none

integer::i,nt

integer, parameter :: imax = 200,ntmax = 250

real(8):: T(0:imax),xmax,x,u,dx,dt,cfl

integer,parameter :: SP = kind(1.0)

integer,parameter :: DP = selected_real_kind(2*precision(1.0_SP))

end module constants

module print

use constants

implicit none

contains

subroutine print__profile(f)

real(DP), dimension(0:imax), intent(in) :: f

integer :: counter = 0

character(len=*), parameter :: base = "./data/temp.j=middle."

character(len=4) :: serial_num

character(len=40) filename

write(serial_num,'(i4.4)') counter

write(filename,"(a,i5.5,a)") base//serial_num

open(10,file=filename)

do i = 0 , imax

write(10,*) i*dx, f(i)

end do

close(10)

counter = counter + 1

end subroutine print__profile

end module print

program thermal_explicit

use constants

use print

implicit none

u=1

dt = 0.1

xmax = 200

dx = xmax/imax

cfl=u*dt/dx

open(10,file="initial.txt")

open(11,file="final.txt")

!initial state

do i = 0, imax

x = dx*i

if (i>=20 .and. i<=50) then

T(i) = 1

else

T(i) =0

endif

write(10,*) i,x,T(i)

enddo

call print__profile(T(:))

!Time step

do nt = 1, ntmax

do i = 1, imax-1

T(i) = T(i) -cfl*(T(i+1)-T(i))

end do

if (mod(nt,10)==0) call print__profile(T(:))

write(*,*)nt

end do

!Final state

do i = 0, imax

x = dx*i

write(11,*) i,x,T(i)

end do

end program thermal_explicit

ファイルの書き出し部分の解説↓

Fortranを実行すると・・・（僕はgfortranを使っています）

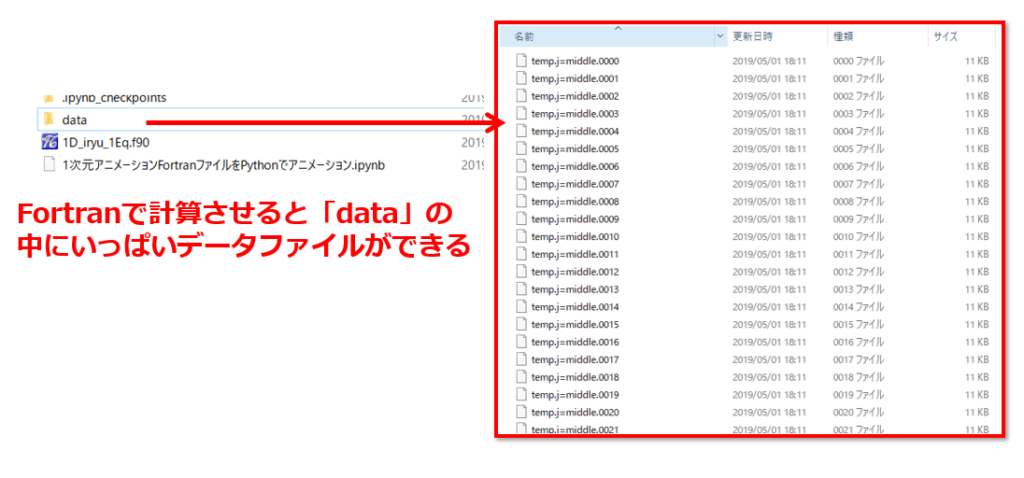
データがいっぱいできるので、これをPythonでアニメーション作成しようということになります。

Pythonでアニメーション作成

Pythonでのアニメーション作成用のコードはこちら↓

%matplotlib nbagg
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import os

#データのパスを取得
path=os.getcwd()+'\data'

#「data」ディレクトリ内のファイルリスト（フォルダも含む）
folder_files=os.listdir(path) 

#ファイルのみ取得する（フォルダを含む場合はフォルダは除く）
files=[]
for filename in os.listdir(path):
    if os.path.isfile(os.path.join(path, filename)): #ファイルのみ取得
        files.append(filename)


file_count=len(files)

def graph(a,f,x_label,y_label,title):
    plt.plot(a,f)
    plt.grid()
    plt.title(title)
    plt.xlabel(x_label)
    plt.ylabel(y_label)
    plt.show()

#initial state
nstep100='0000'
#data=np.loadtxt('./data/old/test.0001',delimiter=',',skiprows=0) #カンマ区切りの場合
data=np.loadtxt('./data/temp.j=middle.0000',skiprows=0)
data_t=np.transpose(data)
 
#リスト型に変換
x=list(data_t[0])
temp=list(data_t[1])

#graph(x,temp,"x","Temperature(K)","Temperature distribution")

#ここがメイン！！
#データを取得してアニメーション作成
fig = plt.figure()
ims=[]
for t in range(file_count):
    nstep100=files[t]
    
    #fileの取得
    data=np.loadtxt('./data/'+nstep100,skiprows=0)
    data_t=np.transpose(data)
    
    #リスト型に変換
    x=list(data_t[0])         
    temp=list(data_t[1])
    
    im = plt.plot(x,temp, "r")
    ims.append(im)


plt.grid()
plt.xlabel("x")
plt.ylabel("Temperature(K)")   
plt.xlim(0,200)
plt.ylim(0,2)
ims = animation.ArtistAnimation(fig, ims)