【第7回Python流体の数値計算】１次元拡散方程式を差分法で実装する。

今回は、「１次元の拡散方程式」をPythonで実装するというのをやります。

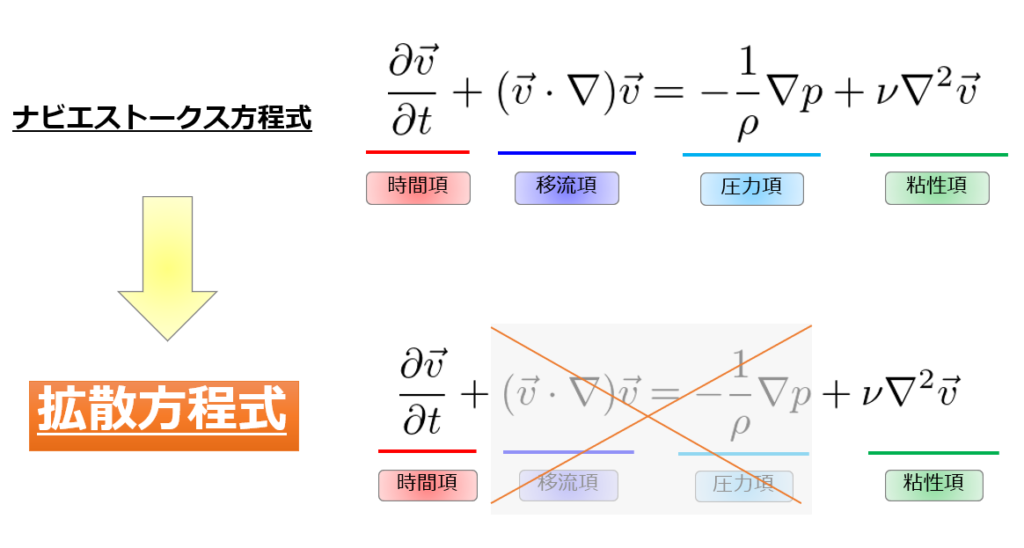
前回の記事では、クーラン条件より「１次元の移流方程式」についての数値的安定性の内容をまとめましたが、「１次元の拡散方程式」も数値的安定性の条件が存在します。
本記事では、わざと数値的に不安定な状態での数値計算もやりますので、解の振る舞いがどのようになるのかを確認しながら見ていただければと思います。

☟前回の記事がまだの人はこちらから

前回の記事はこちら

【第6回Python流体の数値計算】１次元移流方程式のクーラン条件を確認！数値的安定性（差分法）

本件の基本的な内容はこちらのサイトにそってやっていきます。

この記事ではこんな人を対象にしています。

こんな人が対象

Pythonを使い始めたけどどう使うかわからない
流体の数値計算をはじめて勉強する人

本記事シリーズの最終目標は、ナビエストークス方程式をPythonで実装することですが、いきなりナビエストークス方程式を実装するのは難しいので各項の意味を確認しながら進めていきたいと思います。

今回の内容はこちら

一次元拡散方程式の数値計算
拡散方程式の安定性

☟拡散方程式というのはナビエストークス方程式の「左辺の第一項と右辺第二項」のみを使った偏微分方程式です。

では、まずは「1次元拡散方程式とは何か」という話から始めたいと思います。

１次元の拡散方程式とは
拡散方程式を離散化する
フォン・ノイマンのフーリエ解析法
1. 時間が経つと波の振幅が大きくなる（大きくなると不安定）
「\(\alpha=\)0.1、0.5、1.0」と変えてシミュレーション
まとめ
Pythonの完全初心者は書籍で学ぶとよい
流体の勉強をしたい方
数値計算を勉強したい方

１次元の拡散方程式とは

拡散方程式について簡単に解説をしておこうと思います。

１次元の拡散方程式

\begin{align*}
\frac{\partial u}{\partial t}= \nu \frac{\partial^2 u}{\partial x^2} \tag{1}
\end{align*}

これは名前の通り、初期状態の形（速度、温度など）が系の中で均等になるように拡散する偏微分方程式です。

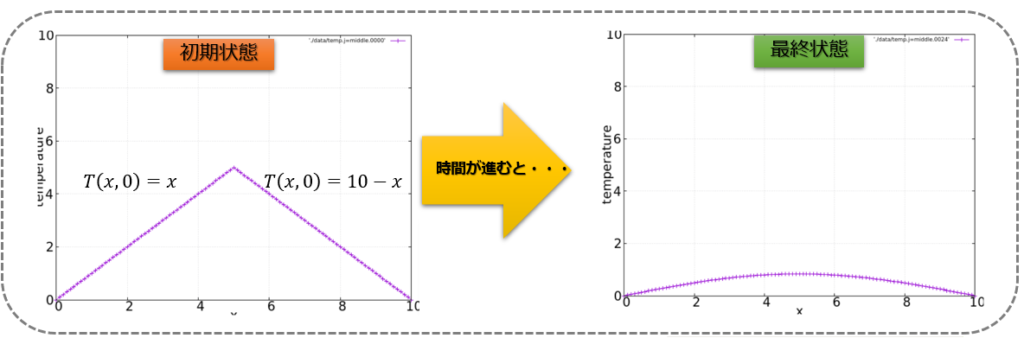
後ほど実際にPythonのコードを示しながらアニメーション作成を行いますので、その解の振る舞いを確認して理解を深めてもらえればと思います_(._.)_

拡散方程式を離散化する

拡散方程式を、

時間の一階微分の項
空間の二階微分の項

となっています。

時間の項に対しては、

時間微分の項（第一項）

\begin{align*}
\frac{\partial u}{\partial t} \approx \frac{u(t+\Delta t)-u(t)}{\Delta t}\tag{2}
\end{align*}

とします。

空間微分の項は、２次精度中心差分で行います。

ある位置\(x_0+\Delta x_0\)における\(x_0\)のまわりでテーラー展開を考えます。

\begin{align*}
u(x_0+\Delta x) = u(x_0) +\Delta x \frac{\partial u(x)}{\partial x}\bigg|_{x_0} + \frac{\Delta x^2}{2} \frac{\partial ^2 u(x)}{\partial x^2}\bigg|_{x_0} + \frac{\Delta x^3}{3!} \frac{\partial ^3 u(x)}{\partial x^3}\bigg|_{x_0} + O(\Delta x^4)\tag{3}
\end{align*}

さらに、

ある位置\(x_0-\Delta x_0\)における\(x_0\)のまわりでテーラー展開を考えます。

\begin{align*}
u(x_0-\Delta x) = u(x_0) -\Delta x \frac{\partial u(x)}{\partial x}\bigg|_{x_0} + \frac{\Delta x^2}{2} \frac{\partial ^2 u(x)}{\partial x^2}\bigg|_{x_0} – \frac{\Delta x^3}{3!} \frac{\partial ^3 u(x)}{\partial x^3}\bigg|_{x_0} + O(\Delta x^4)\tag{4}
\end{align*}

今ほしいのは、\(x_0\)における2階微分\(\frac{\partial ^2 u(x)}{\partial x^2}\bigg|_{x_0}\)なので(3)と(4)を足すことで、

\begin{align*}
\frac{\partial ^2 u}{\partial x^2}=\frac{u(x+\Delta x)-2u(x)+u(x-\Delta x)}{\Delta x^2} + O(\Delta x^2)
\end{align*}

得ることができます。

数値計算では離散化をしてある位置という任意の位置を指定することはできません。

つまり、空間は連続ではなく格子点でしか表現されていません。

ある位置\(x_0\)と書かずに、ある位置（格子点）\(i\)と書くのが一般的です。

そうすると上で行った計算は以下のように書くことができます。

\begin{align*}
u_{i+1} = u_i + \Delta x \frac{\partial u}{\partial x}\bigg|_i + \frac{\Delta x^2}{2} \frac{\partial ^2 u}{\partial x^2}\bigg|_i + \frac{\Delta x^3}{3!} \frac{\partial ^3 u}{\partial x^3}\bigg|_i + O(\Delta x^4)\tag{5}
\end{align*}

\begin{align*}
u_{i-1} = u_i – \Delta x \frac{\partial u}{\partial x}\bigg|_i + \frac{\Delta x^2}{2} \frac{\partial ^2 u}{\partial x^2}\bigg|_i – \frac{\Delta x^3}{3!} \frac{\partial ^3 u}{\partial x^3}\bigg|_i + O(\Delta x^4)\tag{6}
\end{align*}

(5)と(6)を足して、

\begin{align*}
u_{i+1} + u_{i-1} = 2u_i+\Delta x^2 \frac{\partial ^2 u}{\partial x^2}\bigg|_i + O(\Delta x^4)
\end{align*}

\(\frac{\partial ^2 u}{\partial x^2}\bigg|_i\)について少し整理をすると、

\begin{align*}\frac{\partial ^2 u}{\partial x^2}\bigg|_i=\frac{u_{i+1}-2u_{i}+u_{i-1}}{\Delta x^2} + O(\Delta x^2)\end{align*}

となります。

2次以降は無視をして計算をすることになるので、2次精度の微分ということになります。

以上より、(1)式の拡散方程式の離散化は以下のように書けることがわかりました。

\begin{align*}
\frac{u_{i}^{n+1}-u_{i}^{n}}{\Delta t}=\nu\frac{u_{i+1}^{n}-2u_{i}^{n}+u_{i-1}^{n}}{\Delta x^2}\tag{7}
\end{align*}

今、ほしい情報は「ある時刻置ける\(u(x)\)」です。

未来を知りたいのですから、今のステップ数を\(n\)とすると、ちょっと先の未来は\(n+1\)ステップです。

\begin{align*}
u_{i}^{n+1}=u_{i}^{n}+\frac{\nu\Delta t}{\Delta x^2}(u_{i+1}^{n}-2u_{i}^{n}+u_{i-1}^{n})\tag{8}
\end{align*}

では、さっそくPythonを使った拡散方程式の数値計算をと・・・・行きたいところですが、前回の記事で確認したような数値的な安定性条件を見ておきます。

フォン・ノイマンのフーリエ解析法

今回使う方法は、「フォン・ノイマンのフーリエ解析法」と呼ばれるものです。
名前だけで圧倒されそうな解法ですが、ポイントは以下となります。

【ポイント】

関数を波に分解→フーリエ変換（or フーリエ級数展開）
時間が経つと波の振幅が大きくなる（大きくなると不安定）

フーリエ変換について学びたい方は☟こちらからどうぞ！

「フーリエ変換」の記事はこちら

大学数学

では、本題に行きます(^^)/

時間が経つと波の振幅が大きくなる（大きくなると不安定）

(１)式を離散化して、時々刻々と変動する数値解を安定的求めるには、計算を進めるにあたって数値的な誤差が増大しないことが条件になります。
移流方程式には厳密解が存在するので、厳密解をとして\(\tilde{u}^{n}_{i}\)、数値解を\({u}^{n}_{i}\)とします。
そうすると、厳密解と数値解には誤差があるので誤差を\(\tilde{\epsilon}^{n}_{i}\)と置いておきしょう。

\begin{align*}
u^{n}_{i}=\tilde{u}^{n}_{i}+\tilde{\epsilon}^{n}_{i}
\end{align*}

これを(8)式に代入すると、誤差に関する方程式を得ることができます。

\begin{align*}
\tilde{\epsilon}^{n+1}_{i}=\tilde{\epsilon}^{n}_{i}+\frac{\nu\Delta t}{\Delta x^2}(\tilde{\epsilon}^{n}_{i+1}-2\tilde{\epsilon}^{n}_{i}+\tilde{\epsilon}^{n}_{i-1})\tag{8-1}
\end{align*}

誤差\(\tilde{\epsilon}^{n}_{i}\)、時刻\(n\)ステップと格子点\(i\)で以下のようにフーリエ級数展開を行います。

\begin{align*}
\tilde{\epsilon}^{n}_{i}=\sum A^{n}_{k}e^{Ik(i\Delta x)}\tag{9}
\end{align*}

これは、波数\(k\)の波\(e^{Ik(i\Delta x)}\)が\(A^{n}_{k}\)で重み付けされた形になっています。
※虚数は、格子点の\(i\)と紛らわしいので「虚数\(I\)」と表記しました。

これを(8-1)式に代入します。
(8-1)式は線形な方程式なので(9)式の和のほとんどは書かなくてもよくなります。

\begin{align*}
A^{n+1}_{k}=A^{n}_{k}+\alpha\bigg(A^{n}_{k}e^{Ik(i\Delta x)}-2A^{n}_{k}+A^{n}_{k}e^{-Ik(i\Delta x)}\bigg)\tag{10}
\end{align*}

※\(\alpha=\frac{\nu\Delta t}{\Delta x^2}\)と置いています。
これを今、以下のようにまとめます。

\begin{align*}
g& = \frac{A^{n+1}_{k}}{A^{n}_{k}}\\
& =1+\alpha\big(e^{Ik(i\Delta x)}-2+e^{-Ik(i\Delta x)}\big)\\
& =1-2\alpha\big(1-\cos\phi\big)
\end{align*}

※\(\phi=Ik\Delta x\)と置きました。
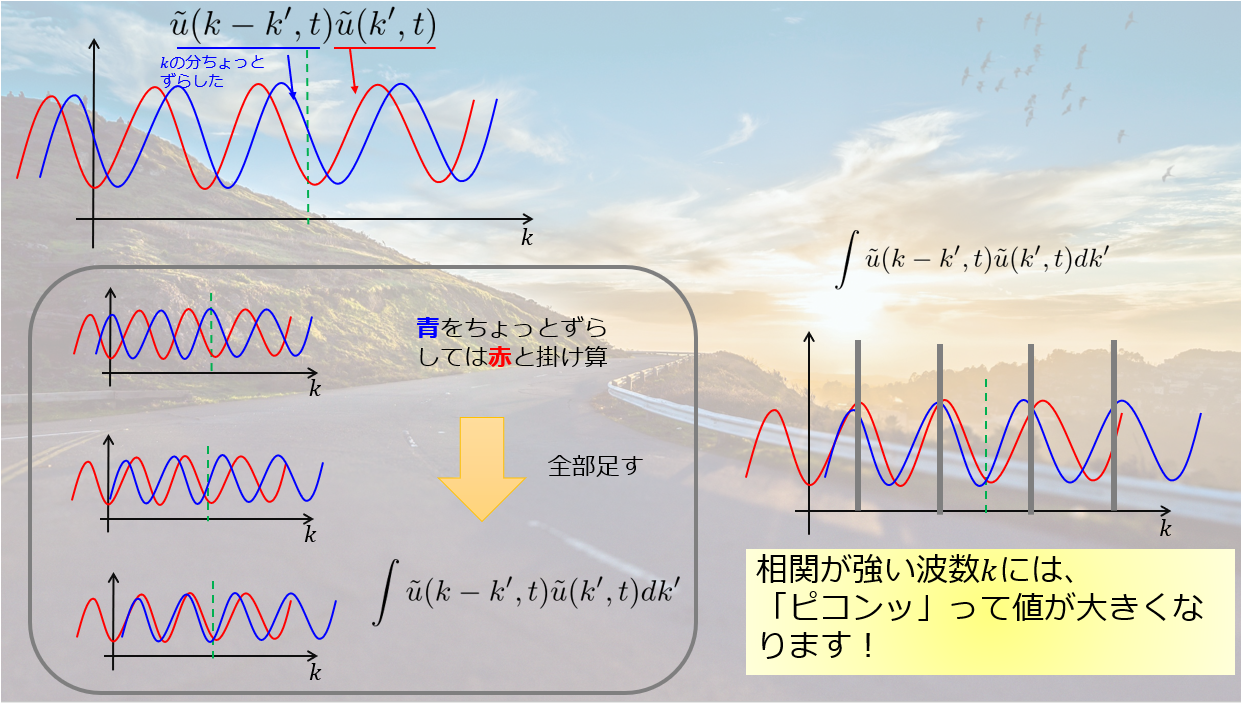
ちょっとわかりにくいので絵でイメージすると以下のようになります。

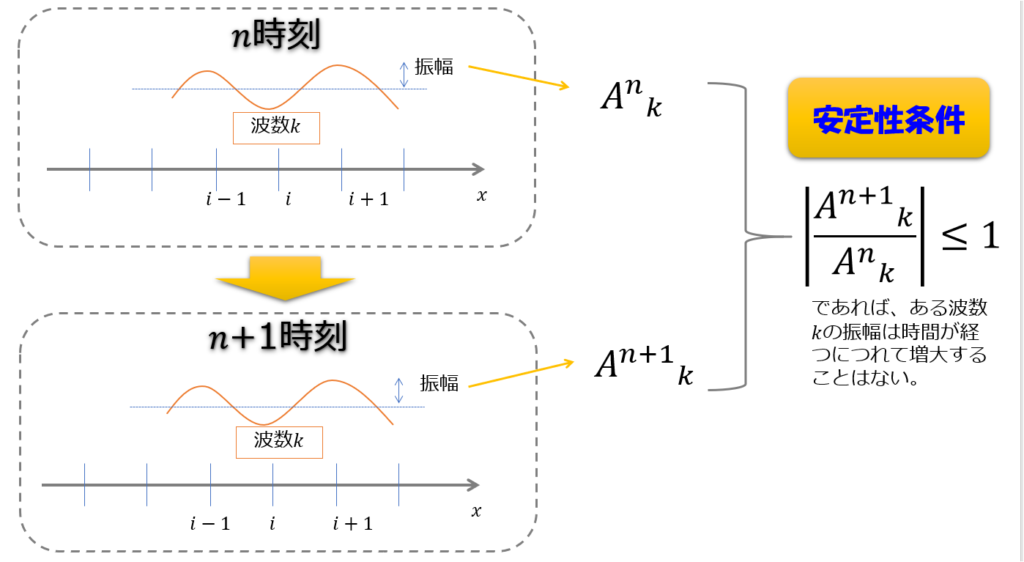
\(g = \frac{A^{n+1}_{k}}{A^{n}_{k}}\)が１より大きいという事は、ある波数\(k\)の重みがどんどん増大してやがて数値的には無視できないくらいの誤差になるということを意味しています。
つまり、「n+1ステップでの波数\(k\)の重み」と「nステップでの波数\(k\)の重み」\(g = \frac{A^{n+1}_{k}}{A^{n}_{k}}\)を考えたときに、

\begin{align*}
\left\{\begin{matrix}
|g|\leq 1\,\,\,\,(安定)\\
|g|> 1\,\,\,\,(不安定)
\end{matrix}\right.
\end{align*}

という判別ができます。
どんな\(\phi\)に対しても\(|g|\leq 1\)であれば安定解を得るということですね。
つまり・・・

\begin{align*}
-1\leq \alpha \leq 1
\end{align*}

すなわち、

\begin{align*}
-1\leq 1-2\alpha\big(1-\cos\phi\big)\leq 1\tag{11}
\end{align*}

となります。
今の場合、\(g\)はどんな\(\phi\)に対しても1より小さいので問題になってくるのは、\(-1\leq 1-2\alpha\bigg(1-\cos\phi\bigg)\)です。
一番厳しい条件は\(\cos\phi=-1\)なので、どんな\(\phi\)に対しても(11)が成立するためには、

\begin{align*}
\alpha\leq \frac{1}{2}\tag{12}
\end{align*}

となります。
ここで、数値計算においては\(\Delta x\)を決めた後に時間幅\(\Delta t\)をいくつにしようか考えることが多いので、\(\Delta t\)についての条件式に書き換えておきます。

\begin{align*}
\Delta t\leq \frac{\Delta x^2}{2\nu}\tag{13}
\end{align*}

このように、空間幅\(\Delta x\)に対して時間幅\(\Delta t\)は(13)式を満たしていなければ安定ではない解となってしまうということを意味しています。
では、いよいよPythonを使って「1次元の拡散方程式」を解いてみましょう。

(13)の条件を「満たすもの」と「満たさないもの」に分けててシミュレーションをしてみます。

カマキリ

ちなみに(13)の条件って名前があるんですかね？(/・ω・)/

「\(\alpha=\)0.1、0.5、1.0」と変えてシミュレーション

では、Google Colaboratoryを使ってコードを書いて、解の振る舞いをアニメーションで見て理解を深めていきたいと思います。

(13)式より、\(\alpha\)は0.5より小さくないと安定解を得ることができないとわかったので、色々値を変えて検証していきます。

【ポイント】
以下の３パターンで解析をします。

\(\alpha\)	解の振る舞い
0.1	？
0.5	？
1.0	？

基本となるPythonコードは以下となります。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import animation, rc
from IPython.display import HTML

nx = 41
dx = 2 / (nx-1)
nt = 25 
nu = 0.3 
alpha =1.0
dt = alpha* dx**2 /nu
print('dx=',dx)
print('dt=',dt)


x = np.linspace(0,2,nx)

un = []
u = np.ones(nx)
u[int(.5 / dx):int(1 / dx + 1)] = 2

fig = plt.figure(figsize=(8,4))
ims=[]
for n in range(nt): 
    un = u.copy()
    if (nt%1==0):
      im = plt.plot(x,u, "r")
      ims.append(im)
    for i in range(1, nx - 1):
      u[i] = un[i] + nu * dt / dx**2 * (un[i+1] - 2 * un[i] + un[i-1])
        
plt.grid()
plt.ylim([-0.1,3])
plt.xlabel("x")
plt.ylabel("u(m/s)")     
anim = animation.ArtistAnimation(fig, ims)
rc('animation', html='jshtml')
plt.close()
anim