こんにちは(@t_kun_kamakiri)(^^)/
前回では「逆行列の定義」と「その演習問題」についての内容をまとめました。
今回はクラメルの公式を使って連立方程式の解を求める方法を紹介します。
クラメルの公式を理解する。
これから線形代数を学ぶ学生や社会人のために「役に立つ内容にしたい」という思いで記事を書いていこうと考えています。
- 行列をはじめて習う高校生・大学生
- 仕事で行列を使うけど忘れてしまった社会人
この記事の内容をマスターして行列計算を楽に計算できるようになりましょう(^^)
クラメルの公式とは
クラメルの公式について後で詳しく解説するとして、ここではクラメルの公式のまとめを書き記すことにします。
未知数$x_{1},x_{2},\cdots ,x_{n}$の$n$個に対して連立方程式から解を求めることを考えます。
\left\{\begin{matrix}
a_{11}x_{1}+a_{12}x_{2}+\cdots +a_{1n}x_{n}=b_{1}\\
a_{21}x_{1}+a_{22}x_{2}+\cdots +a_{2n}x_{n}=b_{2}\\
\cdots\\
a_{n1}x_{1}+a_{n2}x_{2}+\cdots +a_{nn}x_{n}=b_{n}
\end{matrix}\right.
\end{align*}
これは$AX=b$のように行列でまとめることができ、$X$の$i$成分である$x_{i}$は以下で求まります。
x_{i}&=\frac{1}{|A|}\sum_{j=1}^{n}b_{j}\tilde{a}_{ji}\\
&=\frac{|A_{i}|}{|A|}
\end{align*}
※$|A_{i}|$は$i$列を$b$に置き換えた行列式
クラメルの公式の解説
クラメルの公式について解説を行います。
未知数$x_{1},x_{2},\cdots ,x_{n}$の$n$個に対して連立方程式から解を求めることを考えます。
\left\{\begin{matrix}
a_{11}x_{1}+a_{12}x_{2}+\cdots +a_{1n}x_{n}=b_{1}\\
a_{21}x_{1}+a_{22}x_{2}+\cdots +a_{2n}x_{n}=b_{2}\\
\cdots\\
a_{n1}x_{1}+a_{n2}x_{2}+\cdots +a_{nn}x_{n}=b_{n}
\end{matrix}\right.
\end{align*}
があるとします。
これを行列に書き換えることができ・・・
\begin{pmatrix}
a_{11} &a_{12} &\cdots &a_{1n} \\
a_{21} &a_{22} &\cdots &a_{2n} \\
\cdots & \cdots & \cdots &\cdots \\
a_{n1} &a_{n2} &\cdots &a_{nn}
\end{pmatrix}\begin{pmatrix}
x_{1}\\
x_{2}\\
\cdots\\
x_{n}
\end{pmatrix}=
\begin{pmatrix}
b_{1}\\
b_{2}\\
\cdots\\
b_{n}
\end{pmatrix}
\end{align*}
となります。
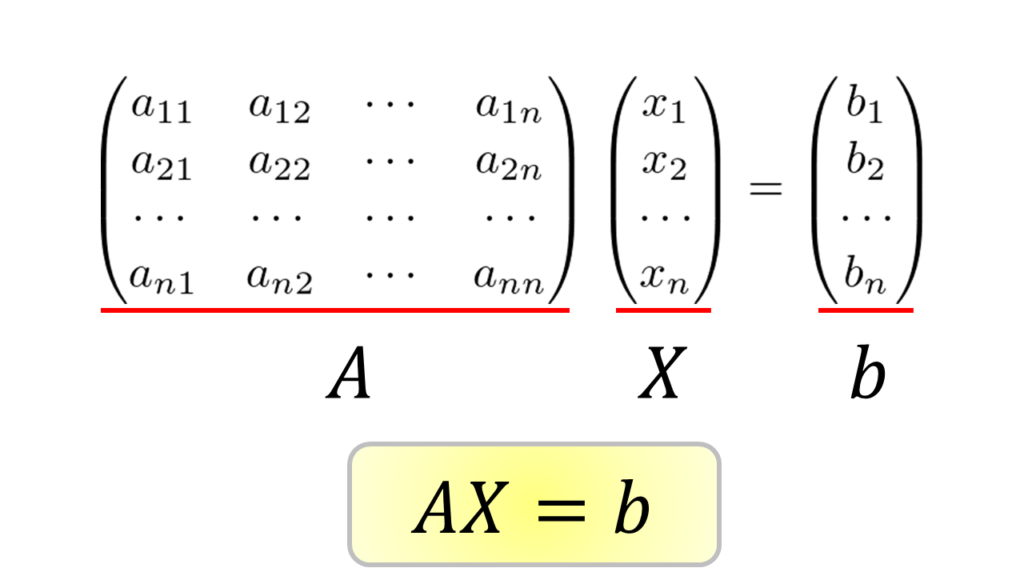

目的は$X=\begin{pmatrix}
x_{1}\\
x_{2}\\
\cdots\\
x_{n}
\end{pmatrix}$を知ることです。
ここで行列$A$に逆行列$A^{-1}$が存在すれば、$AX=B$の左から$A^{-1}$を作用させて、
\underset{単位行列E}{A^{-1}A}X &=A^{-1}b\\
EX&=A^{-1}b
\end{align*}
となり、$X=A^{-1}b$により簡単に$X$が求まります。
前回の記事で$A^{-1}=\frac{1}{|A|}\tilde{A}$($\tilde{A}$ は余因子行列)という解説をしましたので、$X=A^{-1}b$の行列計算を進めることにします。
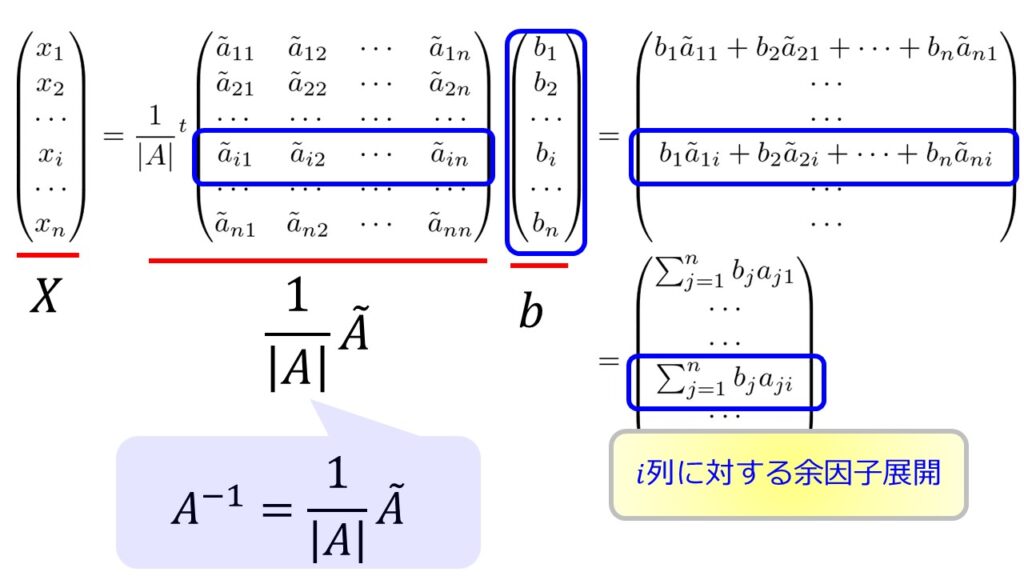

$x_{i}$だけを抜き取って書くと、
x_{i}&=\frac{1}{|A|}\sum_{j=1}^{n}b_{j}\tilde{a}_{ji}\\
&=\frac{|A_{i}|}{|A|}
\end{align*}
となっています。
※$|A_{i}|$は$i$列を$b$に置き換えた行列式
$\sum_{j=1}^{n}b_{j}\tilde{a}_{ji}$が、$i$列をbに置き換えた余因子展開であることに気付けば$|A|$に対して$i$列をbに置き換えた行列式が、$\sum_{j=1}^{n}b_{j}\tilde{a}_{ji}$であることがわかるでしょう。
クラメルの公式のまとめ
クラメルの公式の一般的な内容をまとめました。
未知数$x_{1},x_{2},\cdots ,x_{n}$の$n$個に対して連立方程式から解を求めることを考えます。
\left\{\begin{matrix}
a_{11}x_{1}+a_{12}x_{2}+\cdots +a_{1n}x_{n}=b_{1}\\
a_{21}x_{1}+a_{22}x_{2}+\cdots +a_{2n}x_{n}=b_{2}\\
\cdots\\
a_{n1}x_{1}+a_{n2}x_{2}+\cdots +a_{nn}x_{n}=b_{n}
\end{matrix}\right.
\end{align*}
これは$AX=b$のように行列でまとめることができ、$X$の$i$成分である$x_{i}$は以下で求まります。
x_{i}&=\frac{1}{|A|}\sum_{j=1}^{n}b_{j}\tilde{a}_{ji}\\
&=\frac{|A_{i}|}{|A|}
\end{align*}
※$|A_{i}|$は$i$列を$b$に置き換えた行列式
次回はこちらの3つの方程式の解$(x,y,z)$をクラメルの公式を用いて求めます。
x+y+z&=1\\
ax+by+cz&=d\\
a^2 x+b^2 y +c^2 z&=d^2
\end{align*}
参考にする参考書はこれ
当ブログでは、以下の2つの参考書を読みながらよく使う内容をかいつまんで、一通り勉強すればついていけるような内容を目指していこうと思います。
大事なところをかいつまんで、「これはよく使うよな。これを理解するためには補足で説明をする」という調子で進めていきます(^^)/