どうも(^^)/
あまり使う機会がないですがPythonを用いて、円周率を計算したいと思います。
本日の内容
モンテカルロ法を用いて円周率をPythonで計算してみる
お遊びですので、Pythonコードもちょちょいって感じで作ってみました。
内容はこちらの本に書いてあったので紹介したいと思います。
モンテカルロ法とは
モンテカルロ法 とはシミュレーションや数値計算を乱数を用いて行う手法の総称のことです。
（例が思いついたら追記します）
モンテカルロ法を用いて円周率を近似してみよう
数値計算での考え方は、まず一辺が長さ\(a\)の正方形を用意します。
そこに、
- 0～1の値をランダムにm個の点を打っていきます。
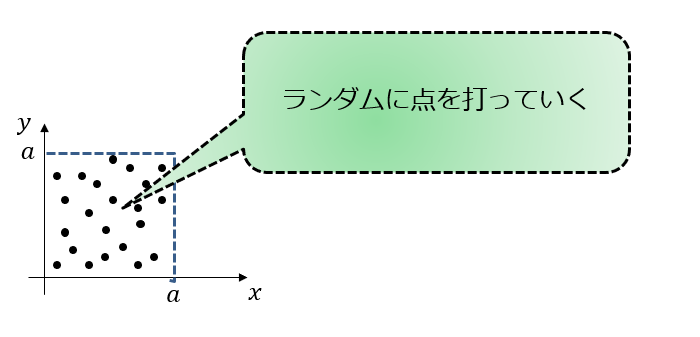
そうすると、数密度が
\begin{align*}
\rho_{a}=\frac{m}{a^{2}}\tag{1}
\end{align*}
\rho_{a}=\frac{m}{a^{2}}\tag{1}
\end{align*}
となります。
次に、
- 半径\(a\)の1/4円を用意して、先ほどの点の内、1/4円に入った数をカウントします。
1/4円に入った数が\(n\)個なら、数密度は
\begin{align*}
\rho_{c}=\frac{n}{\pi a^{2}/4}\tag{2}
\end{align*}
\rho_{c}=\frac{n}{\pi a^{2}/4}\tag{2}
\end{align*}
となります。
乱数を用いているので、点を一様に配置してくれるとすると数密度は両者で同じです。
\begin{align*}
\rho_{a}=\rho_{c}\tag{3}
\end{align*}
\rho_{a}=\rho_{c}\tag{3}
\end{align*}
なので、(1)(2)式より、
\begin{align*}
\pi=4\frac{n}{m}\tag{4}
\end{align*}
\pi=4\frac{n}{m}\tag{4}
\end{align*}
と、円周率が近似的に求まることがわかりました。
以上の流れをまとめると・・・
乱数で点を打ちつけていく数が多ければ多いほど、円周率に近づきそうです。
円周率をPythonを用いて近似してみる
では、先ほど説明した内容でアルゴリズムを書いていきましょう。
乱数の数は最大で\(m=1000\)にしておきます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
import numpy as np import matplotlib.pyplot as plt import random m=0 num=[] pi=[] pi_a=[] for m in range(1,1000): n=0 for i in range(m): x=random.uniform(0,1) y=random.uniform(0,1) if (x**2+y**2<=1.0): n=n+1 pi.append(4.0*n/m) num.append(m) pi_a.append(np.pi) #グラフの作成 plt.plot(num,pi,label="4*n/m") plt.plot(num,pi_a,label="pi") ##フォントサイズの指定 plt.xticks(fontsize=7) plt.yticks(fontsize=7) ##グリッドの有無 plt.grid(True) ##x軸とy軸のラベル plt.xlabel("number") plt.ylabel("pi") ##x軸とy軸のラベル plt.legend(loc="upper right") ##グラフを描く plt.show() |
結果
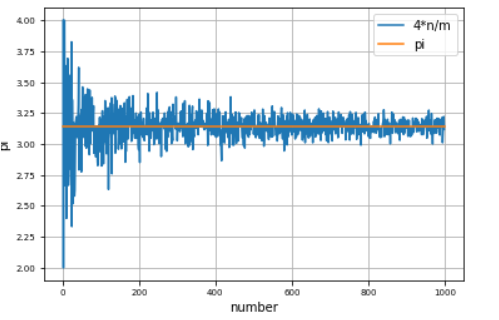
- 横軸：乱数（点を打った数）
- 縦軸：円周率の近似式\(4\frac{n}{m}\)
オレンジの実線が真の円周率の値です。
最大で乱数の数を1000個にまで計算させました。
乱数の数が多いと、真の円周率の値に近づいていっているのがわかります。
Follow @t_kun_kamakiri
