こんにちは(@t_kun_kamakiri)(^^)/
この記事ではフーリエ変換について説明したいと思います!
フーリエ変換にまつわる理論面でのお話は知らないといけないことをがとても多いです。
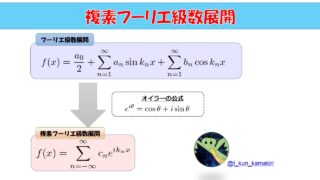
複素フーリエ級数展開
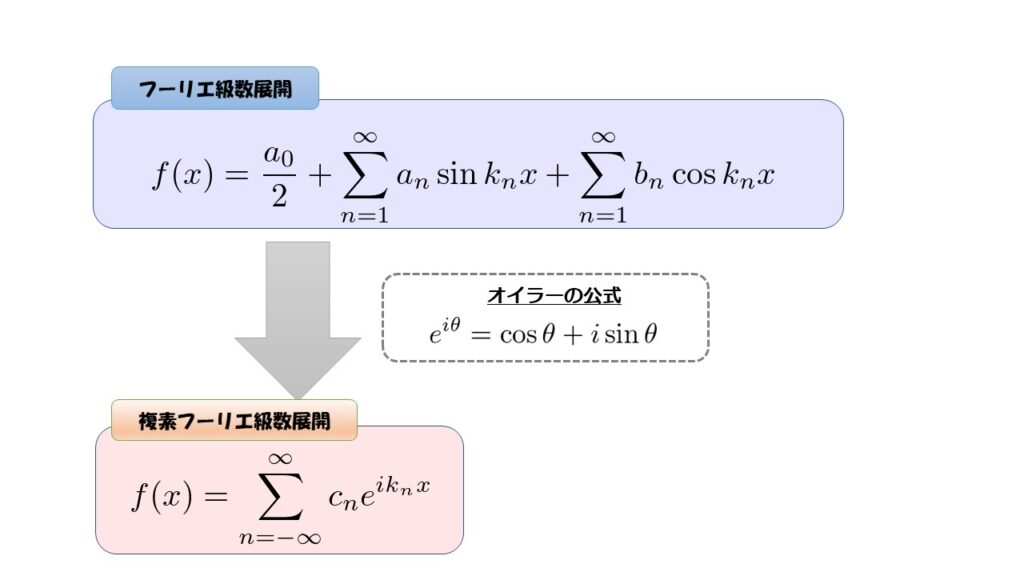
※\(k_{n}=\frac{n\pi}{L}\)
として、任意関数\(f(x)\)は
と書けるよ、という話をしたいと思います。
これは複素フーリエ級数展開と呼ばれています。
係数\(c_{n}\)は、
c_{n}=\frac{1}{2L}\int^{L}_{-L}f(x)e^{-ik_{n}x}\ dx\tag{2}
\end{align*}
※\(e^{ik_{n}x}\)は\(2L\)周期関数ですので、任意関数\(f(x)\)も同じ\(2L\)周期関数に限った話であることに注意しましょう。
複素フーリエ級数展開では、正弦波\(e^{ik_n x}\)(\(k_n=\frac{n\pi}{L}\))が\(2L\)の周期性を持っているため、それらの正弦波で級数展開で記述できる\(f(x)\)も\(2L\)の周期性を持っているのでした。
しかし、\(L\rightarrow \infty\)とすると周期性は無くなり、非周期関数\(f(x)\)も正弦波\(e^{ik x}\)で記述できるフーリエ変換というのが本記事の内容です。
複素フーリエ級数展開の復習
まずはじめに複素フーリエ級数展開の復習をしておきましょう。
複素フーリエ級数展開を得る流れは以下の通りです。



- 任意の\(2L\)の周期関数\(f(x)\)をフーリエ級数展開する
- オイラーの公式を使って複素数まで考え方を広げる
- 複素フーリエ級数展開を得る
複素フーリエ級数展開
係数\(c_{n}\)は、
c_{n}=\frac{1}{2L}\int^{L}_{-L}f(x)e^{ik_{n}x}\ dx\tag{2}
\end{align*}
- 離散的な正弦波\(e^{ik_n x}\)で級数展開をしている
- \(2L\)の周期性のある関数\(f(x)\)を表現している
それと比べてフーリエ変換でのポイントさえ押させておけば、複素フーリエ級数展開からフーリエ変換に移行することができます。
- 任意の関数\(f(x)\)連続的な正弦波\(e^{ikx}\)の重ね合わせ
- 非周期関数\(f(x)\)をフーリエ変換で表現している(\(f(x)\)に周期性が無くても良い)
以上のポイントを踏まえてフーリエ変換を示していきましょう。
複素フーリエ級数展開:正規直交関数系で級数展開
関数の集合を、
としていると、直交性として、
\int _{-L}^{L}e^{ik_{m}x}e^{-ik_{n}x}\ dx=\left\{\begin{matrix}
2L\left ( m=n \right )\\0\left (m \neq n \right )
\end{matrix}\right.
\end{align*}
が得られますが・・・・・関数の集合を、
\int _{-L}^{L}\frac{1}{\sqrt{2L}}e^{ik_{m}x}\frac{1}{\sqrt{2L}}e^{-ik_{n}x}\ dx=\left\{\begin{matrix}1
\left ( m=n \right )\\0\left (m \neq n \right )
\end{matrix}\right.\tag{3}
\end{align*}
としておくと、関数の集合が
- 同じ関数\(m=n\)の複素共役同士の掛け算の積分は1であり、
- 異なる関数\(m\neq n\)の複素共役同士の掛け算の積分は値が0になる
を満たします。
これらの関数の集合を正規直交関数系と呼びます。
そうすると、\(2L\)の任意の周期関数\(f(x)\)を複素フーリエ級数展開すると、
係数\(c_{n}\)は、
c_{n}=\frac{1}{\sqrt{2L}}\int^{L}_{-L}f(x)e^{-ik_{n}x}\ dx\tag{5}
\end{align*}
となります。
(1)(2)式と(4)(5)式を比べると係数の違うくらいで本質的な部分(\(f(x)\)が周期の異なる関数\(e^{ik_n x}\)で展開されている)は変わっていません。
フーリエ変換:\(L\rightarrow \infty\)とする
と置きます。そうすると、
f(x)=\frac{1}{\sqrt{2L}}\sum_{n=-\infty}^{\infty}c_{n}e^{ik_{n}x}\\
c_{n}=\frac{1}{\sqrt{2L}}\int^{L}_{-L}f(x)e^{-ik_{n}x}\ dx
\end{align*}
↓\(F_{n}=\frac{L}{\pi}c_{n}\)
f(x)=\frac{1}{\sqrt{2\pi}}\sum_{n=-\infty}^{\infty}F_{n}e^{ik_{n}x}\frac{\pi}{L}\\
F_{n}=\frac{1}{\sqrt{2\pi}}\int^{L}_{-L}f(x)e^{-ik_{n}x}\ dx\tag{6}
\end{align*}
ここで、\(k_{n}=\frac{n\pi}{L}\)であるから、\(\frac{\pi}{L}\)が図のように関数をブロックで分割したときの幅となります。
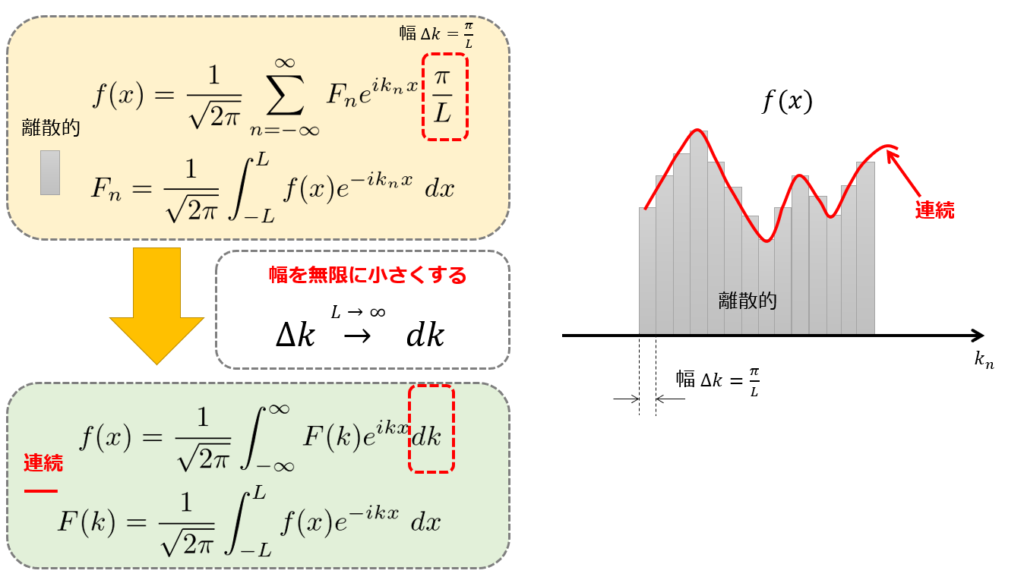

絵のように、\(f(x)\)は離散的で幅が\(\frac{\pi}{L}\)のブロックを足していく(灰色)ということは、幅を無限に小さくした際には積分(赤線)を計算しているということを意味しています。
このとき、とびとびの値だった\(\frac{n\pi}{L}\)が連続的な値\(k\)に変わります。
というわけで、\(L\rightarrow \infty\)とすることで、
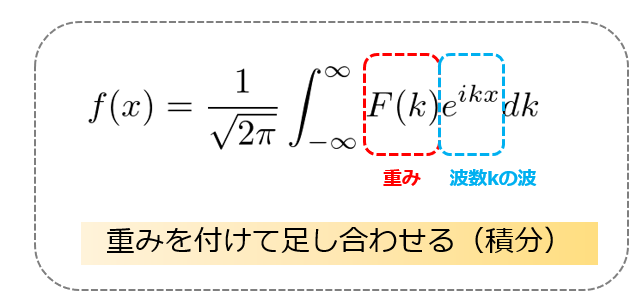
f(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}F(k)e^{ikx}dk\\
F(k)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}f(x)e^{ikx}\ dx\tag{7}
\end{align*}
これらの変換のことを「フーリエ変換」と「逆フーリエ変換」と呼びます。 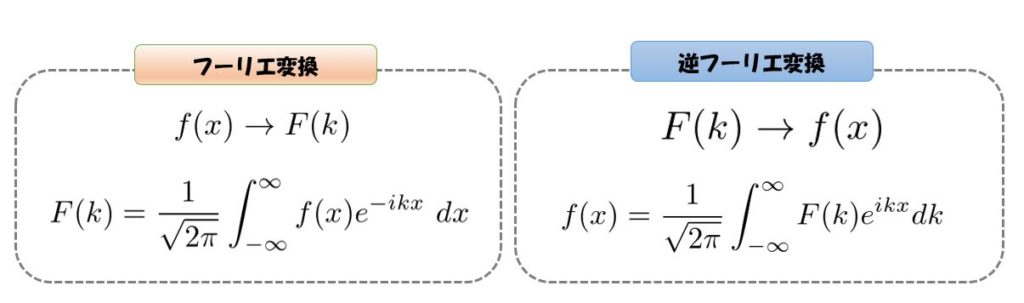
フーリエ変換の意味
「フーリエ変換」と「逆フーリエ変換」とはどういう変換の事なのかというのは(7)式を見れば表式はわかると思います・・・・が、
その変換の意味するところは何かということまで理解して覚えておきましょう(^^)/
フーリエ変換ではなくフーリエ級数展開で考えることにします。
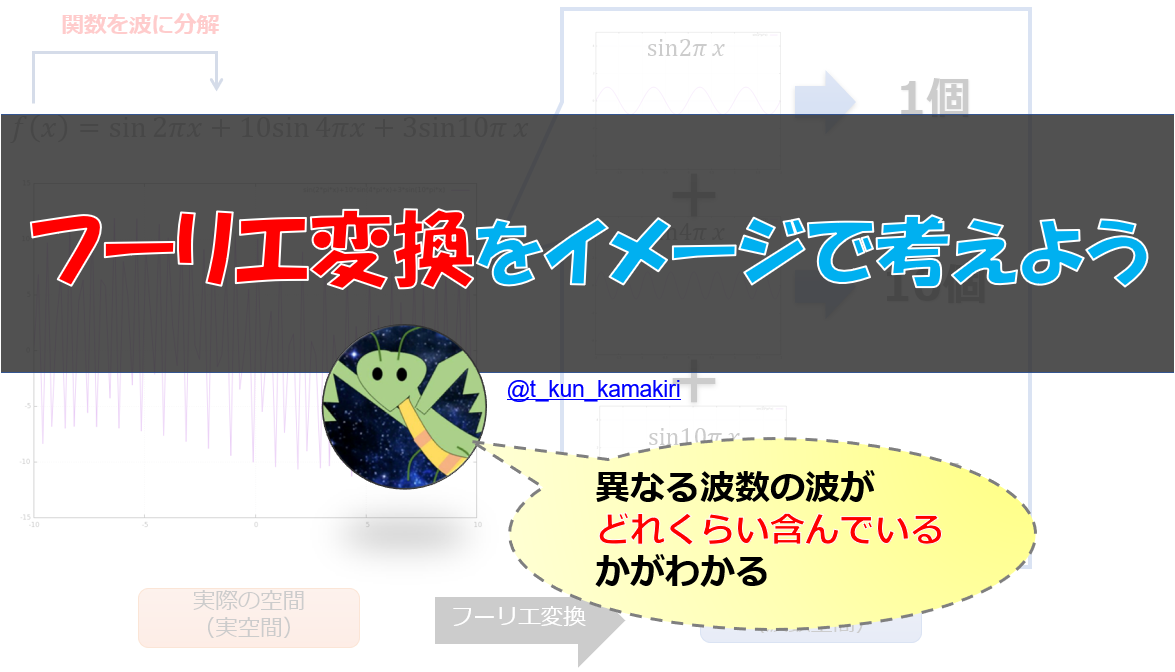
フーリエ級数展開は下記のようにある関数\(f(x)\)を、\(\sin\)波や\(\cos\)波や正弦波\(e^{ikx}\)などの様々な異なる波数の波に分解して波の空間(波数空間)に変換する方法のことです。
どんな関数も異なる波数の\(sin\)波の和で書いてやるのです。↓こんな感じです。
※以下の場合は周期関数\(f(x)\)に関して、例を挙げています。


こうやって考えると、「おや?\(\sin2\pi x\)(周期1)の波が1個か・・・・\(\sin10\pi x\)(周期1/10)の波が10個か・・・」と、波のくせに数えれるという恩恵を受けることができます。
- 「1個、10個、3個」とか書いたものがフーリエ変換(or フーリエ級数展開)した後の関数(波数空間での関数)のこと
- 「1個、10個、3個」は各波数の波の振幅
と考えることができます。
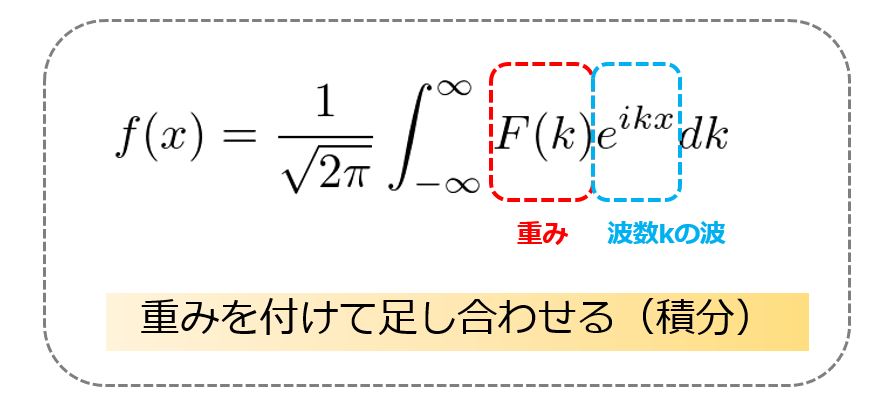
フーリエ変換も同じ考え方をして、ある波数\(k\)の波に対して重み(どれだけの強さを持っているか)を掛けて、全ての波数\(k\)で積分する。
という意味があるというのがわかります。

まとめ
今までのところをまとめておきましょう(^^)/



フーリエ変換のポイント
- 任意の関数\(f(x)\)連続的な正弦波\(e^{ikx}\)の重ね合わせ
- 非周期関数\(f(x)\)をフーリエ変換で表現している(\(f(x)\)に周期性が無くても良い)
フーリエ変換は、ある波数\(k\)の波に対して重み(どれだけの強さを持っているか)を掛けて、全ての波数\(k\)で積分する。
という意味があるというのがわかります。