大学数学

【複素フーリエ級数展開】オイラーの公式を使ってフーリエ級数展開式を使って書き変えよう。

こんにちは(@t_kun_kamakiri)(^^)/

この記事では複素フーリエ級数展開について説明したいと思います！

前回の記事で以下のようことを書きました。

前回の記事

直交関数系をベクトルの線形結合と類似して考えてみよう。

関数の直交性

今、\(x\)の範囲を[\(-L\leq x\leq L\)]とします。※\(x\)の範囲は考えやすくするために[\(-L\leq x\leq L\)]とします。
関数の集合\(\left \{f_{0}(x), f_{1}(x)\cdot\cdot\cdot,f_{n}(x)\right \}\)を用意し、
これらの関数の集合を使って、

\begin{align*}
\int _{-L}^{L}f_{i}(x)f_{j}(x)\ dx=\left\{\begin{matrix}
1\left ( i=j \right )\\0\left ( i\neq j \right )
\end{matrix}\right.
\end{align*}

を満たすことを関数の直交性といいます。
これらの関数の集合を直交関数系といいます。
これらの関数の集合\(\left \{f_{0}(x), f_{1}(x),\cdots,f_{n}(x)\right \}\)を用いて任意の関数\(f(x)\)は、
\begin{align*}f(x)=a_{0}f_{0}(x)+a_{1}f_{1}(x)+a_{2}f_{2}(x)+\cdots+a_{n}f_{n}(x)=\sum^{n}_{i=0}a_{i}f_{i}(x)\end{align*}

では、関数の集合を(1)のように直交性を満たす三角関数(sin、cos)として考えます。

フーリエ級数展開

\(x\)の範囲を[\(-L\leq x\leq L\)]とし、関数の集合を、

\begin{align*}\{1,\sin k_{1}x,\sin k_{2}x,\cdots,\sin k_{n}x,\cdots,\cos k_{1}x,\cos k_{2}x,\cdots,\cos k_{n}x,\cdots \}\end{align*}

※\(k_{n}=\frac{n\pi}{L}\)
として、任意関数\(f(x)\)は
\begin{align*}f(x)  = \frac{a_{0}}{2}+\sum^{\infty}_{n=1}a_{n}\sin k_{n}x+\sum^{\infty}_{n=1}b_{n}\cos k_{n}x\end{align*}

と書けます。
これはフーリエ級数展開と呼ばれています。
関数の集合は、
\begin{align*}
\left\{\begin{matrix}
\int_{-L}^{L}\sin k_{i}x\sin k_{j}x \ dx=L\delta_{ij}\\
\\
\int_{-L}^{L}\cos k_{i}x\cos k_{j}x \ dx =L\delta_{ij}\\
\\
\int_{-L}^{L}\sin k_{i}x\cos k_{j}x \ dx=L\delta_{ij}
\end{matrix}\right.
\end{align*}

の直交性を満たします。
※\(\sin,\cos\)が\(2L\)の周期関数であるので、\(f(x)\)も\(2L\)の周期関数
フーリエ級数展開の係数\(a_{n},b_{n}\)
\begin{align*}
a_{n}=\frac{1}{L}\int^{L}_{-L}f(x)\sin k_{n}x\ dx
\end{align*}

\begin{align*}
b_{n}=\frac{1}{L}\int^{L}_{-L}f(x)\cos k_{n}x\ dx
\end{align*}

前回の記事

【フーリエ級数展開】直交関数系を使って任意関数を表そう。

カマキリ

ここまでが前回までの内容

本記事では、

本記事の内容

複素フーリエ級数展開

\(x\)の範囲を[\(-L\leq x\leq L\)]とし、関数の集合を、

\begin{align*}\{1,e^{ik_{1}x},e^{ik_{2}x},\cdots,e^{ik_{n}x},\cdots,e^{-ik_{1}x},e^{-ik_{2}x},\cdots,e^{-ik_{n}x},\cdots\}\end{align*}

※\(k_{n}=\frac{n\pi}{L}\)
として、任意関数\(f(x)\)は
\begin{align*}f(x)  = \sum_{n=-\infty}^{\infty}c_{n}e^{ik_{n}x}\end{align*}

と書けるよ、という話をしたいと思います。
これは複素フーリエ級数展開と呼ばれています。
係数\(c_{n}\)は、
\begin{align*}
c_{n}=\frac{1}{2L}\int^{L}_{-L}f(x)e^{-ik_{n}x}\ dx\tag{12}
\end{align*}

※\(e^{ik_{n}x}\)は\(2L\)周期関数ですので、任意関数\(f(x)\)も同じ\(2L\)周期関数に限った話であることに注意しましょう。

道具としてのフーリエ解析

道具としてのフーリエ解析

涌井 良幸, 涌井 貞美
2,560円(11/21 17:49時点)

Amazon楽天市場Yahoo

Amazonの情報を掲載しています
物理現象のフーリエ解析 (ちくま学芸文庫)

物理現象のフーリエ解析 (ちくま学芸文庫)

小出 昭一郎
1,430円(11/21 08:18時点)

Amazon楽天市場Yahoo

Amazonの情報を掲載しています
スポンサーリンク

目次
  1. オイラーの公式を使ってフーリエ級数展開のサイン、コサインを指数関数で書いてみよう
  2. 関数の直交性を確認しよう
  3. 複素フーリエ級数展開の係数\(c_{n}\)はどのように記述できるのか
  4. まとめ

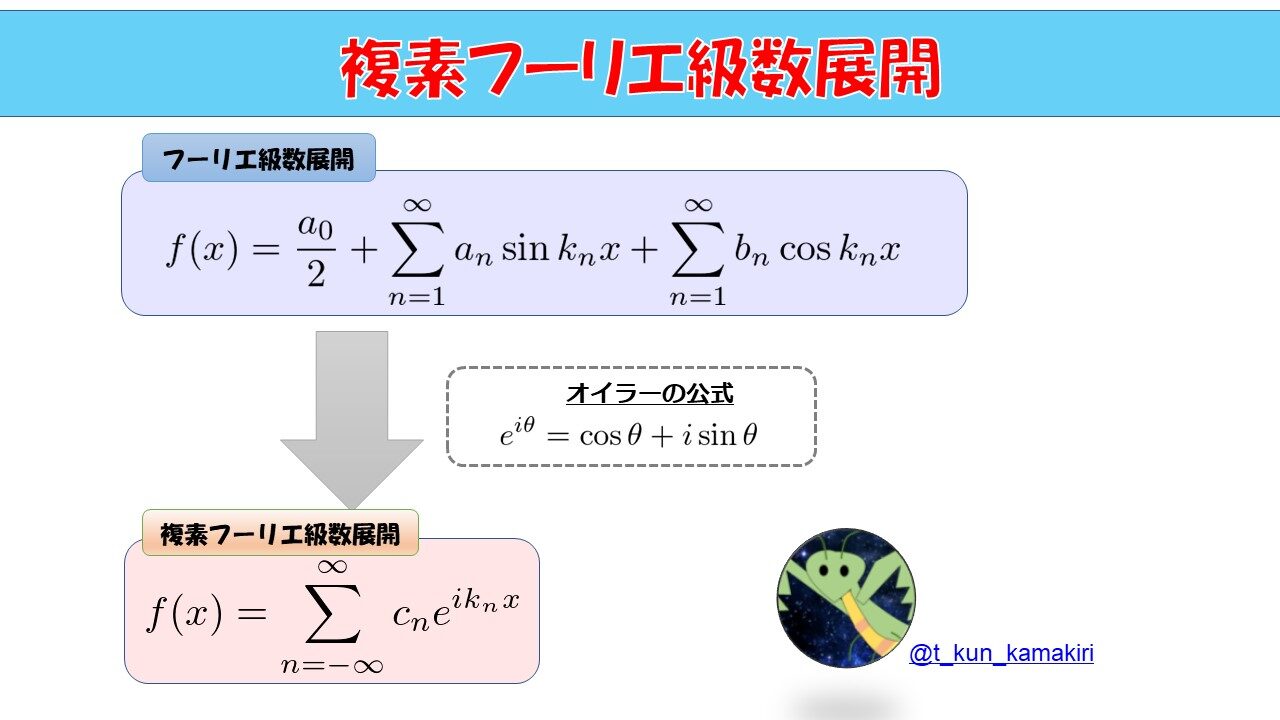
オイラーの公式を使ってフーリエ級数展開のサイン、コサインを指数関数で書いてみよう

今から行う流れを示しておきましょう。

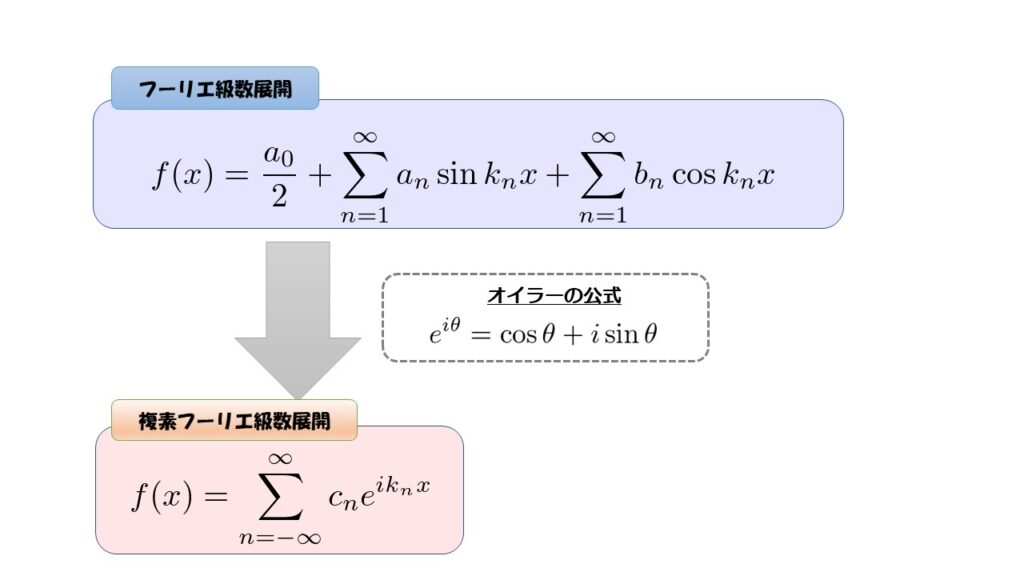
フーリエ級数展開から、複素フーリエ級数展開を考えていきます。

\(x\)の範囲を[\(-L\leq x\leq L\)]とし、関数の集合を、

\begin{align*}\{1,\sin k_{1}x,\sin k_{2}x,\cdots,\sin k_{n}x,\cdots,\cos k_{1}x,\cos k_{2}x,\cdots,\cos k_{n}x,\cdots \}\end{align*}

※\(k_{n}=\frac{n\pi}{L}\)

として、任意関数\(f(x)\)は

\begin{align*}f(x)  = \frac{a_{0}}{2}+\sum^{\infty}_{n=1}a_{n}\sin k_{n}x+\sum^{\infty}_{n=1}b_{n}\cos k_{n}x\tag{1}\end{align*}

と記述できるというのがフーリエ級数展開というのを前段でお話しました。

しかし、\(\sin\)、\(\cos\)の三角関数ではちょっと扱いにくいことが多いですし、

級数展開が\(\sin\)と\(\cos\)で別れているのもちょっと見にくいです。

フーリエ級数展開を複素数まで視野を広げて、指数関数\(e\)を使って見やすくしてやりましょう！

それにはオイラーの公式を使います。

オイラーの公式

\begin{align*}
e^{i\theta}=\cos\theta +i\sin\theta\tag{2}
\end{align*}

このようなオイラーの公式と呼ばれている「指数関数と虚数\(i\)と三角関数」が結びついているような奇跡の公式があります。

これを使いましょう！

\(-\theta\)のオイラーの公式も用意しておいて・・・

\begin{align*}
\left\{\begin{matrix}
e^{i\theta}=\cos\theta +i\sin\theta\\
e^{-i\theta}=\cos\theta -i\sin\theta
\end{matrix}\right.\tag{3}
\end{align*}

(3)式を使って、

\begin{align*}
\left\{\begin{matrix}
\cos\theta=\frac{e^{i\theta}+e^{-i\theta}}{2}\\
\sin\theta=\frac{e^{i\theta}-e^{-i\theta}}{2i}
\end{matrix}\right.\tag{4}
\end{align*}

(4)式を(1)式の\(\sin,\cos\)に代入します。

\begin{align*}
f(x)  &= \frac{a_{0}}{2}+\sum^{\infty}_{n=1}a_{n}\frac{e^{ik_{n}x}-e^{-ik_{n}x}}{2i}+\sum^{\infty}_{n=1}b_{n}\frac{e^{ik_{n}x}+e^{-ik_{n}x}}{2}\\
& = \frac{a_{0}}{2}+\sum^{\infty}_{n=1}\bigg[\frac{1}{2}\big(a_{n}-ib_{n}\big)e^{ik_{n}x}+\frac{1}{2}\big(a_{n}+ib_{n}\big)e^{-ik_{n}x}\bigg]\tag{5}
\end{align*}

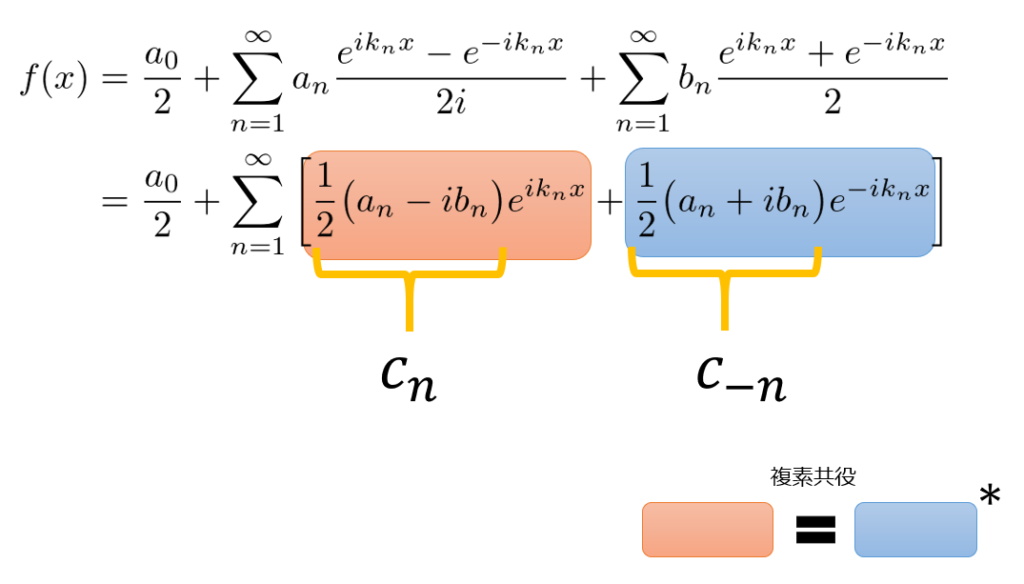
指数関数の係数を\(c_{n}\)と\(c_{-n}(=c^{*})\)とおいてやります。

そうすると、

\begin{align*}
f(x)=\frac{a_{0}}{2}+\sum^{\infty}_{n=1}\bigg(c_{n}e^{ik_{n}x}+c_{-n}e^{-ik_{n}x}\big)\tag{6}
\end{align*}

とまとめることができました。

ここからもう少しまとめることができます。

\(k_{n}=\frac{n\pi}{L}\)とおいていたので、(6)式を展開します。

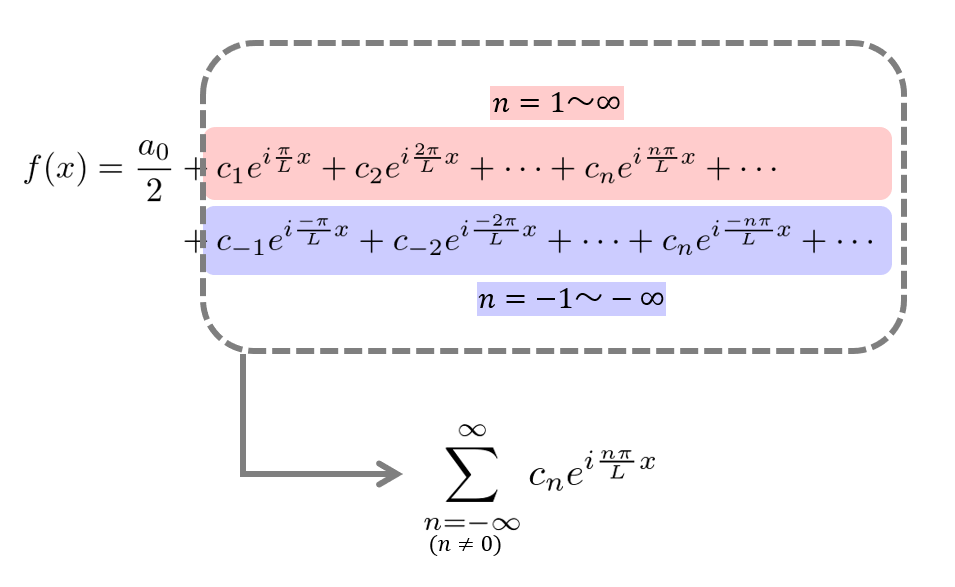
和の部分をまとめることができました。

ただ、フーリエ級数展開の(1)式のときは、和の\(n=0\)も含めてしまうと\(\sin,\cos\)の両方に\(n=\)の係数が出てきてしまうので和には\(n=0\)を含めませんでしたが、今回は\(n=0\)も和に含めてしまった方がすっきりするので、

\begin{align*}
c_{0}=\frac{a_{0}}{2}
\end{align*}

と書いておくと、

\begin{align*}
f(x)=\sum^{\infty}_{n=-\infty}c_{n}e^{ik_{n}x}\tag{7}
\end{align*}

と書くことができます。

これを複素フーリエ級数展開といいます。

カマキリ

式の形がずいぶんスッキリ！

関数の直交性を確認しよう

\(x\)の範囲を[\(-L\leq x\leq L\)]とし、関数の集合、

\begin{align*}\{1,e^{ik_{1}x},e^{ik_{2}x},\cdots,e^{ik_{n}x},\cdots,e^{-ik_{1}x},e^{-ik_{2}x},\cdots,e^{-ik_{n}x},\cdots\}\end{align*}

※\(k_{n}=\frac{n\pi}{L}\)

が関数の直交性を満たしているかを確認しておきましょう。

関数の直交性とは、関数の集合\(\left \{f_{0}(x), f_{1}(x)\cdot\cdot\cdot,f_{n}(x)\right \}\)を用意し、
これらの関数の集合を使って、

\begin{align*}
\int _{-L}^{L}f_{i}(x)f_{j}(x)\ dx=\left\{\begin{matrix}
1\left ( i=j \right )\\0\left ( i\neq j \right )
\end{matrix}\right.
\end{align*}

と表せることでしたが、複素関数の場合は異なる関数（もしくは自身と同じ関数）との複素共役との掛け算を積分した値が以下を満たすときに関数の直交性があると呼びます。

\begin{align*}
\int _{-L}^{L}f_{i}(x)f_{j}^{*}(x)\ dx=\left\{\begin{matrix}
1\left ( i=j \right )\\0\left ( i\neq j \right )
\end{matrix}\right.
\end{align*}

つまり、今の場合は↓これです。

\begin{align*}
\int _{-L}^{L}e^{ik_{i}x}e^{-ik_{j}x}\ dx=\left\{\begin{matrix}
1\left ( i=j \right )\\0\left ( i\neq j \right )
\end{matrix}\right.\tag{8}
\end{align*}

では、(8)式を計算してみましょう。

※虚数\(i\)と添え字の\(i\)が紛らわしいので、添え字を\(n\)や\(m\)で表すことにします。

(8)式を何も考えずに積分すると分母に\(m-n\)が来てしまうので、\(m=n\)と\(m\neq n\)に場合分けして積分します。

\(m=n\)のとき

\begin{align*}
\int _{-L}^{L}e^{ik_{m}x}e^{-ik_{n}x}\ dx =\int _{-L}^{L}=2L\tag{9}
\end{align*}

\(m\neq n\)のとき

\begin{align*}
\int _{-L}^{L}e^{ik_{m}x}e^{-ik_{n}x}\ dx =\bigg[\frac{1}{i(m-n)}e^{ik_{m}-k_{n}x}\bigg]^{L}_{-L} =0\tag{10}
\end{align*}

ゆえに、(9)(10)式をまとめると、

\begin{align*}
\int _{-L}^{L}e^{ik_{m}x}e^{-ik_{n}x}\ dx=\left\{\begin{matrix}
2L\left ( m=n \right )\\0\left (m \neq n \right )
\end{matrix}\right.\tag{11}
\end{align*}

もし、\(m=n\)のときに積分した値が１になるようにしたかったら、関数の集合を

\begin{align*}\{\frac{1}{\sqrt{2L}},\frac{1}{\sqrt{2L}}e^{ik_{1}x},\frac{1}{\sqrt{2L}}e^{ik_{2}x},\cdots,\frac{1}{\sqrt{2L}}e^{ik_{n}x},\cdots,\frac{1}{\sqrt{2L}}e^{-ik_{1}x},\frac{1}{\sqrt{2L}}e^{-ik_{2}x},\cdots,\frac{1}{\sqrt{2L}}e^{-ik_{n}x},\cdots\}\end{align*}

としておけば良いです。

\begin{align*}
\int _{-L}^{L}\frac{1}{\sqrt{2L}}e^{ik_{m}x}\frac{1}{\sqrt{2L}}e^{-ik_{n}x}\ dx=\left\{\begin{matrix}
1\left ( m=n \right )\\0\left (m \neq n \right )
\end{matrix}\right.
\end{align*}

複素フーリエ級数展開の係数\(c_{n}\)はどのように記述できるのか

ここから、フーリエ級数展開の係数\(c_{n}\)をどうやって求めることができるのかを示します。

求め方は簡単で(11)式の性質を使って、

  • 同じ関数\(m=n\)同士の掛け算の積分は値を持ち、
  • 異なる関数\(m\neq n\)同士の掛け算の積分は値が0になる

というのを利用します。

わかりやすくするために(7)式の和の部分を展開します。

例えば\(n\)番目の係数\(c_{n}\)が欲しい場合には、\(e^{ik_{n}x}\)を掛けて積分すると得ることができます。
※ただし、\(k_n=\frac{n\pi}{L}\)

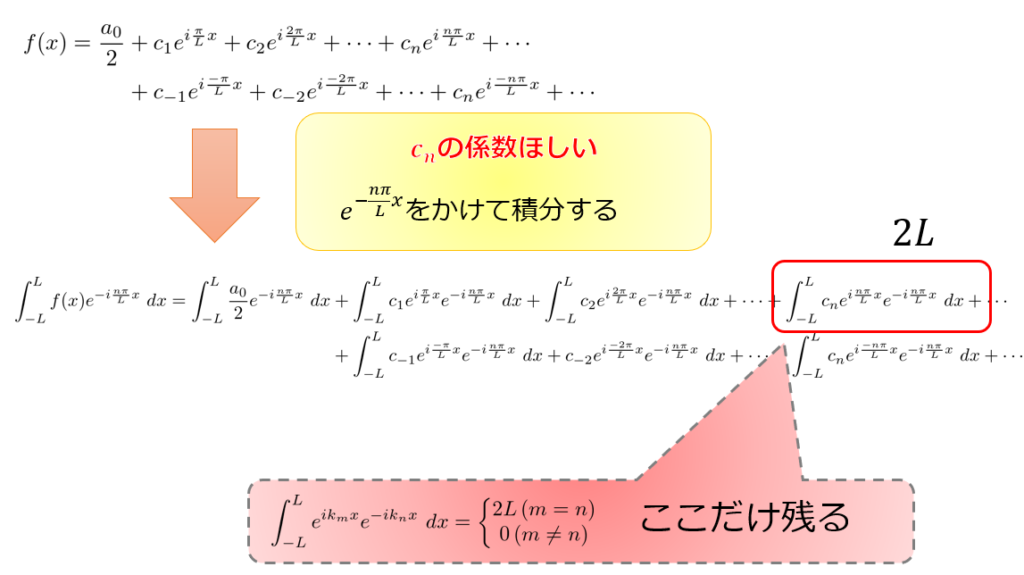
係数\(c_{n}\)は、

\begin{align*}
c_{n}=\frac{1}{2L}\int^{L}_{-L}f(x)e^{-ik_{n}x}\ dx\tag{12}
\end{align*}

まとめ

今までのところをまとめておきましょう。

フーリエ級数展開から複素フーリエ級数展開を考えました。

やったことの流れは以下です。

複素フーリエ級数展開

\(x\)の範囲を[\(-L\leq x\leq L\)]とし、関数の集合を、

\begin{align*}\{1,e^{ik_{1}x},e^{ik_{2}x},\cdots,e^{ik_{n}x},\cdots,e^{-ik_{1}x},e^{-ik_{2}x},\cdots,e^{-ik_{n}x},\cdots\}\end{align*}

※\(k_{n}=\frac{n\pi}{L}\)
として、任意関数\(f(x)\)は
\begin{align*}f(x)  = \sum_{n=-\infty}^{\infty}c_{n}e^{ik_{n}x}\end{align*}

と書けるよ、という話をしたいと思います。
これは複素フーリエ級数展開と呼ばれています。
係数\(c_{n}\)は、
\begin{align*}
c_{n}=\frac{1}{2L}\int^{L}_{-L}f(x)e^{-ik_{n}x}\ dx\tag{12}
\end{align*}

※\(e^{ik_{n}x}\)は\(2L\)周期関数ですので、任意関数\(f(x)\)も同じ\(2L\)周期関数に限った話であることに注意しましょう。

もし、\(m=n\)のときに積分した値が１になるようにしたかったら、関数の集合を

\begin{align*}\{\frac{1}{\sqrt{2L}},\frac{1}{\sqrt{2L}}e^{ik_{1}x},\frac{1}{\sqrt{2L}}e^{ik_{2}x},\cdots,\frac{1}{\sqrt{2L}}e^{ik_{n}x},\cdots,\frac{1}{\sqrt{2L}}e^{-ik_{1}x},\frac{1}{\sqrt{2L}}e^{-ik_{2}x},\cdots,\frac{1}{\sqrt{2L}}e^{-ik_{n}x},\cdots\}\end{align*}

としておけば良いです。

関連記事もどうぞ

COMMENT

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です