【フーリエ級数展開】直交関数系を使って任意関数を表そう。

この記事ではフーリエ級数展開について説明したいと思います！

前回の記事で以下のようことを書きました。

今、$x$の範囲を[$-L\leq x\leq L$]とします。※$x$の範囲は考えやすくするために[$-L\leq x\leq L$]とします。
関数の集合$\left \{f_{0}(x), f_{1}(x)\cdot\cdot\cdot,f_{n}(x)\right \}$を用意し、
これらの関数の集合を使って、

\begin{align*}
\int _{-L}^{L}f_{i}(x)f_{j}(x)dx=\left\{\begin{matrix}
1\left ( i=j \right )\\0\left ( i\neq j \right )
\end{matrix}\right.\tag{1}
\end{align*}

を満たすことを関数の直交性といいます。
これらの関数の集合を直交関数系といいます。
これらの関数の集合$\left \{f_{0}(x), f_{1}(x)\cdot\cdot\cdot,f_{n}(x)\right \}$を用いて任意の関数$f(x)$は、

\begin{align*}f(x)=a_{0}f_{0}(x)+a_{1}f_{1}(x)+a_{2}f_{2}(x)+\cdot\cdot\cdot+a_{n}f_{n}(x)=\sum^{n}_{i=0}a_{i}f_{i}(x)\tag{2}\end{align*}

前回の記事

直交関数系をベクトルの線形結合と類似して考えてみよう。

本記事では、

本記事の内容

$x$の範囲を[$-L\leq x\leq L$]とし、関数の集合を、

\begin{align*}\{1,\sin k_{1}x,\sin k_{2}x,\cdot\cdot\cdot\sin k_{n}x,\cdot\cdot\cdot,\cos k_{1}x,\cos k_{2}x,\cdot\cdot\cdot\cos k_{n}x,\cdot\cdot\cdot \}\end{align*}

※$k_{n}=\frac{n\pi}{L}$
として、任意関数$f(x)$は

\begin{align*}f(x) = \frac{a_{0}}{2}+\sum^{\infty}_{n=1}a_{n}\sin k_{n}x+\sum^{\infty}_{n=1}b_{n}\cos k_{n}x\tag{3}\end{align*}

と書けるよ、という話をしたいと思います。
（3）式はフーリエ級数展開と呼ばれています。
※サイン・コサインは$2L$周期関数ですので、任意関数$f(x)$も同じ$2L$周期関数に限った話であることに注意しましょう。

カマキリ

周期関数に限らない話は「フーリエ展開」でやるよ

「フーリエ変換」の記事はこちら

【フーリエ変換】非周期関数を考える。複素フーリエ級数展開の周期性を無限大にしよう。

【本記事の2つのポイント】

$-L\leq x\leq L$の範囲で、関数の集合$\{1,\sin k_{1}x,\sin k_{2}x,\cdot\cdot\cdot\sin k_{n}x,\cdot\cdot\cdot,\cos k_{1}x,\cos k_{2}x,\cdot\cdot\cdot\cos k_{n}x,\cdot\cdot\cdot \}$も関数の直交性を満たしていることを確認する。
任意関数が(3)式で書けるとき、フーリエ級数展開の係数$a_{n},b_{n}$はどのように記述されるのかを見る。

↓本記事の学習の流れ

道具としてのフーリエ解析

涌井良幸, 涌井貞美

2,560円(11/21 17:49時点)

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

物理現象のフーリエ解析 (ちくま学芸文庫)

小出昭一郎

1,430円(11/21 08:18時点)

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

サイン・コサインが直交性を満たしているかを確認する
フーリエ級数展開の係数$a_{n}$、$b_{n}$はどのように記述できるのか
まとめ
おまけ
1. 正規直交関数系にしたかったらどうする？
2. 次回のテーマ：本当にどんな$f(x)$もsin,cosの級数展開で記述できるのか？

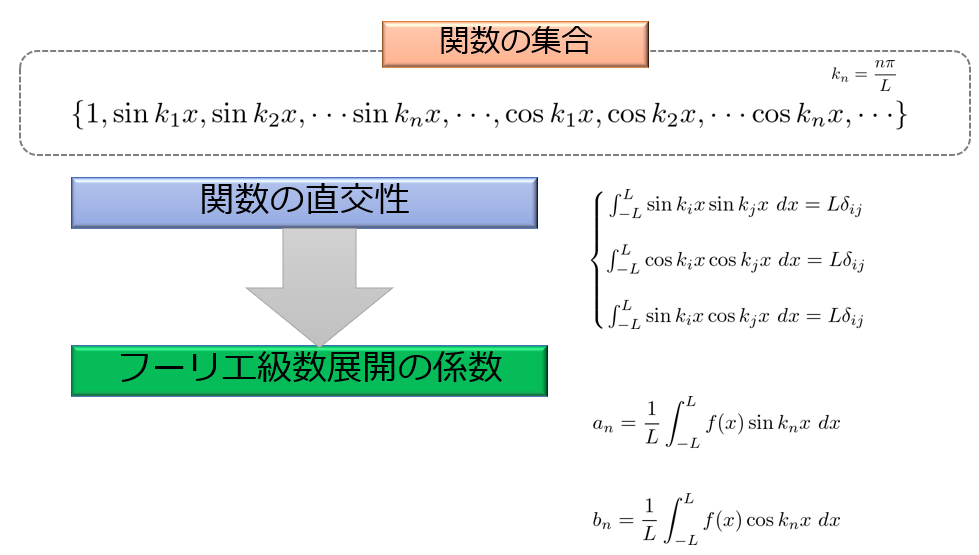
サイン・コサインが直交性を満たしているかを確認する

$-L\leq x\leq L$の範囲で、関数の集合、

\begin{align*}\{1,\sin k_{1}x,\sin k_{2}x,\cdot\cdot\cdot\sin k_{n}x,\cdot\cdot\cdot,\cos k_{1}x,\cos k_{2}x,\cdot\cdot\cdot\cos k_{n}x,\cdot\cdot\cdot \}\end{align*}

が、(1)式のような関数の直交性を満たしているかを確認しましょう(^^)/

上記の関数の集合から適当に2つ関数を選んで$x$の範囲で積分でして、(1)を満たすかを確認すれば良いということです。

つまり、

\begin{align*}
&\left\{\begin{matrix}
\int_{-L}^{L}\sin k_{i}x\sin k_{j}x \ dx\\
\\
\int_{-L}^{L}\cos k_{i}x\cos k_{j}x \ dx \\
\\
\int_{-L}^{L}\sin k_{i}x\cos k_{j}x \ dx
\end{matrix}\right.\tag{4}
\end{align*}

が$i\neq j$のとき0、$i=j$のときは0ではない数字(計算すると$L$)になるかどうかを確認すれば良いです。

(3)式全てを確認するのはめんどうなので、$\int_{-L}^{L}\sin k_{i}x\sin k_{j}x \ dx$だけ確認してみます。

\begin{align*}\int_{-L}^{L}\sin k_{i}x\sin k_{j}x\ dx\tag{5}\end{align*}

積分を実行するために、高校数学で習った以下の三角関数の公式を使います。

\begin{align*}
\left\{\begin{matrix}
\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta\\
\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta
\end{matrix}\right.\tag{6}
\end{align*}

今回は、(5)式の2つ目の式を使います。

\begin{align*}
\left\{\begin{matrix}
\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta\\
\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta
\end{matrix}\right.\tag{7}
\end{align*}

差し引きして、

\begin{align*}\sin(\alpha)\sin(\beta)=\frac{1}{2}\big(\cos(\alpha-\beta)-\cos(\alpha+\beta)\big)\tag{8}\end{align*}

となるので、(5)式に当てはめてみます。

\begin{align*}\frac{1}{2}\int_{-L}^{L}\big(\cos (k_{i}-k_{j})x-\cos (k_{i}+k_{j})x\big)\ dx\tag{9}\end{align*}

これを計算することになります。

※ここで、$k_{i}=\frac{i\pi}{L}$であることを用いると、

\begin{align*}\frac{1}{2}\int_{-L}^{L}\bigg(\cos \frac{i-j}{L}\pi x-\cos \frac{i+j}{L}\pi x\bigg)dx\tag{10}\end{align*}

これを積分することになるのですが、何も考えずに積分すると第一項を積分すると分母に$i-j$が来ることになりますので、

$i=j$と$i\neq j$で場合分けして計算しなければなりません。

(a)$i=j$のとき

\begin{align*}\frac{1}{2}\int_{-L}^{L}\bigg(\cos \frac{i-j}{L}\pi x-\cos \frac{i+j}{L}\pi x\bigg)dx \\
&=\frac{1}{2}\int_{-L}^{L}\big(1-\cos \frac{2i}{L}\pi x\big)dx \\
&=\frac{1}{2}\left \{\bigg[x\bigg]^{L}_{-L}-\bigg[\frac{L}{2i\pi}\sin \frac{2i}{L}x\bigg]^{L}_{-L}\right \}\\
& =L
\tag{11}\end{align*}

※$i$は整数なので積分すると0になるので、第一項だけが残ります。

(b)$i\neq j$のとき

\begin{align*}\frac{1}{2}\int_{-L}^{L}\bigg(\cos \frac{i-j}{L}\pi x-\cos \frac{i+j}{L}\pi x\bigg)dx \\
&=\frac{1}{2}\left \{\bigg[\frac{L}{i-j}\sin \frac{i-j}{L}\pi x\bigg]^{L}_{-L} -\bigg[\frac{L}{i-j}\sin \frac{i-j}{L}\pi x\bigg]^{L}_{-L}\right \} \\
&=0
\tag{12}\end{align*}

※$i,j$は整数なので、$\cos$の積分が0になります。

以上をまとめると、

\begin{align*}\int_{-L}^{L}\sin k_{i}x\sin k_{j}x \ dx =\left\{\begin{matrix}
L\left ( i=j \right )\\ 0\left ( i\neq j \right )
\end{matrix}\right. \tag{13}\end{align*}

(1)式のように$i=j$のときに積分すると1となるようにはなっていませんが、1になるかどうかは重要ではなく、

$i$と$j$が同じときには値があり、$i$と$j$が異なるときには値が0になるということです。

カマキリ

(3)式の残りの式は各自やりましょう(^^)/

というわけで、関数の集合

\begin{align*}\{1,\sin k_{1}x,\sin k_{2}x,\cdot\cdot\cdot\sin k_{n}x,\cdot\cdot\cdot,\cos k_{1}x,\cos k_{2}x,\cdot\cdot\cdot\cos k_{n}x,\cdot\cdot\cdot \}\end{align*}

が直交性を満たすことが確認できました。

ちなみに(3)の残りの結果は以下となります。

\begin{align*}
\left\{\begin{matrix}
\int_{-L}^{L}\sin k_{i}x\sin k_{j}x \ dx=L\delta_{ij}\\
\\
\int_{-L}^{L}\cos k_{i}x\cos k_{j}x \ dx =L\delta_{ij}\\
\\
\int_{-L}^{L}\sin k_{i}x\cos k_{j}x \ dx=L\delta_{ij}
\end{matrix}\right. \tag{19}
\end{align*}

フーリエ級数展開の係数$a_{n}$、$b_{n}$はどのように記述できるのか

関数の集合

\begin{align*}\{1,\sin k_{1}x,\sin k_{2}x,\cdot\cdot\cdot\sin k_{n}x,\cdot\cdot\cdot,\cos k_{1}x,\cos k_{2}x,\cdot\cdot\cdot\cos k_{n}x,\cdot\cdot\cdot \}\end{align*}

が直交性を見たることが確認できたので、前回の記事から任意関数$f(x$はこれらの関数の線形結合で書けます。

\begin{align*}f(x) = \frac{a_{0}}{2}+\sum^{\infty}_{n=1}a_{n}\sin k_{n}x+\sum^{\infty}_{n=1}b_{n}\cos k_{n}x\tag{14}\end{align*}

\begin{align*}f(x) =\sum^{\infty}_{n=0}a_{n}\sin k_{n}x+\sum^{\infty}_{n=0}b_{n}\cos k_{n}x\end{align*}

のように和のスタートを$n=0$としてもよいですが、$\sin, \cos$の和の両方に$n=0$が出てくるので(13)式は和の部分は$n=1$からにして$n=0$は外に出しています。

(14)式で$\frac{a_{0}}{2}$となっているのは、後ほど解説しますように便宜上そう書いてあるだけであって特に深い意味はありません。

ここから、フーリエ級数展開の係数$a_{n}$、$b_{n}$をどうやって求めることができるのかを示します。

求め方は簡単で(13)式の性質を使って、

同じ関数$i=j$同士の掛け算の積分は値を持ち、
異なる関数$j\neq j$同士の掛け算の積分は値が0になる

というのを利用します。

わかりやすくするために(14)式の和の部分を展開します。

例えば$n$番目の係数$a_{n}$が欲しい場合には、$\sin k_{n}x$を掛けて積分すると得ることができます。

つまり、

\begin{align*}
\int^{L}_{-L}a_{n}\sin k_{n}x\sin k_{n}x \ dx
\end{align*}

を計算して係数$a_{n}$を求めれば良いのです。

$\sin^2 k_{n}$の積分には2倍角の公式$\sin^2\theta=\frac{1+\cos2\theta}{2}$を使うことで積分が可能です。

\begin{align*}
\int^{L}_{-L}a_{n}\sin^2 k_{n} \ dx \\
&=\int^{L}_{-L}a_{n}\frac{1+\cos 2k_{n}x}{2} \ dx\\
&=a_{n}\frac{a_{n}}{2}\bigg[x+\frac{1}{2}\sin 2k_{n}x\bigg]^{L}_{-L}\\
&=L\tag{15}
\end{align*}

ゆえに係数$a_{n}$は、

\begin{align*}
a_{n}=\frac{1}{L}\int^{L}_{-L}f(x)\sin k_{n}x\ dx\tag{16}
\end{align*}

同様に係数$b_{n}$を求めたい場合は、$\cos k_{n}x$を掛けて積分すれば良いということになるので、各自試してみましょう(^^)/

結果はこのようになります。

\begin{align*}
b_{n}=\frac{1}{L}\int^{L}_{-L}f(x)\cos k_{n}x\ dx\tag{18}
\end{align*}

まとめ

今までのところをまとめておきましょう(^^)/

$x$の範囲を[$-L\leq x\leq L$]とし、関数の集合を、

\begin{align*}\{1,\sin k_{1}x,\sin k_{2}x,\cdot\cdot\cdot\sin k_{n}x,\cdot\cdot\cdot,\cos k_{1}x,\cos k_{2}x,\cdot\cdot\cdot\cos k_{n}x,\cdot\cdot\cdot \}\end{align*}

※$k_{n}=\frac{n\pi}{L}$
として、任意関数$f(x)$は

\begin{align*}f(x) = \frac{a_{0}}{2}+\sum^{\infty}_{n=1}a_{n}\sin k_{n}x+\sum^{\infty}_{n=1}b_{n}\cos k_{n}x\tag{3}\end{align*}

と書けます。
（3）式はフーリエ級数展開と呼ばれています。
関数の集合は、

の直交性を満たします。

※$\sin,\cos$が$2L$の周期関数であるので、$f(x)$も$2L$の周期関数

フーリエ級数展開の係数$a_{n},b_{n}$

\begin{align*}
a_{n}=\frac{1}{L}\int^{L}_{-L}f(x)\sin k_{n}x\ dx\tag{17}
\end{align*}

\begin{align*}
b_{n}=\frac{1}{L}\int^{L}_{-L}f(x)\cos k_{n}x\ dx\tag{18}
\end{align*}

おまけ

正規直交関数系にしたかったらどうする？

(19)式のように同じ三角関数の積同士の積分値が、

$i=j$なら$L$
$i\neq j$なら$0$

というように、$i=j$のときに$L$となっていて正規化されていません（１になっていません）。

$i=j$のときに積分した値が１にするためには、関数の集合を、

\begin{align*}\{\frac{1}{\sqrt{2L}},\frac{1}{\sqrt{L}}\sin k_{1}x,\frac{1}{\sqrt{L}}\sin k_{2}x,\cdot\cdot\cdot \frac{1}{\sqrt{L}}\sin k_{n}x,\cdot\cdot\cdot,\frac{1}{\sqrt{L}}\cos k_{1}x,\frac{1}{\sqrt{L}}\cos k_{2}x,\cdot\cdot\cdot \frac{1}{\sqrt{L}}\cos k_{n}x,\cdot\cdot\cdot \}\end{align*}

としておけば、

\begin{align*}
\left\{\begin{matrix}
\int_{-L}^{L}\frac{1}{\sqrt{L}}\sin k_{i}x\frac{1}{\sqrt{L}}\sin k_{j}x \ dx=\delta_{ij}\\
\\
\int_{-L}^{L}\frac{1}{\sqrt{L}}\cos k_{i}x\frac{1}{\sqrt{L}}\cos k_{j}x \ dx =\delta_{ij}\\
\\
\int_{-L}^{L}\frac{1}{\sqrt{L}}\sin k_{i}x\frac{1}{\sqrt{L}}\cos k_{j}x \ dx=\delta_{ij}
\end{matrix}\right. \tag{20}
\end{align*}

のように正規化することができます。