こんにちは(@t_kun_kamakiri)。
前回の記事では、「2次元のポアソン方程式」をGoogle Colab上のPythonで実装しました。
今回は、いよいよ２次元のナビエストークス方程式をPythonで実装します。
今回解析するのは「キャビティ流れ」と呼ばれる流れです。
式の詳細と数値計算の解き方については記事内で詳しく解説したいと思います(^^)/
カマキリ
流体解析は楽しいです(^^)/
本件の基本的な内容はこちらのサイトにそってやっていきます。
この記事ではこんな人を対象にしています。
こんな人が対象
- Pythonを使い始めたけどどう使うかわからない
- 流体の数値計算をはじめて勉強する人
いよいよ本記事シリーズの最終目標であるナビエストークス方程式をPythonで実装するというところまで来ました！
今回の内容はこちら
２次元のナビエストークス方程式の「キャビティ流れ」をPythonで実装
カマキリ
今日もゆる～く学びます(^^)/
解くべき方程式の確認（ナビエストークス方程式とポアソン方程式）
まずは、今回「解くべき方程式」と「変数」が何かを確認しておきましょう。
非圧縮性流体として現象を取り扱う場合には、基本的には以下の2つの式を連立して解きます。
実際の流れは、すべての現象が(1)(2)式というわけではないです。
「ニュートン流体」「非圧縮の流れ（近似）」としているとても限定的な流れであることを理解しておきましょう。
もっと詳しく勉強したい方は☟こちらの記事を参考にしてください。
もっと詳しく勉強したい方は☟こちらの記事を参考にしてください。
あわせて読みたい
今回は、2次元で計算を行うため少々くどいですが、成分ごとの式を書き下すことにします。
未知数は、\(\boldsymbol{v}\)の2つと圧力\(p\)の合計3つです。なので、原理的に未知数である物理量は全て求まることになります。それを各時刻で求めていけば良いという事になります。
しかし、言葉で簡単に言っても、特殊な境界条件や近似を用いないとナビエストークス方程式は解析的に取り扱うことができないのです。つまり、ナビエストークス方程式には一般解が見つかっていないので、実際には数値計算を使って偏微分方程式を取り扱うしかないのが現状です。
しかし、連立方程式を解けばいいと言われてもちょっと困った・・・
なぜなら、(3)(4)式で求めた流速は(5)式を満たす必要があります。
そのように流速を選びながら圧力を同時に決めなければなりません。
考えただけでもちょっと工夫が必要ですよね。。
そこで、以下のようにして考えを改めます。
圧力に関しては非圧縮条件を満たすようにポアソン方程式を解きつつ、求めた圧力に関してナビエストークス方程式を解き流速を求めるという手法をとります。
言葉で説明してもよくわからないかもしれないので、実際にやります(^^)/
(3)式を\(x\)で偏微分
\begin{align*}
&\frac{\partial }{\partial x}\frac{\partial u}{\partial t}+\frac{\partial u}{\partial x}\frac{\partial u}{\partial x}+u\frac{\partial^2 u}{\partial x^2}+ \frac{\partial v}{\partial x}\frac{\partial u}{\partial y}+v\frac{\partial^2 u}{\partial x\partial y} \\
&= -\frac{1}{\rho}\frac{\partial^2 p}{\partial x^2}+\nu \frac{\partial }{\partial x}\left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2} \right)\tag{6}
\end{align*}
&\frac{\partial }{\partial x}\frac{\partial u}{\partial t}+\frac{\partial u}{\partial x}\frac{\partial u}{\partial x}+u\frac{\partial^2 u}{\partial x^2}+ \frac{\partial v}{\partial x}\frac{\partial u}{\partial y}+v\frac{\partial^2 u}{\partial x\partial y} \\
&= -\frac{1}{\rho}\frac{\partial^2 p}{\partial x^2}+\nu \frac{\partial }{\partial x}\left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2} \right)\tag{6}
\end{align*}
(4)式を\(y\)で偏微分
\begin{align*}
&\frac{\partial }{\partial y}\frac{\partial v}{\partial t}+\frac{\partial u}{\partial y}\frac{\partial v}{\partial x}+u\frac{\partial^2 v}{\partial y\partial x}+ \frac{\partial v}{\partial y}\frac{\partial v}{\partial y}+v\frac{\partial^2 v}{\partial x\partial y^2} \\
&=-\frac{1}{\rho}\frac{\partial^2 p}{\partial y^2}+\nu \frac{\partial }{\partial y}\left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2} \right)\tag{7}
\end{align*}
&\frac{\partial }{\partial y}\frac{\partial v}{\partial t}+\frac{\partial u}{\partial y}\frac{\partial v}{\partial x}+u\frac{\partial^2 v}{\partial y\partial x}+ \frac{\partial v}{\partial y}\frac{\partial v}{\partial y}+v\frac{\partial^2 v}{\partial x\partial y^2} \\
&=-\frac{1}{\rho}\frac{\partial^2 p}{\partial y^2}+\nu \frac{\partial }{\partial y}\left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2} \right)\tag{7}
\end{align*}
このようにして辺々足すと左辺は以下のようになります。
\begin{align*}
\frac{\partial u}{\partial x}\frac{\partial u}{\partial x}+2\frac{\partial u}{\partial y}\frac{\partial v}{\partial x}+\frac{\partial v}{\partial y}\frac{\partial v}{\partial y}+u\frac{\partial u}{\partial x^2}+v\frac{\partial v}{\partial y^2}\\
+\frac{\partial}{\partial t}\bigg(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\bigg)+u\frac{\partial^2 u}{\partial x^2}+v\frac{\partial^2 u}{\partial x\partial y}+v\frac{\partial^2 v}{\partial y^2}+u\frac{\partial^2 v}{\partial y\partial x}
\end{align*}
\frac{\partial u}{\partial x}\frac{\partial u}{\partial x}+2\frac{\partial u}{\partial y}\frac{\partial v}{\partial x}+\frac{\partial v}{\partial y}\frac{\partial v}{\partial y}+u\frac{\partial u}{\partial x^2}+v\frac{\partial v}{\partial y^2}\\
+\frac{\partial}{\partial t}\bigg(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\bigg)+u\frac{\partial^2 u}{\partial x^2}+v\frac{\partial^2 u}{\partial x\partial y}+v\frac{\partial^2 v}{\partial y^2}+u\frac{\partial^2 v}{\partial y\partial x}
\end{align*}
最後の4項をまとめると、
\begin{align*}
u\frac{\partial^2 u}{\partial x^2}+v\frac{\partial^2 u}{\partial x\partial y}+v\frac{\partial^2 v}{\partial y^2}+u\frac{\partial^2 v}{\partial y\partial x}=u\frac{\partial}{\partial x}\bigg(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\bigg)+v\frac{\partial}{\partial y}\bigg(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\bigg)
\end{align*}
u\frac{\partial^2 u}{\partial x^2}+v\frac{\partial^2 u}{\partial x\partial y}+v\frac{\partial^2 v}{\partial y^2}+u\frac{\partial^2 v}{\partial y\partial x}=u\frac{\partial}{\partial x}\bigg(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\bigg)+v\frac{\partial}{\partial y}\bigg(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\bigg)
\end{align*}
非圧縮条件$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$を使えば0になります。しかし、数値計算上の誤差も考慮して解き進めたいので、$\frac{\partial}{\partial t}\big(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\big)$は残しておきます。しかし、$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}$をさらに空間微分した$u\frac{\partial}{\partial x}\bigg(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\bigg)+v\frac{\partial}{\partial y}\big(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\big)$は０と考えて消去します。
\begin{align*}
\frac{\partial^2 p}{\partial x^2}+\frac{\partial^2 p}{\partial y^2} = -\rho\left(\frac{\partial}{\partial t}\bigg(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\bigg)+\frac{\partial u}{\partial x}\frac{\partial u}{\partial x}+2\frac{\partial u}{\partial y}\frac{\partial v}{\partial x}+\frac{\partial v}{\partial y}\frac{\partial v}{\partial y} \right)\tag{8}
\end{align*}
\frac{\partial^2 p}{\partial x^2}+\frac{\partial^2 p}{\partial y^2} = -\rho\left(\frac{\partial}{\partial t}\bigg(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\bigg)+\frac{\partial u}{\partial x}\frac{\partial u}{\partial x}+2\frac{\partial u}{\partial y}\frac{\partial v}{\partial x}+\frac{\partial v}{\partial y}\frac{\partial v}{\partial y} \right)\tag{8}
\end{align*}
計算はだるいですが、一度やってみてください。
つまり、(3)(4)(5)を解く代わりに以下の式を解けばよいという事になります。
速度については、ナビエストークス方程式を解きつつ、圧力に対してポアソン方程式を連立させながら解くという事になります。
ポアソン方程式の解き方については、以下の記事で解説していますのでまだ読んでいない方はお読みください_(._.)_
では、解くべき方程式がわかったところで、(3)(4)(8.1)(8.2)を離散化して数値計算ができる状態にします。
解くべき方程式の離散化
【2次元での計算】※実際に解く方程式
ナビエストークス方程式
\begin{align*}
& \frac{u_{i,j}^{n+1}-u_{i,j}^{n}}{\Delta t}+u_{i,j}^{n}\frac{u_{i,j}^{n}-u_{i-1,j}^{n}}{\Delta x}+v_{i,j}^{n}\frac{u_{i,j}^{n}-u_{i,j-1}^{n}}{\Delta y} = \\
& \qquad -\frac{1}{\rho}\frac{p_{i+1,j}^{n+1}-p_{i-1,j}^{n+1}}{2\Delta x}+\nu\left(\frac{u_{i+1,j}^{n}-2u_{i,j}^{n}+u_{i-1,j}^{n}}{\Delta
x^2}+\frac{u_{i,j+1}^{n}-2u_{i,j}^{n}+u_{i,j-1}^{n}}{\Delta y^2}\right)\tag{9}
\end{align*}
& \frac{u_{i,j}^{n+1}-u_{i,j}^{n}}{\Delta t}+u_{i,j}^{n}\frac{u_{i,j}^{n}-u_{i-1,j}^{n}}{\Delta x}+v_{i,j}^{n}\frac{u_{i,j}^{n}-u_{i,j-1}^{n}}{\Delta y} = \\
& \qquad -\frac{1}{\rho}\frac{p_{i+1,j}^{n+1}-p_{i-1,j}^{n+1}}{2\Delta x}+\nu\left(\frac{u_{i+1,j}^{n}-2u_{i,j}^{n}+u_{i-1,j}^{n}}{\Delta
x^2}+\frac{u_{i,j+1}^{n}-2u_{i,j}^{n}+u_{i,j-1}^{n}}{\Delta y^2}\right)\tag{9}
\end{align*}
\begin{align*}
&\frac{v_{i,j}^{n+1}-v_{i,j}^{n}}{\Delta t}+u_{i,j}^{n}\frac{v_{i,j}^{n}-v_{i-1,j}^{n}}{\Delta x}+v_{i,j}^{n}\frac{v_{i,j}^{n}-v_{i,j-1}^{n}}{\Delta y} = \\
& \qquad -\frac{1}{\rho}\frac{p_{i,j+1}^{n+1}-p_{i,j-1}^{n+1}}{2\Delta y}+\nu\left(\frac{v_{i+1,j}^{n}-2v_{i,j}^{n}+v_{i-1,j}^{n}}{\Delta x^2}+\frac{v_{i,j+1}^{n}-2v_{i,j}^{n}+v_{i,j-1}^{n}}{\Delta y^2}\right)\tag{10}
\end{align*}
&\frac{v_{i,j}^{n+1}-v_{i,j}^{n}}{\Delta t}+u_{i,j}^{n}\frac{v_{i,j}^{n}-v_{i-1,j}^{n}}{\Delta x}+v_{i,j}^{n}\frac{v_{i,j}^{n}-v_{i,j-1}^{n}}{\Delta y} = \\
& \qquad -\frac{1}{\rho}\frac{p_{i,j+1}^{n+1}-p_{i,j-1}^{n+1}}{2\Delta y}+\nu\left(\frac{v_{i+1,j}^{n}-2v_{i,j}^{n}+v_{i-1,j}^{n}}{\Delta x^2}+\frac{v_{i,j+1}^{n}-2v_{i,j}^{n}+v_{i,j-1}^{n}}{\Delta y^2}\right)\tag{10}
\end{align*}
ポアソン方程式※連続の式（非圧縮条件）
\begin{align*}
\frac{p_{i+1,j}^{n+1}-2p_{i,j}^{n+1}+p_{i-1,j}^{n}}{\Delta x^2}+\frac{p_{i,j+1}^{n+1}-2p_{i,j}^{n+1}+p_{i,j-1}^{n+1}}{\Delta y^2} = b_{i,j}^{n}\tag{11.1}
\end{align*}
\frac{p_{i+1,j}^{n+1}-2p_{i,j}^{n+1}+p_{i-1,j}^{n}}{\Delta x^2}+\frac{p_{i,j+1}^{n+1}-2p_{i,j}^{n+1}+p_{i,j-1}^{n+1}}{\Delta y^2} = b_{i,j}^{n}\tag{11.1}
\end{align*}
\begin{align*}
b_{i,j}^{n} = \rho \left[ \frac{1}{\Delta t}\left(\frac{u_{i+1,j}-u_{i-1,j}}{2\Delta x}+\frac{v_{i,j+1}-v_{i,j-1}}{2\Delta y}\right)\\
-\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}\\
– 2\frac{u_{i,j+1}^{n}-u_{i,j-1}^{n}}{2\Delta y}\frac{v_{i+1,j}^{n}-v_{i-1,j}^{n}}{2\Delta x}\\
– \frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\right]\tag{11.2}
\end{align*}
b_{i,j}^{n} = \rho \left[ \frac{1}{\Delta t}\left(\frac{u_{i+1,j}-u_{i-1,j}}{2\Delta x}+\frac{v_{i,j+1}-v_{i,j-1}}{2\Delta y}\right)\\
-\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}\\
– 2\frac{u_{i,j+1}^{n}-u_{i,j-1}^{n}}{2\Delta y}\frac{v_{i+1,j}^{n}-v_{i-1,j}^{n}}{2\Delta x}\\
– \frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\right]\tag{11.2}
\end{align*}
※非圧縮過程なので$\nabla \cdot \boldsymbol{v}=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$
どういった離散化をしているのかを以下でまとめておきました。
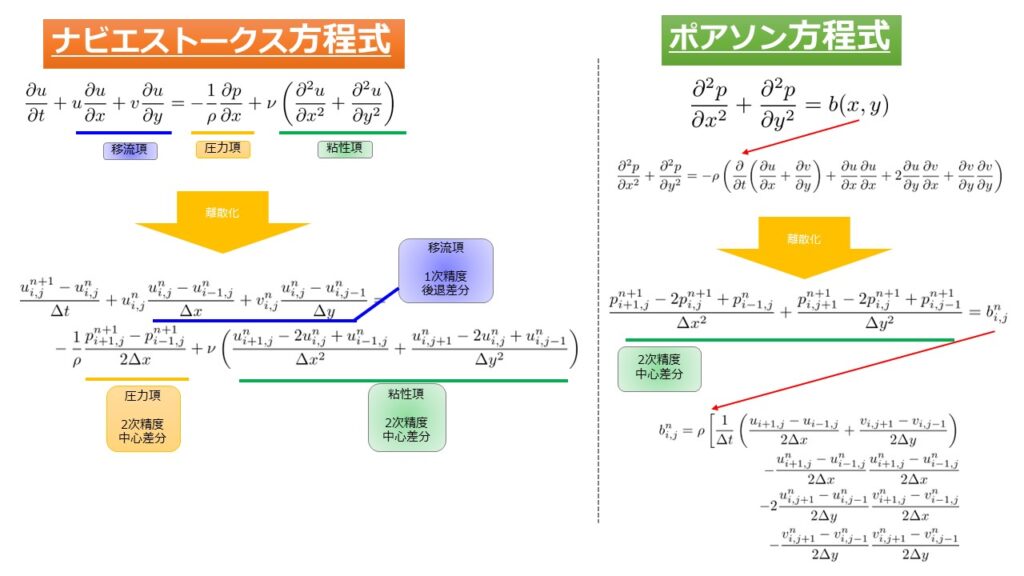
これで離散化は完了ですが、知りたいのは\(n+1\)ステップでの格子点\(i,j\)の流速\(u^{n+1}_{ij}\)、\(v^{n+1}_{ij}\)、圧力\(p^{n+1}_{ij}\)ですので、
以下のように式変形します。
【2次元での計算】※実際に解く方程式
ナビエストークス方程式
\begin{align*}
u_{i,j}^{n+1} = u_{i,j}^{n} & – u_{i,j}^{n} \frac{\Delta t}{\Delta x} \left(u_{i,j}^{n}-u_{i-1,j}^{n}\right) – v_{i,j}^{n} \frac{\Delta t}{\Delta y} \left(u_{i,j}^{n}-u_{i,j-1}^{n}\right) \\
& – \frac{\Delta t}{\rho 2\Delta x} \left(p_{i+1,j}^{n}-p_{i-1,j}^{n}\right) \\
& + \nu \left(\frac{\Delta t}{\Delta x^2} \left(u_{i+1,j}^{n}-2u_{i,j}^{n}+u_{i-1,j}^{n}\right) + \frac{\Delta t}{\Delta y^2}
\left(u_{i,j+1}^{n}-2u_{i,j}^{n}+u_{i,j-1}^{n}\right)\right)\tag{12}
\end{align*}
u_{i,j}^{n+1} = u_{i,j}^{n} & – u_{i,j}^{n} \frac{\Delta t}{\Delta x} \left(u_{i,j}^{n}-u_{i-1,j}^{n}\right) – v_{i,j}^{n} \frac{\Delta t}{\Delta y} \left(u_{i,j}^{n}-u_{i,j-1}^{n}\right) \\
& – \frac{\Delta t}{\rho 2\Delta x} \left(p_{i+1,j}^{n}-p_{i-1,j}^{n}\right) \\
& + \nu \left(\frac{\Delta t}{\Delta x^2} \left(u_{i+1,j}^{n}-2u_{i,j}^{n}+u_{i-1,j}^{n}\right) + \frac{\Delta t}{\Delta y^2}
\left(u_{i,j+1}^{n}-2u_{i,j}^{n}+u_{i,j-1}^{n}\right)\right)\tag{12}
\end{align*}
\begin{align*}
v_{i,j}^{n+1} = v_{i,j}^{n} & – u_{i,j}^{n} \frac{\Delta t}{\Delta x} \left(v_{i,j}^{n}-v_{i-1,j}^{n}\right) – v_{i,j}^{n} \frac{\Delta t}{\Delta y} \left(v_{i,j}^{n}-v_{i,j-1}^{n})\right) \\
& – \frac{\Delta t}{\rho 2\Delta y} \left(p_{i,j+1}^{n+1}-p_{i,j-1}^{n+1}\right) \\
& + \nu \left(\frac{\Delta t}{\Delta x^2} \left(v_{i+1,j}^{n}-2v_{i,j}^{n}+v_{i-1,j}^{n}\right) + \frac{\Delta t}{\Delta y^2}
\left(v_{i,j+1}^{n}-2v_{i,j}^{n}+v_{i,j-1}^{n}\right)\right)\tag{13}
\end{align*}
v_{i,j}^{n+1} = v_{i,j}^{n} & – u_{i,j}^{n} \frac{\Delta t}{\Delta x} \left(v_{i,j}^{n}-v_{i-1,j}^{n}\right) – v_{i,j}^{n} \frac{\Delta t}{\Delta y} \left(v_{i,j}^{n}-v_{i,j-1}^{n})\right) \\
& – \frac{\Delta t}{\rho 2\Delta y} \left(p_{i,j+1}^{n+1}-p_{i,j-1}^{n+1}\right) \\
& + \nu \left(\frac{\Delta t}{\Delta x^2} \left(v_{i+1,j}^{n}-2v_{i,j}^{n}+v_{i-1,j}^{n}\right) + \frac{\Delta t}{\Delta y^2}
\left(v_{i,j+1}^{n}-2v_{i,j}^{n}+v_{i,j-1}^{n}\right)\right)\tag{13}
\end{align*}
ポアソン方程式※連続の式（非圧縮条件）
\begin{align*}
p_{i,j}^{n+1}=\frac{(p_{i+1,j}^{n+1}+p_{i-1,j}^{n+1})\Delta y^2+(p_{i,j+1}^{n+1}+p_{i,j-1}^{n+1})\Delta x^2-b_{i,j}^{n}\Delta x^2\Delta y^2}{2(\Delta x^2+\Delta y^2)}
\tag{14.1}
\end{align*}
p_{i,j}^{n+1}=\frac{(p_{i+1,j}^{n+1}+p_{i-1,j}^{n+1})\Delta y^2+(p_{i,j+1}^{n+1}+p_{i,j-1}^{n+1})\Delta x^2-b_{i,j}^{n}\Delta x^2\Delta y^2}{2(\Delta x^2+\Delta y^2)}
\tag{14.1}
\end{align*}
\begin{align*}
b_{i,j}^{n} = \rho\left[ \frac{1}{\Delta t}\left(\frac{u_{i+1,j}-u_{i-1,j}}{2\Delta x}+\frac{v_{i,j+1}-v_{i,j-1}}{2\Delta y}\right) -\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}\\
-2\frac{u_{i,j+1}^{n}-u_{i,j-1}^{n}}{2\Delta y}\frac{v_{i+1,j}^{n}-v_{i-1,j}^{n}}{2\Delta x}-\\
\frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\right]\tag{14.2}
\end{align*}
b_{i,j}^{n} = \rho\left[ \frac{1}{\Delta t}\left(\frac{u_{i+1,j}-u_{i-1,j}}{2\Delta x}+\frac{v_{i,j+1}-v_{i,j-1}}{2\Delta y}\right) -\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}\\
-2\frac{u_{i,j+1}^{n}-u_{i,j-1}^{n}}{2\Delta y}\frac{v_{i+1,j}^{n}-v_{i-1,j}^{n}}{2\Delta x}-\\
\frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\right]\tag{14.2}
\end{align*}
では、これらを数値計算で解いていきましょう。
その前に、初期状態と境界条件を設定
数値計算をはじめるまえに、初期状態と境界条件を設定する必要があります。
【初期状態】
- \(u, v, p = 0\)
【境界条件】
- \(u=1\) at \(y=2\)
- \(u, v=0\) その他
- \(\frac{\partial p}{\partial y}=0\) at \(y=0\)
- \(p=0\) at \(y=2\)
- \(\frac{\partial p}{\partial x}=0\) at \(x=0,2\)
言葉だけではよくわからないかと思いますので、絵を作成しました。
今回解析するのは「キャビティ流れ」と呼ばれる流れです。
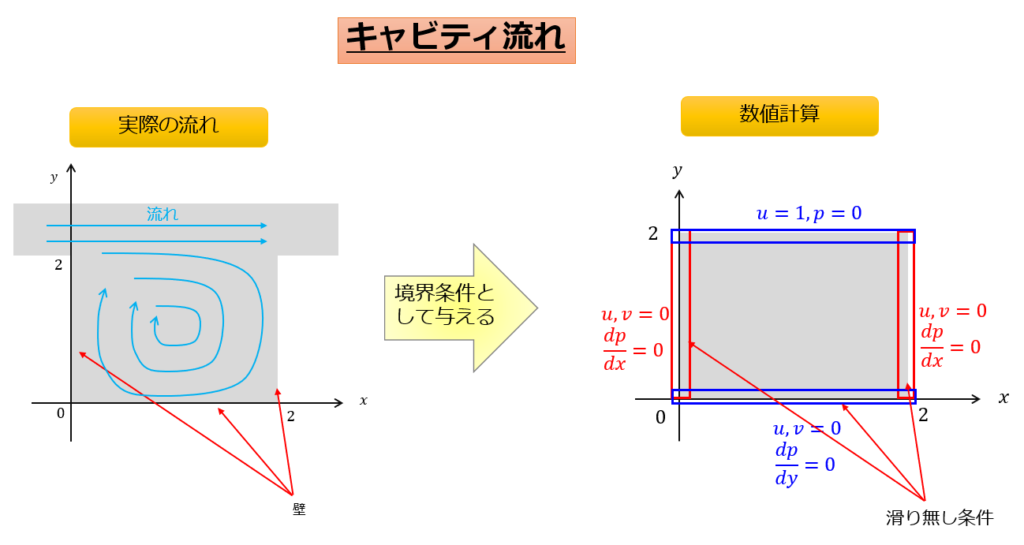
※ちなみに、圧力の基準圧を\(p=0\)としています。
なので、境界条件として\(y=0\)の圧力は\(p=0\)としています。
非圧縮条件で式を解く場合は、圧力の微分の項のみしか意味がないので、基準値は何でもいいんですよね。だから、もし考えている系の基準圧を大気圧（101.25Paくらい）としている場合に、わざわざ境界条件を\(p=101.325kPa\)とする必要はありません。
境界条件に\(p=0\)としておいて、計算された圧力分布は基準圧に対してどうなのかを考えればいいだけです。
（基準圧が\(p=101.325kPa\)なら、分布に\(p=101.325kPa\)を足せばいいだけという意味です）
流体解析に関する境界条件の考え方は非常に見ずかしいので、扱う現象に応じて自身で境界条件を考える必要があります。
ここでは、詳しくは解説しませんが（体系的に解説できるほどの知識もないですが_(._.)_）以下の記事が参考になると思います。
境界条件に関する記事はこちら
では、以下で実際にナビエストークス方程式とポアソン方程式を連立させながらGoogle Colaboratoryを使ってPythonのコードを書いていきましょう。
キャビティ流れを解く手順（フロー）
ひとつひとつ解説をしながらコードを書いていきます。
※関数にまとめておいた方がいい部分は関数にまとめます。
今回行う数値計算の解く手順は以下のフローに従っています。
これは「MAC（Marker And Cell）法」と呼ばれる非圧縮流体の解析手法の一種です。
ナビエストークス方程式、およびナビエストークス方程式の発散と連続の式から得られる圧力方程式を連立して計算を行います。
ナビエストークス方程式、およびナビエストークス方程式の発散と連続の式から得られる圧力方程式を連立して計算を行います。
Pythonで実装
【ポイント】
必要なライブラリをインポートする。
必要なライブラリをインポートする。
コードを以下のように書きます。
1 2 3 4 | import numpy as np from matplotlib import pyplot as plt from matplotlib import cm from mpl_toolkits.mplot3d import Axes3D |
NumpyとMatplotlibをインポートします。
記述ミスがなければエラーなく進みます。
【ポイント】
- 条件設定（空間領域、時間刻み）
- 初期状態の設定
- 境界条件の設定
コードを以下のように書きます。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | #条件設定 nx = 41 ny = 41 nt = 500 nit = 50 c = 1 dx = 2 / (nx - 1) dy = 2 / (ny - 1) x = np.linspace(0, 2, nx) y = np.linspace(0, 2, ny) X, Y = np.meshgrid(x, y) rho = 1 nu = .1 dt = .001 #初期状態 u = np.zeros((ny, nx)) v = np.zeros((ny, nx)) p = np.zeros((ny, nx)) b = np.zeros((ny, nx)) |
※初期状態は実際に解く際にももう一回定義しなおすので、ここでは書かなくても良いですが・・・
ポアソン方程式の解く部分は結構煩雑なので、まずは\(b^{n}_{ij}\)に関しては以下のように関数にまとめておきます。
【ポイント】
の関数を作成する。
\begin{align*}
b_{i,j}^{n} = \rho\left[ \frac{1}{\Delta t}\left(\frac{u_{i+1,j}-u_{i-1,j}}{2\Delta x}+\frac{v_{i,j+1}-v_{i,j-1}}{2\Delta y}\right) -\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}\\
-2\frac{u_{i,j+1}^{n}-u_{i,j-1}^{n}}{2\Delta y}\frac{v_{i+1,j}^{n}-v_{i-1,j}^{n}}{2\Delta x}-\\
\frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\right]\tag{14.2}
\end{align*}
b_{i,j}^{n} = \rho\left[ \frac{1}{\Delta t}\left(\frac{u_{i+1,j}-u_{i-1,j}}{2\Delta x}+\frac{v_{i,j+1}-v_{i,j-1}}{2\Delta y}\right) -\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}\\
-2\frac{u_{i,j+1}^{n}-u_{i,j-1}^{n}}{2\Delta y}\frac{v_{i+1,j}^{n}-v_{i-1,j}^{n}}{2\Delta x}-\\
\frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\right]\tag{14.2}
\end{align*}
の関数を作成する。
コードを以下のように書きます。
1 2 3 4 5 6 7 8 9 10 11 | def build_up_b(b, rho, dt, u, v, dx, dy): b[1:-1, 1:-1] = (rho * (1 / dt * ((u[1:-1, 2:] - u[1:-1, 0:-2]) / (2 * dx) + (v[2:, 1:-1] - v[0:-2, 1:-1]) / (2 * dy)) - ((u[1:-1, 2:] - u[1:-1, 0:-2]) / (2 * dx))**2 - 2 * ((u[2:, 1:-1] - u[0:-2, 1:-1]) / (2 * dy) * (v[1:-1, 2:] - v[1:-1, 0:-2]) / (2 * dx))- ((v[2:, 1:-1] - v[0:-2, 1:-1]) / (2 * dy))**2)) return b |
そして、ポアソン方程式本体は、以下のように関数としておきます。
コードを以下のように書きます。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | def pressure_poisson(p, dx, dy, b): pn = np.empty_like(p) pn = p.copy() for q in range(nit): pn = p.copy() p[1:-1, 1:-1] = (((pn[1:-1, 2:] + pn[1:-1, 0:-2]) * dy**2 + (pn[2:, 1:-1] + pn[0:-2, 1:-1]) * dx**2) / (2 * (dx**2 + dy**2)) - dx**2 * dy**2 / (2 * (dx**2 + dy**2)) * b[1:-1,1:-1]) p[:, -1] = p[:, -2] # dp/dx = 0 at x = 2 p[0, :] = p[1, :] # dp/dy = 0 at y = 0 p[:, 0] = p[:, 1] # dp/dx = 0 at x = 0 p[-1, :] = 0 # p = 0 at y = 2 return p |
前回の記事でも解説しましたが、ポアソン方程式では「反復計算」による計算を行って圧力を求めています。
収束判定の方法は色々アイデアがるのですが、「ある値以下になったら収束する方法」か「ある回数反復計算したら収束したとみなす方法」のどちらかが主にやられる手法です。
今回は「nit = 50」として、50回反復計算したら収束している（であろう）として、ポアソン方程式から圧力を求めています。
では、メインの流速を求める部分を以下のように関数にまとめておきます。
コードを以下のように書きます。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 | def cavity_flow(nt, u, v, dt, dx, dy, p, rho, nu): un = np.empty_like(u) vn = np.empty_like(v) b = np.zeros((ny, nx)) for n in range(nt): un = u.copy() vn = v.copy() b = build_up_b(b, rho, dt, u, v, dx, dy) p = pressure_poisson(p, dx, dy, b) u[1:-1, 1:-1] = (un[1:-1, 1:-1]- un[1:-1, 1:-1] * dt / dx * (un[1:-1, 1:-1] - un[1:-1, 0:-2]) - vn[1:-1, 1:-1] * dt / dy * (un[1:-1, 1:-1] - un[0:-2, 1:-1]) - dt / (2 * rho * dx) * (p[1:-1, 2:] - p[1:-1, 0:-2]) + nu * (dt / dx**2 * (un[1:-1, 2:] - 2 * un[1:-1, 1:-1] + un[1:-1, 0:-2]) + dt / dy**2 * (un[2:, 1:-1] - 2 * un[1:-1, 1:-1] + un[0:-2, 1:-1]))) v[1:-1,1:-1] = (vn[1:-1, 1:-1] - un[1:-1, 1:-1] * dt / dx * (vn[1:-1, 1:-1] - vn[1:-1, 0:-2]) - vn[1:-1, 1:-1] * dt / dy * (vn[1:-1, 1:-1] - vn[0:-2, 1:-1]) - dt / (2 * rho * dy) * (p[2:, 1:-1] - p[0:-2, 1:-1]) + nu * (dt / dx**2 * (vn[1:-1, 2:] - 2 * vn[1:-1, 1:-1] + vn[1:-1, 0:-2]) + dt / dy**2 * (vn[2:, 1:-1] - 2 * vn[1:-1, 1:-1] + vn[0:-2, 1:-1]))) u[0, :] = 0 u[:, 0] = 0 u[:, -1] = 0 u[-1, :] = 1 # set velocity on cavity lid equal to 1 v[0, :] = 0 v[-1, :] = 0 v[:, 0] = 0 v[:, -1] = 0 return u, v, p |
これで、主要な関数の作成は終了です。
では、初期状態を用意して上で用意した関数を使ってナビエストークス方程式を解いてみましょう。
【ポイント】
初期状態とタイムステップ数を指定して解く。
初期状態とタイムステップ数を指定して解く。
コードを以下のように書きます。
1 2 3 4 5 6 | u = np.zeros((ny, nx)) v = np.zeros((ny, nx)) p = np.zeros((ny, nx)) b = np.zeros((ny, nx)) nt = 100 u, v, p = cavity_flow(nt, u, v, dt, dx, dy, p, rho, nu) |
「nt = 100」として100ステップだけ計算させました。
エラーなく実行できれば、何も出力されませんが、u,vの流速分布がキャビティ流れになっています。
結果の可視化にはMatplotlibを使います。
Matplotlibで結果を可視化する
結果の可視化は色々あるのですが、今回は以下の4つを見たいと思います。
【ポイント】
- 圧力のコンターを見る
- 圧力の等高線を見る
- 流速ベクトルを見る
- 流線を見る
１．圧力のコンターを見る
コードを以下のように書きます。
1 2 3 4 5 | #figオブジェクトで図の枠を用意 fig = plt.figure(figsize=(11,7), dpi=100) plt.contourf(X, Y, p, alpha=0.5, cmap=cm.viridis) plt.colorbar() |
【結果】
２．圧力の等高線を見る
コードを以下のように書きます。
1 2 3 4 5 6 | #圧力の等高線を描く #figオブジェクトで図の枠を用意 fig = plt.figure(figsize=(8,5), dpi=100) plt.contour(X, Y, p, cmap=cm.viridis) |
【結果】
ちなみにコンターと等高線を一緒に書くこともできます。
1 2 3 4 5 6 | #figオブジェクトで図の枠を用意 fig = plt.figure(figsize=(11,7), dpi=100) plt.contourf(X, Y, p, alpha=0.5, cmap=cm.viridis) plt.colorbar() plt.contour(X, Y, p, cmap=cm.viridis) |
【結果】
これで圧力の分布が可視化されました(^^)/
次に流速についても可視化してみましょう。
３．流速ベクトルを見る
コードを以下のように書きます。
1 2 3 4 | #流速ベクトルを表示 plt.quiver(X[::2, ::2], Y[::2, ::2], u[::2, ::2], v[::2, ::2]) plt.xlabel('X') plt.ylabel('Y'); |
【結果】
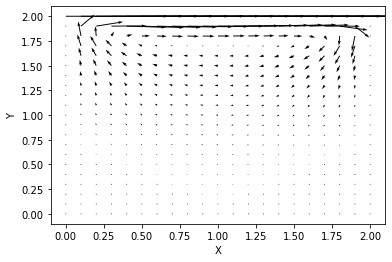
※図のサイズは特に指定していないので、小さいですがベクトルの表示もできました。
では、先ほどの圧力コンターと流速ベクトルを合わせて可視化してみましょう。
1 2 3 4 5 6 7 8 9 10 11 12 13 | #figオブジェクトで図の枠を用意 fig = plt.figure(figsize=(11,7), dpi=100) plt.contourf(X, Y, p, alpha=0.5, cmap=cm.viridis) plt.colorbar() #圧力の等高線を描く plt.contour(X, Y, p, cmap=cm.viridis) #流速ベクトルを表示 plt.quiver(X[::2, ::2], Y[::2, ::2], u[::2, ::2], v[::2, ::2]) plt.xlabel('X') plt.ylabel('Y'); |
【結果】
なんか、流体の数値計算をやったって気になれますね(^^)/
４．流線を見る
次には、流線も表示してみましょう。
1 2 3 4 5 | #流線 plt.streamplot(X, Y, u, v) plt.xlabel('X') plt.ylabel('Y') |
【結果】
※図のサイズは特に指定していないので、小さいですがベクトルの表示もできました。
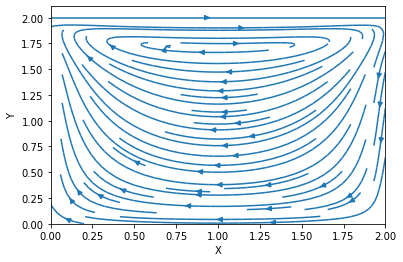
渦巻いているなーって感じれますね！
では、先ほどの圧力コンターと流線を合わせて可視化してみましょう。
1 2 3 4 5 6 7 8 9 10 11 | #figオブジェクトで図の枠を用意 fig = plt.figure(figsize=(11,7), dpi=100) plt.contourf(X, Y, p, alpha=0.5, cmap=cm.viridis) plt.colorbar() #流線 plt.streamplot(X, Y, u, v) plt.xlabel('X') plt.ylabel('Y') |
【結果】
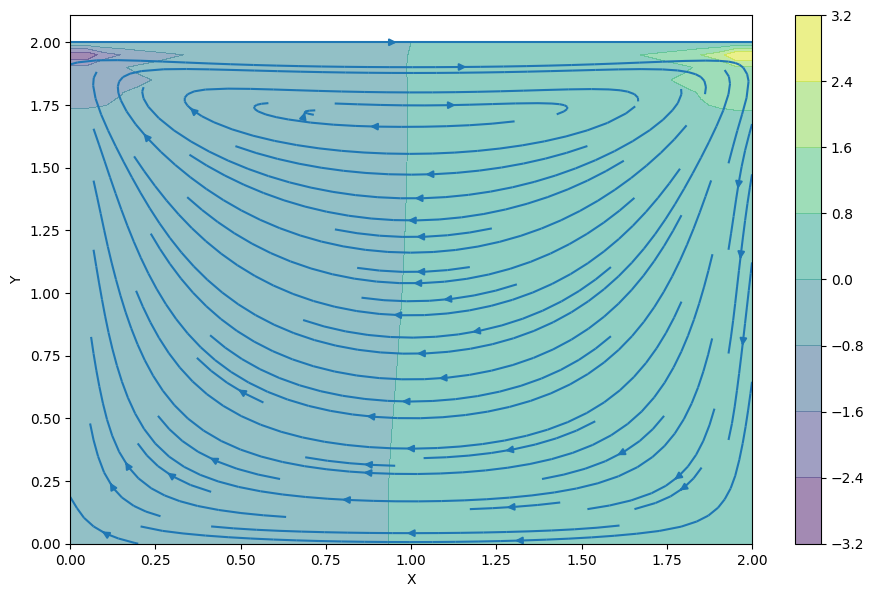
できました(^^)/
カマキリ
流体解析は楽しいです(^^)/
まとめ
今回は、2次元のナビエストークス方程式を解いてキャビティ流れをPythonで実装してみました。
過去の今回の内容に至るまでの全ての記事は、下記にまとめていますので復習ながら学習してください_(._.)_
あわせて読みたい
あとは、境界条件や空間領域などの設定を変更しながら流体の数値計算を楽しんでもらえればと思います。
※ただ、今回紹介したのは流体の数値計算のほんの一部の解き方だけです。
取り扱う流体現象や方程式によっては十分な精度がでなかったり、安定的に解いてくれなかったりします。
流体の数値計算を行う際は、以下の内容をきちんと学んでおく必要があります。
- プログラミング言語（Pythonなど）
- 流体力学
- 数値流体
- 数値計算
以下に、書籍の紹介をしておきます。
おすすめの書籍紹介
ネット上には無料で多くのことが学べるのですが、ネット情報だけだと情報が偏ったりします。
やっぱり書籍を手に取って体系だって学んだ方が良い場合も多いです。
初心者でもので体系だって学ぶことができる、且つあまり難しすぎない書籍をここで紹介しておきます。
Pythonの完全初心者は書籍で学ぶとよい
Python自体が不安だという方は、こちらの書籍から勉強しても良いかも知れません。
☟こちらの本がPython初心者が挫折することなく勉強できる本です。
（本記事のようのPython使用環境と異なりますが、とてもわかりやすいので全く問題ありません）
僕自身もこの書籍ではじめは勉強しました。
小難しい余計なことが書いていないし、年末の一週間くらいで読むことができたので、初心者の方にはとてもお勧めです。
流体の勉強をしたい方
流体の数値計算以前に、流体力学を勉強しないと！！って思っている方は以下の参考書からはじめてみるのが良いと思います。
工学よりに書かれていて実用的な内容も触れながら、流体の理論的な内容も易しく書かれていますので大学１年生で偏微分を学んだ方にとってはちょうどよい参考書です。
数値流体の書籍
本記事で紹介している数値計算手法は、多くの数値解法のごく一部です。
特に、非線形方程式で記述できる流体現象のようなものは注意深く数値解法を選択しなくてはいけません。
以下の書籍は、値段が高いですが有限体積法をメインに数値解法がとても詳しく解説されています。
数値計算の書籍
今回紹介したポアソン方程式は「ヤコビ法」と呼ばれる反復計算を行っていますが、その他の有名な数値的解法のをいくつか挙げておきます。
- ガウス消去法（直接法）
- ガウス・ジョルダン法（直接法）
- ヤコビ法（反復法）
- ガウス・ザイデル法（反復法）
- SOR法（反復法）
などがあります。
詳しく勉強したい方は、以下の参考書がとてもわかりやすいです。
数値計算の闇について詳しく知りたい方は、☟こちらの参考書も合わせてお読みください。
Follow @t_kun_kamakiri 
ナビエストークス式を勉強中です．当ブログ 大変レベルが高いですが，学びがいがあります．これからもよろしくおねがいします．
ありがとうございます。
お気づきの点ありましたらお気軽にご連絡いただけると幸いです。
よろしくお願いいたします。
コメント失礼します。NS方程式を二次元化した後３）をyで偏微分と書いてあるのですが、xではないでしょうか？意味はわかったのですが疑問に思いました。
ご指摘ありがとうございます。
xの偏微分の記述の間違いでした。その後も「(4)をyで偏微分」が正しいので修正しました。
コメントいただきありがとうございます。
コードをまねて作ってみたのですがうまくいかず、元のgithubの内容と比べてみたのですが、bの値の更新式からdtに関する項が抜けているようです。
bの更新式にdtの項を足すことで正しく計算されるようにはなりました。
しかし元のgithubの内容では、離散化前にはなかったdtに関する項が離散化後に出現しており、どのように離散化が行われたのか理解できません。
微積に無学なもので見当違いかもしれませんが、もしわかりましたら教えていただけますか。
コメントいただきありがとうございます。
途中式を書いて修正しました。
非圧縮条件の∂u/∂x +∂v/∂y = 0の条件を使うことでこれらの項を消すことができると考え、ご指摘のΔtの項を消していましたが、数値計算の誤差上残しておかないと正しく計算されないということがわかったので、Δtの項が残っているのが正しいです。
確かにgithubで離散化する前にΔtの項を消しているのに、離散化ではΔtの項を残しているのはわかりにくいと思ったので、私の記事では離散化前のΔtの式も書いておきました。
よろしくお願いいたします。