こんにちは(@t_kun_kamakiri)(^^)/
前回では「行列式の定義に従って3次と4次の正方行列の行列式」の計算方法についての内容をまとめました。
行列式の定義に従って計算するとかなり大変だったと思います。
今回は行列式計算を余因子展開を使って求める方法を紹介します。
4次以上の正方行列の行列式もわりと簡単に計算できます。
- 余因子展開
- 3次の正方行列を余因子展開で求める
- 4次の正方行列を余因子展開で求める(具体的な問題)
※4次以上の正方行列に対する行列式の計算方法は次回の記事で解説を行います。
これから線形代数を学ぶ学生や社会人のために「役に立つ内容にしたい」という思いで記事を書いていこうと考えています。
- 行列をはじめて習う高校生・大学生
- 仕事で行列を使うけど忘れてしまった社会人
この記事を読むと3次正方行列が簡単に求めることができるようになります(^^)/
余因子展開
まずは3次正方行列の行列式の計算の結果を見てみます。
行列式の定義を以下に書いておきます。
$3$行$3$列の正方行列Aについて、行列式を以下のように定義する。
|A|&=\sum sgn\, (\sigma) \cdot a_{1\sigma_{1}}a_{2\sigma_{2}}a_{3\sigma_{3}}
\end{align*}
このように定義できます。
$\sigma=\begin{pmatrix}
1 &2 &3 \\
i_{1} &i_{2} &i_{3}
\end{pmatrix}\\$
3次正方行列$A=\begin{pmatrix}
a_{11} &a_{12} & a_{13} \\
a_{21} &a_{22} & a_{23} \\
a_{31} &a_{32} & a_{33}
\end{pmatrix}\\$の行列式を行列式の定義に従って計算すると、
|A|&=\sum sgn\, (\sigma)\cdot a_{1\sigma_{1}}a_{2\sigma_{2}}a_{3\sigma_{3}}\\
&=\underset{1}{sgn\,\begin{pmatrix}
1 &2 &3 \\
1 &2 &3\end{pmatrix}}a_{11}a_{22}a_{33}+\underset{-1}{sgn\,\begin{pmatrix}
1 &2 &3 \\
1 &3 &2\end{pmatrix}}a_{11}a_{23}a_{32}\\
&+\underset{-1}{sgn\,\begin{pmatrix}
1 &2 &3 \\
2 &1 &3\end{pmatrix}}a_{12}a_{21}a_{33}+\underset{1}{sgn\,\begin{pmatrix}
1 &2 &3 \\
2 &3 &1\end{pmatrix}}a_{12}a_{23}a_{31}\\
&+\underset{-1}{sgn\,\begin{pmatrix}
1 &2 &3 \\
3 &2 &1\end{pmatrix}}a_{13}a_{22}a_{31}+\underset{1}{sgn\,\begin{pmatrix}
1 &2 &3 \\
3 &1 &2\end{pmatrix}}a_{13}a_{21}a_{32}\\
\\
&=a_{11} a_{22} a_{33}+a_{12} a_{23}a_{31}+a_{13}a_{32}a_{21}\\
&-a_{13}a_{22} a_{31}-a_{11}a_{32} a_{23} -a_{13}a_{21}a_{33}\\
&=a_{11}(-1)^{1+1}( a_{22} a_{33}- a_{32} a_{23} ) \\
&+a_{12}(-1)^{1+2}( a_{21} a_{33}- a_{23} a_{31} )\\
&+a_{13}(-1)^{1+3}( a_{21} a_{32}- a_{22} a_{33} )\\
\\
&行列式を使ってまとめる\\
\\
&=a_{11}(-1)^{1+1}\begin{vmatrix}
a_{22} & a_{23} \\
a_{32}& a_{33}\end{vmatrix}\\
&+a_{11}(-1)^{1+1}\begin{vmatrix}
a_{21} & a_{23}\\
a_{31}& a_{33}\end{vmatrix}\\
&+a_{11}(-1)^{1+1}\begin{vmatrix}
a_{21} & a_{22} \\
a_{31}& a_{33}\end{vmatrix}\tag{1}
\end{align*}
このようにまとめることができます。
どうなっているのかを以下で解説します。
余因子の作り方
まず余因子をどのように作っているかを見てみます。
例えば「1行2列の余因子を$\tilde{a}_{12}$」と書きます。


$m$行$n$列での余因子は、
- $(-1)^{m+n}$をかける
- $m$行と$n$列を除いた行列式をかける
よって1行2列の余因子は、
\tilde{a}_{12}=(-1)^{1+2}\begin{vmatrix}
a_{21} &a_{23} \\
a_{31} &a_{33} \end{vmatrix}\tag{2}
\end{align*}
となります。
余因子で展開
余因子でのポイントを押さえながら1行目について「1列目、2列目、3列目」と列に対して繰り返して行って和をとります。
$m$行$n$列での余因子は、
- $(-1)^{m+n}$をかける
- $m$行と$n$列を除いた行列式をかける
- 列で和をとる
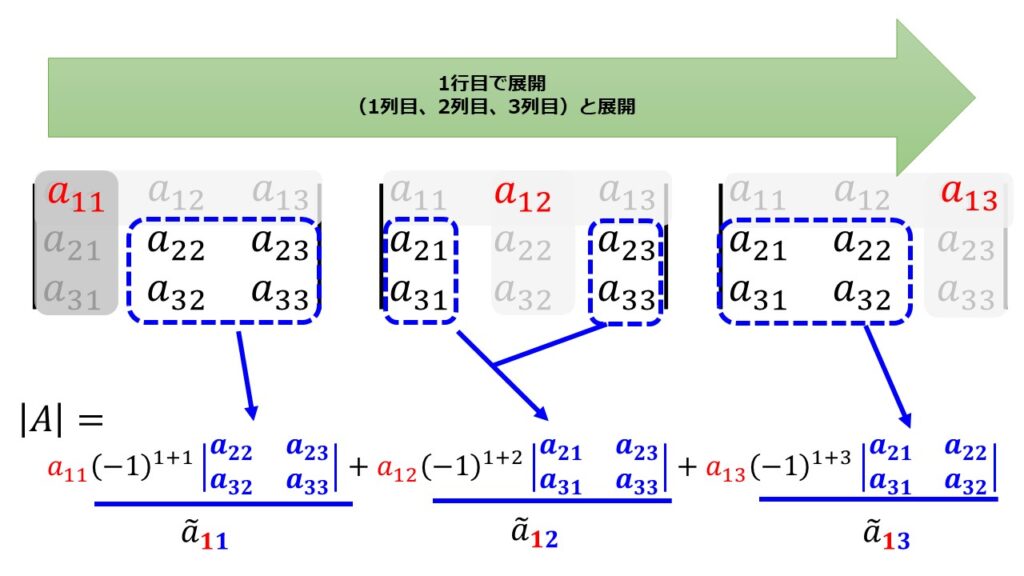

|A|&=a_{11}(-1)^{1+1}\begin{vmatrix}
a_{22} & a_{23} \\
a_{32}& a_{33}\end{vmatrix}\\
&+a_{12}(-1)^{1+2}\begin{vmatrix}
a_{21} & a_{23}\\
a_{31}& a_{33}\end{vmatrix}\\
&+a_{13}(-1)^{1+3}\begin{vmatrix}
a_{21} & a_{22} \\
a_{31}& a_{33}\end{vmatrix}\\
&=a_{11}\tilde{a}_{11}+a_{12}\tilde{a}_{12}+a_{13}\tilde{a}_{13}\tag{3}
\end{align*}
と整理できるわけです。
- 1行に目ついて展開しているので添え字の1つ目は変わっていません。
- 列で和をとっているので添え字2つ目の数字が変わっています。
以上の2点を踏まえると、
|A|&\underset{1行目で展開}{=}a_{11}\tilde{a}_{11}+a_{12}\tilde{a}_{12}+a_{13}\tilde{a}_{13}\\
&\underset{2つ目の添え字で\\和をとる}{=}\sum^{3}_{j=1}a_{1j}\tilde{a}_{1j}\tag{4}
\end{align*}
余因子展開の証明
なぜ行列式が余因子展開のように展開ができるのか?
気になりますよね。
|A|&\underset{1行目で展開}{=}a_{11}\tilde{a}_{11}+a_{12}\tilde{a}_{12}+a_{13}\tilde{a}_{13}\\
&\underset{2つ目の添え字で\\和をとる}{=}\sum^{3}_{j=1}a_{1j}\tilde{a}_{1j}\tag{4}
\end{align*}
では、さっそく証明をします。
|A|&=\begin{vmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21}& a_{22} & a_{23}\\
a_{31} & a_{32}& a_{33}\end{vmatrix}\\
&=\begin{vmatrix}
a_{11} & a_{12} & a_{13} \\
0& a_{22} & a_{23}\\
0 & a_{32}& a_{33}\end{vmatrix}
+\begin{vmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21}& 0 & a_{23}\\
a_{31} & 0& a_{33}\end{vmatrix}
+\begin{vmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21}& a_{22} & 0\\
a_{31} & a_{32}& 0\end{vmatrix}
\end{align*}
まずこのように分解ができますね。
そして、「2項目の2列目」と「3項目の3列目」を左に入れ替えていきます。
2項目の2列目の入れ替え
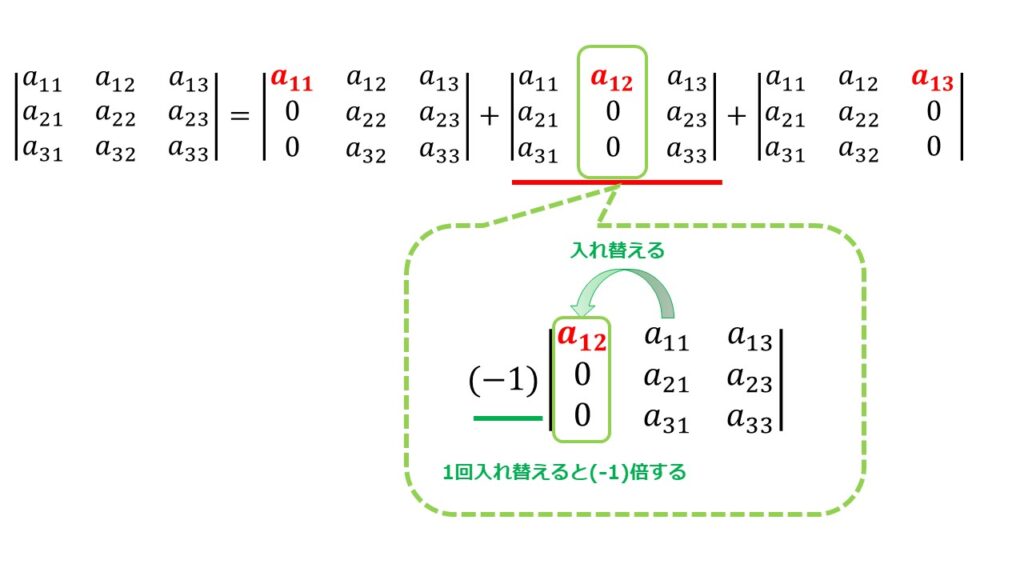

3項目の3列目の入れ替え
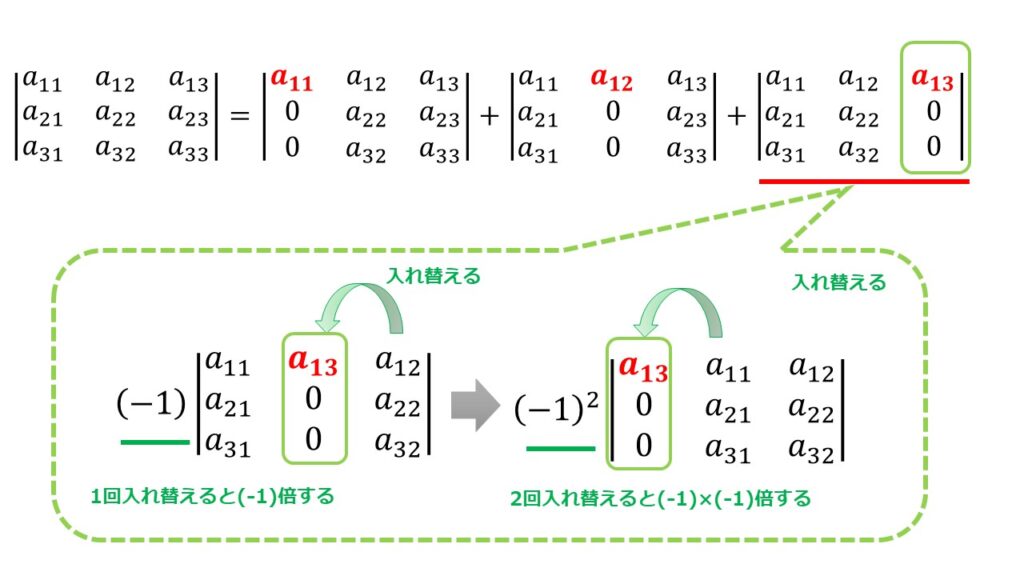

※列を入れ替えた時に入れ替えた数だけ(-1)倍をすることを忘れずに!
そしてもう少し整理すると、0がある列に関しては以下のようにできます。


以上を使って、
|A|&=a_{11}(-1)^{0}\begin{vmatrix}
a_{22} & a_{23}\\
a_{32}& a_{33}\end{vmatrix}\\
&+a_{12}(-1)^{1}\begin{vmatrix}
a_{21}& a_{23}\\
a_{31} & a_{33}\end{vmatrix}\\
&+a_{13}(-1)^{2}\begin{vmatrix}
a_{21}& a_{22} \\
a_{31} & a_{32}\end{vmatrix}\tag{5}
\end{align*}
となります。
(5)の(-1)の指数部分はどの行列を起点に展開してかをわかるように以下のようにしても同じですね。
|A|&=a_{11}(-1)^{1+1}\begin{vmatrix}
a_{22} & a_{23}\\
a_{32}& a_{33}\end{vmatrix}\\
&+a_{12}(-1)^{1+2}\begin{vmatrix}
a_{21}& a_{23}\\
a_{31} & a_{33}\end{vmatrix}\\
&+a_{13}(-1)^{1+3}\begin{vmatrix}
a_{21}& a_{22} \\
a_{31} & a_{32}\end{vmatrix}\\
&=a_{11}\tilde{a}_{11}+a_{12}\tilde{a}_{12}+a_{13}\tilde{a}_{13}
\end{align*}
※$(-1)^{2}$をかけました。
このようにまとまるわけですね。
ここで証明の流れをよく見ると別に1行目に対して展開を行いましたが、2行目や3行目に対しても同様の展開ができることがわかりますし、1列目、2列目、3列目に対しても同様ン時の展開ができることがわかりますね。
余因子展開(行で展開)
余因子展開について先ほどは1行目について展開を行いましたが、実はどの行を起点にして展開をしても同じ結果になります。
と整理できるわけです。
|A|&\underset{i行目で展開}{=}a_{i1}\tilde{a}_{i1}+a_{i2}\tilde{a}_{i2}+a_{i3}\tilde{a}_{i3}\\
&\underset{2つ目の添え字で\\和をとる}{=}\sum^{3}_{j=1}a_{ij}\tilde{a}_{ij}\tag{6}
\end{align*}
- $i$行に目ついて展開しているので添え字の1つ目は変わっていません。
- 行で和をとっているので添え字2つ目の数字が変わっています。
この2点が重要です。
これを第$i$行に関する行列式の展開といいます。
余因子展開(列で展開)
余因子展開について、行についてだけではなくどの列を起点にして展開をしても同じ結果になります。
と整理できるわけです。
|A|&\underset{j列目で展開}{=}a_{1j}\tilde{a}_{1j}+a_{2j}\tilde{a}_{2j}+a_{3j}\tilde{a}_{3j}\\
&\underset{1つ目の添え字で\\和をとる}{=}\sum^{3}_{i=1}a_{ij}\tilde{a}_{ij}\tag{7}
\end{align*}
- $j$列に目ついて展開しているので添え字の2つ目は変わっていません。
- 列で和をとっているので添え字1つ目の数字が変わっています。
この2点が重要です。
これを第$j$列に関する行列式の展開といいます。
4次正方行列の行列式の計算(余因子展開を使う)
では、余因子展開を理解したところでさっそく4次の正方行列の行列式を具体的に計算してみましょう。
今回は1列目で展開をしてみます。
問題
|A|&=\begin{vmatrix}
3 & -2 & 5 & 1 \\
1 & 3 & 2 & 5 \\
2 & -5 & -1 & 4 \\
-3 & 2 & 3 & 2 \end{vmatrix}\\
&=3(-1)^{1+1}\begin{vmatrix}
3 & 2 & 5 \\
-5 & -1 & 4 \\
2 & 3 & 2 \end{vmatrix}+1(-1)^{2+1}\begin{vmatrix}
-2 & 5 & 1 \\
-5 & -1 & 4 \\
2 & 3 & 2 \end{vmatrix}\\
&+2(-1)^{3+1}\begin{vmatrix}
-2 & 5 & 1 \\
3 & 2 & 5 \\
2 & 3 & 2 \end{vmatrix}-3(-1)^{4+1}\begin{vmatrix}
-2 & 5 & 1 \\
3 & 2 & 5 \\
-5 & -1 & 4 \end{vmatrix}\\
\\
&\underset{サラスの公式}{=}3\times(-71)-105+2\times(47)-3\times(-1)\times(-204)\\
&=-836
\end{align*}
最後は3次行列式になればサラスの公式を使えば簡単に行列式が求まります。
4次正方行列の行列式を余因子展開で求めると割と簡単でしたね。
まとめ
今回は、
についての内容をまとめ、4次正方行列の行列式を具体的に計算しました。
$m$行$n$列での余因子は、
- $(-1)^{m+n}$をかける
- $m$行と$n$列を除いた行列式をかける
余因子の作り方はこちらの絵をよく覚えておくことですね。
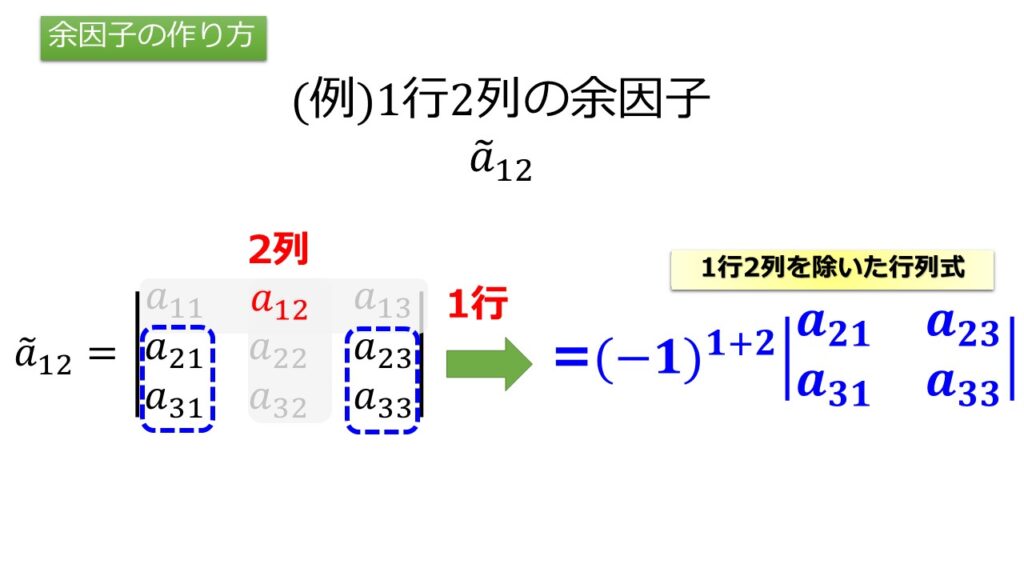

余因子展開の展開の仕方は「行に関して」と「列に関して」に対して行うことができます。
|A|&\underset{i行目で展開}{=}a_{i1}\tilde{a}_{i1}+a_{i2}\tilde{a}_{i2}+a_{i3}\tilde{a}_{i3}\\
&\underset{2つ目の添え字で\\和をとる}{=}\sum^{3}_{j=1}a_{ij}\tilde{a}_{ij}\tag{6}
\end{align*}
- $i$行に目ついて展開しているので添え字の1つ目は変わっていません。
- 行で和をとっているので添え字2つ目の数字が変わっています。
この2点が重要です。
これを第$i$行に関する行列式の展開といいます。
|A|&\underset{j列目で展開}{=}a_{1j}\tilde{a}_{1j}+a_{2j}\tilde{a}_{2j}+a_{3j}\tilde{a}_{3j}\\
&\underset{1つ目の添え字で\\和をとる}{=}\sum^{3}_{i=1}a_{ij}\tilde{a}_{ij}\tag{7}
\end{align*}
- $j$列に目ついて展開しているので添え字の2つ目は変わっていません。
- 列で和をとっているので添え字1つ目の数字が変わっています。
この2点が重要です。
参考にする参考書はこれ
当ブログでは、以下の2つの参考書を読みながらよく使う内容をかいつまんで、一通り勉強すればついていけるような内容を目指していこうと思います。
大事なところをかいつまんで、「これはよく使うよな。これを理解するためには補足で説明をする」という調子で進めていきます(^^)/