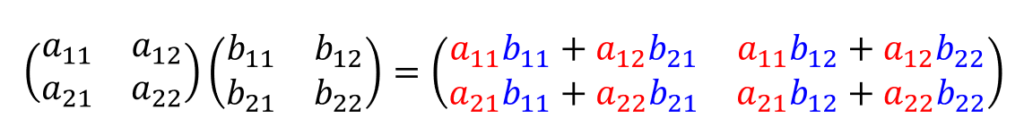こんにちは(@t_kun_kamakiri)(^^)/
前回は固有値と固有ベクトルの解説を行いました。
今回は固有値と固有ベクトルのお話の続きで対角行列の解説を行います。
固有値方程式から求まる固有値と固有ベクトルを知ることで対角行列や基底変換など面白い内容が待っています(^^)
固有値方程式から求めた固有ベクトルを使って対角行列を作る
これから線形代数を学ぶ学生や社会人のために「役に立つ内容にしたい」という思いで記事を書いていこうと考えています。
- 行列をはじめて習う高校生・大学生
- 仕事で行列を使うけど忘れてしまった社会人
この記事の内容をマスターして線形独立と線形従属を理解しましょう(^^)
復習：固有値と固有ベクトル
前回の復習を簡単にしておきます。
固有値方程式
A\boldsymbol{x}=\alpha \boldsymbol{x}
\end{align*}
において$\boldsymbol{x}$を固有ベクトル、$\alpha$を固有値といいます。
固有値は$|A-\alpha E|=0$より求めることができます。
対角行列とは
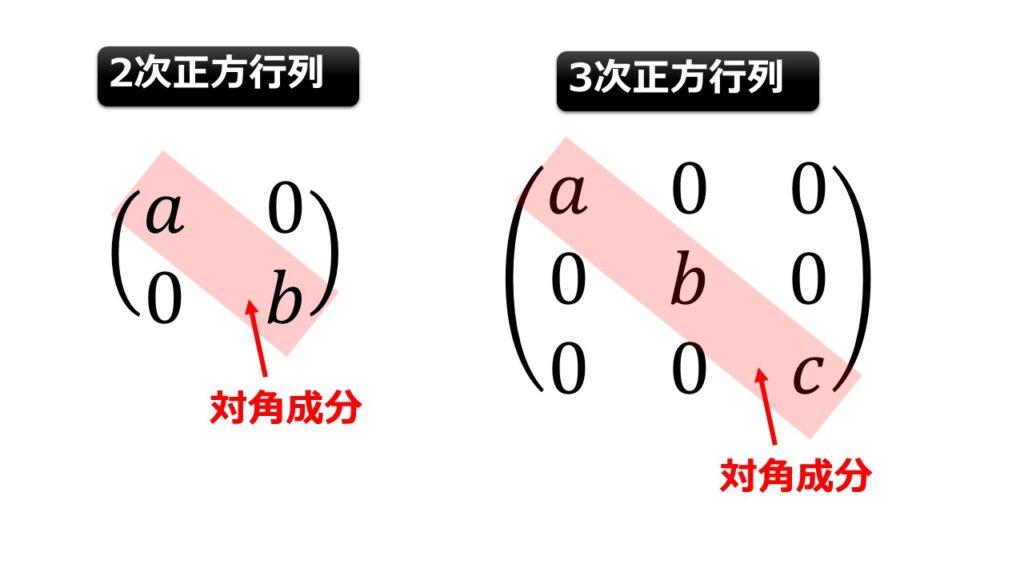
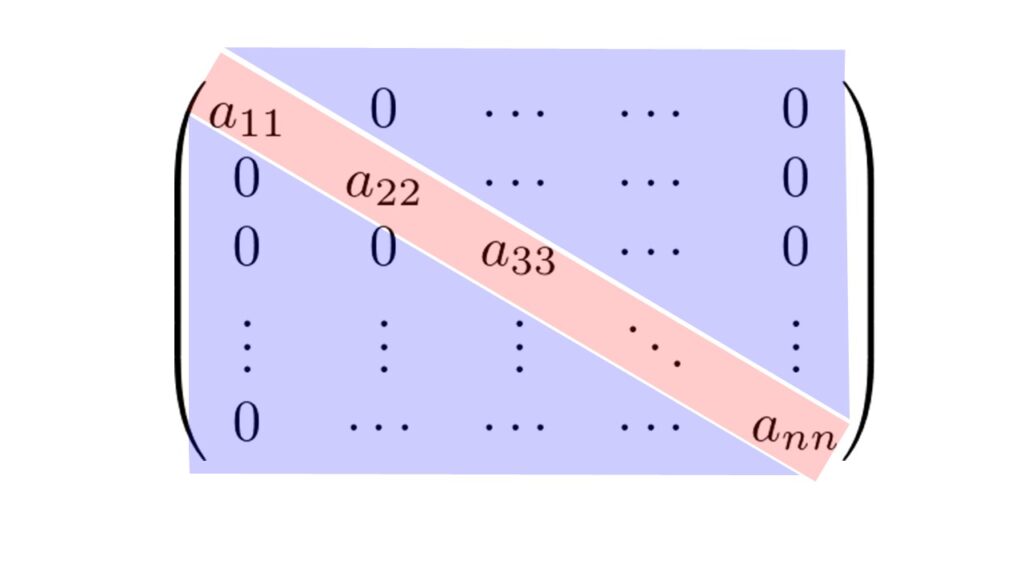
対角行列とは正方行列に対して対角成分以外は0である行列のことです。
2次正方行列と3次正方行列を例にとると以下のような行列です。
行列の成分を$i$行$j$列の成分を$a_{ij}$とすると、$i \neq jのとき$a_{ij}=0である行列が対角行列といいます。
\begin{pmatrix}
a_{11} & 0 & \cdots & \cdots & 0 \\
0 & a_{22} & \cdots & \cdots & 0 \\
0 & 0 & a_{33} & \cdots & 0\\
\vdots & \vdots & \vdots & \ddots &\vdots \\
0 & \cdots & \cdots & \cdots&a_{nn} \\
\end{pmatrix}
\end{align*}
左上から右下にかけて数字が入っていて、それ以外の成分が全て0になっている行列なんだなと思ってもらえれば良いです。
このような対角成分以外は0である対角行列を固有値方程式から求めた固有値と固有ベクトルを使って作ることができます。
対角行列を作ったら何が嬉しいのかは次回の記事で解説することにして、ここでは対角行列を作る計算の手続きを理解しておくことを優先にします。
2次正方行列の固有ベクトルから対角行列を作る
一般的な$n$次正方行列の解説を行う前に、前回解説に使った2次正方行列$A=\begin{pmatrix}
4 & -2 \\
1 & 1 \\
\end{pmatrix}$を例に対角行列を作る手順を解説します。
ここまでは前回の記事で求めました。
これを以下のように固有値方程式に代入して書き並べてみましょう。
A\boldsymbol{x}_{1}=\alpha_{1} \boldsymbol{x}_{1}\tag{1}
\end{align*}
A\boldsymbol{x}_{2}=\alpha_{2} \boldsymbol{x}_{2}\tag{2}
\end{align*}
これを行列を使ってひとつにまとめることができます。
A\begin{pmatrix}
\boldsymbol{x}_{1}& \boldsymbol{x}_{2}
\end{pmatrix}=
\begin{pmatrix}
\boldsymbol{x}_{1}& \boldsymbol{x}_{2}
\end{pmatrix}
\begin{pmatrix}
\alpha_{1} & 0\\
0 & \alpha_{2}
\end{pmatrix}
\tag{3}\end{align*}
右辺に対角行列ができていますね。
これは以下のような計算を行えば成立していることが確認できるでしょう。
ここで$\begin{pmatrix}
\boldsymbol{x}_{1}& \boldsymbol{x}_{2}
\end{pmatrix}$に着目すると、ベクトルの成分を用いて書くと以下になっています。
\begin{pmatrix}
\boldsymbol{x}_{1}& \boldsymbol{x}_{2}
\end{pmatrix}=\begin{pmatrix}
1& 2\\
1& 1\\
\end{pmatrix}\tag{4}\end{align*}
これを$P=\begin{pmatrix}\boldsymbol{x}_{1}& \boldsymbol{x}_{2}
\end{pmatrix}$とおくことにします。
そうすると、(3)は以下のようになります。
AP=P\begin{pmatrix}
\alpha_{1} & 0\\
0 & \alpha_{2}
\end{pmatrix}
\end{align*}
右辺に対角行列ができているので両辺に$P$の逆行列$P^{-1}$を左から掛けてやれば右辺は対角行列のみになりますね。
ただ、行列$P$が逆行列を持つかどうかは掛ける前に注意しなくてはいけません。
しかし、行列$P$は固有ベクトル$\boldsymbol{x}_{1}$,$\boldsymbol{x}_{2}$でできている行列であり、異なる固有値に対する固有ベクトルである$\boldsymbol{x}_{1}$と$\boldsymbol{x}_{2}$は線形独立な関係にあるので必ず逆行列を持ちます。
P^{-1}AP=P^{-1}P\begin{pmatrix}
\alpha_{1} & 0\\
0 & \alpha_{2}
\end{pmatrix}
\end{align*}
$P^{-1}P=E$(単位行列)なので右辺は$\begin{pmatrix}
\alpha_{1} & 0\\
0 & \alpha_{2}
\end{pmatrix}$のみになります。
よって、
P^{-1}AP=\begin{pmatrix}
\alpha_{1} & 0\\
0 & \alpha_{2}
\end{pmatrix}\tag{5}
\end{align*}
のように固有ベクトルを使って固有値を対角成分に持つ対角行列を作ることができました。
対角行列の何が嬉しいのか？
対角成分以外を0にしていったい何が嬉しいのかと思うかもしれませんね。
対角行列の嬉しさは行列の掛け算において計算がやりやすくなるメリットがあります。
行列の掛け算というのはめちゃくちゃ面倒なんでしたね。
計算量の削減
たかだか2行2列の行列の掛け算でも以下のように2（1成分）×2（行方向）×2（列方向）=8回の掛け算を行うことになります。
これが対角行列の掛け算だと4回の掛け算で済むわけです。
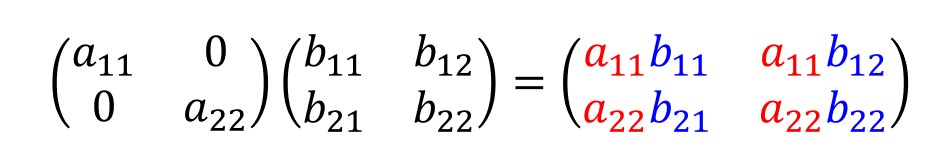
行列のべき乗の計算が簡単
例えば$A=\begin{pmatrix}
4 & -2 \\
1 & 1 \\
\end{pmatrix}$の行列を$A^2,A^3,\cdots,A^{n}$のように計算していった結果はどうなるかは計算してみないとわからないです。
ただ、対角行列$A=\begin{pmatrix}
2 & 0 \\
0 & 3 \\
\end{pmatrix}$を$A^2,A^3,\cdots,A^{n}$のように計算していった結果はすぐにわかります。
- $A^2=\begin{pmatrix}
2^2 & 0 \\
0 & 3^2 \\
\end{pmatrix}$ - $A^3=\begin{pmatrix}
2^3 & 0 \\
0 & 3^3 \\
\end{pmatrix}$ - $\vdots$
- $A^n=\begin{pmatrix}
2^n & 0 \\
0 & 3^n \\
\end{pmatrix}$
対角成分を$n$乗するだけで求めることができます。
まとめ
本記事では固有ベクトル$\boldsymbol{x}_{1}$,$\boldsymbol{x}_{2}$を基底に取るような線形空間を考えると行列$A$が対角行列になることを示しました。
次回の記事は基底変換について解説を行います。
基底を変えることで対角行列を作ることができ、本記事の最後に示したように対角行列になれば行列の計算が簡単になるのでとても便利ですね。
今までは線形空間は考えやすくするために基底を$\boldsymbol{e}_{1}=\begin{pmatrix}
1\\
0\\
\end{pmatrix}$と$\boldsymbol{e}_{2}=\begin{pmatrix}
0\\
1\\
\end{pmatrix}$を考えていました。
このとき行列$A=
\begin{pmatrix}
4 & -2 \\
1 & 1 \\
\end{pmatrix}$という変換行列は全ての行と列に数字が入っているので$A\boldsymbol{x}$を計算しようものなら結果が$A\boldsymbol{x}=
\begin{pmatrix}
4 & -2 \\
1 & 1 \\
\end{pmatrix}\begin{pmatrix}
x_1 \\
x_2 \\
\end{pmatrix}=\begin{pmatrix}
4x_1-2x_2 \\
x_1+x_2 \\
\end{pmatrix}$と行列計算の中で4回掛け算を行うことになりますよね。$A$が2行2列の計算ならそれほど手間ではありませんが、100行100列ともなると$A\boldsymbol{x}$のひとつの要素で100回の掛け算を行うので、それが100行あると100×100回掛け算をすることになります。
さらに$AB$のような100行100列どうしの行列の積だと、一つの要素で100個の掛け算、さらに$AB$の行列は100行100列ですから、100×100×100回掛け算をすることになります。考えただけでも途方もないですね。
これは空間を作るための基底を別のものに変えて、その基底での$A$に対応する行列が$A^{\prime}=\begin{pmatrix}
\alpha_{1} & 0\\
0 & \alpha_{2} \\
\end{pmatrix}$のような対角成分にのみ値を持つ対角行列になってくれたらなんて嬉しいことでしょう。
$A^{\prime}=\begin{pmatrix}
\alpha_{1} & 0\\
0 & \alpha_{2} \\
\end{pmatrix}\begin{pmatrix}
x_{1}\\
x_{2}
\end{pmatrix}=\begin{pmatrix}
\alpha_{1}x_{1}\\
\alpha_{2}x_{2}
\end{pmatrix}$のように簡単に計算できますよね。
基底を変えて$A$に対応する行列が対角行列になってくれたら、例えば100行100列の行列計算でもそのほとんどが0になるので100回の掛け算の計算で済みます。
そして計算し終わったらもとの基底に戻す変換を行えばよいですよね。
次回は「対角行列と基底変換」の話をします。
今回使った固有値・固有ベクトルをがっつり使うので本記事の内容をしっかりと押さえておきましょう。
参考にする参考書はこれ
当ブログでは、以下の3つの参考書を読みながらよく使う内容をかいつまんで、一通り勉強すればついていけるような内容を目指していこうと思います。
大事なところをかいつまんで、「これはよく使うよな。これを理解するためには補足で説明をする」という調子で進めていきます(^^)/
Follow @t_kun_kamakiri 