こんにちは(@t_kun_kamakiri)。
本日は、「2次元の移流方程式」をPythonで実装するというのをやります。
前回の記事までで、「1次元の移流方程式」「1次元の拡散方程式」「1次元バーガース方程式」など1次元の偏微分方程式ばかりでしたが、今回から2次元の数値計算を行います。
次元が増えるだけで数値計算の手法は特に変わらないので、それほど難しさはないかと思います!
☟こんな感じのをアニメーションにしてみます(^^)/
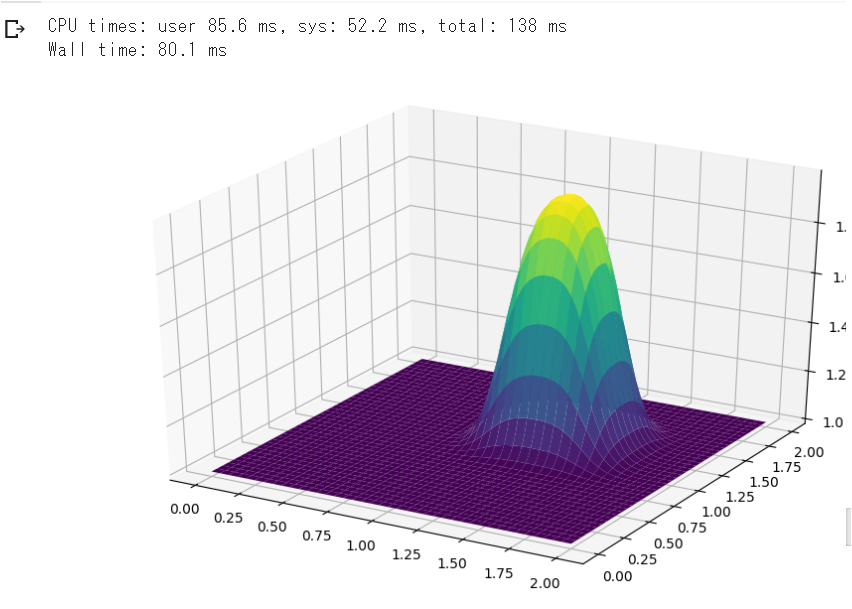
本件の基本的な内容はこちらのサイトにそってやっていきます。
この記事ではこんな人を対象にしています。
- Pythonを使い始めたけどどう使うかわからない
- 流体の数値計算をはじめて勉強する人
本記事シリーズの最終目標は、ナビエストークス方程式をPythonで実装することですが、いきなりナビエストークス方程式を実装するのは難しいので各項の意味を確認しながら進めていきたいと思います。
- 2次元の移流方程式の数値計算
- スライスとfor文の計算速度の違い
- 2次元のアニメーション作成
2次元の移流方程式の離散化
速度ベクトルを$\boldsymbol{u}=(u,v,0)$とします。
\frac{\partial \boldsymbol{u}}{\partial t}+c\nabla\cdot \boldsymbol{u} = 0
\end{align*}
\frac{\partial u}{\partial t}+c\frac{\partial u}{\partial x} + c\frac{\partial u}{\partial y} = 0\\
\frac{\partial v}{\partial t}+c\frac{\partial v}{\partial x} + c\frac{\partial v}{\partial y} = 0\tag{1}
\end{align*}
\frac{u_{i,j}^{n+1}-u_{i,j}^n}{\Delta t} + c\frac{u_{i, j}^n-u_{i-1,j}^n}{\Delta x} + c\frac{u_{i,j}^n-u_{i,j-1}^n}{\Delta y}=0\\
\frac{v_{i,j}^{n+1}-v_{i,j}^n}{\Delta t} + c\frac{v_{i, j}^n-v_{i-1,j}^n}{\Delta x} + c\frac{v_{i,j}^n-v_{i,j-1}^n}{\Delta y}=0\tag{2}
\end{align*}
u(x,y) = \begin{cases}
\begin{matrix}
2\ \text{for} & 0.5 \leq x, y \leq 1 \cr
1\ \text{for} & \text{それ以外}\end{matrix}\end{cases}
\tag{4}
\end{align*}
u = 1\ \text{for } \begin{cases}
\begin{matrix}
x = 0,\ 2 \cr
y = 0,\ 2 \end{matrix}\end{cases}\tag{5}
\end{align*}
Pythonを使って2次元移流方程式の初期状態を3次元可視化
【ポイント】
- Matpltlibのmplot3dで3次元の可視化ライブラリをインポート
- 条件設定
- 初期状態の生成
- 初期状態のプロファイルの可視化
今回3次元の可視化のために、今まで使ったことのないライブラリを使うので後ほど解説をしたいと思います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
from mpl_toolkits.mplot3d import Axes3D import numpy as np import matplotlib.pyplot as plt from matplotlib import cm #条件設定 nx = 81 ny = 81 nt = 100 c = 1 dx = 2 / (nx - 1) dy = 2 / (ny - 1) sigma = .2 dt = sigma * dx x = np.linspace(0, 2, nx) y = np.linspace(0, 2, ny) #初期状態 u = np.ones((ny, nx)) un = np.ones((ny, nx)) u[int(.5 / dy):int(1 / dy + 1),int(.5 / dx):int(1 / dx + 1)] = 2 #プロファイルの可視化 fig = plt.figure(figsize=(11, 7), dpi=100) ax = fig.gca(projection='3d') X, Y = np.meshgrid(x, y) surf = ax.plot_surface(X, Y, u[:], cmap=cm.viridis) |
【結果】
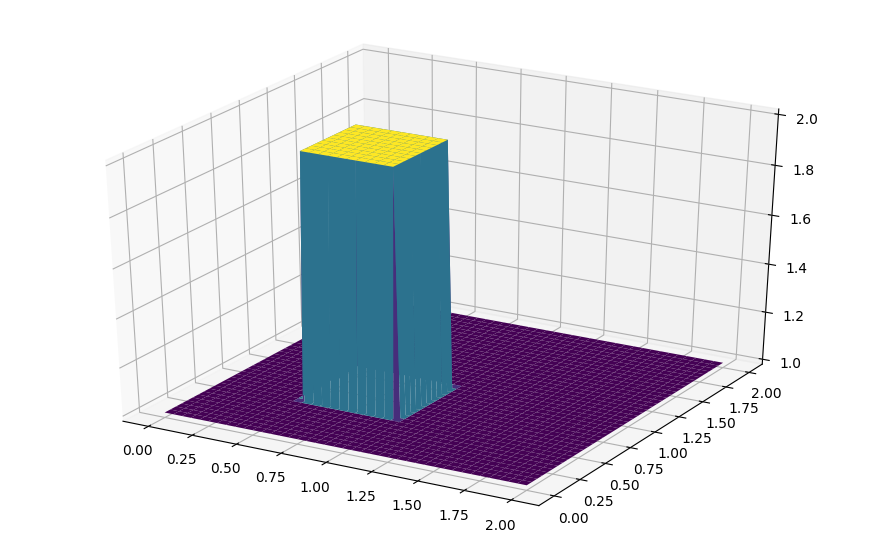


※コメントがありましたので追加しておきます。

では、今回使っている新しいライブラリについて解説を加えておきます(^^)/
Matpltlibのmplot3dで3次元の可視化ライブラリをインポート
1行目で「from mpl_toolkits.mplot3d import Axes3D」としています。
ここではちょっとした解説を加える程度にしておきますが、詳細はこちらの公式ドキュメントで使い方の解説が載っていますので是非参考にしてください。
まず、matplotlibのpyplotをインポートします。
|
1 |
import matplotlib.pyplot as plt |
その次に、「figureオブジェクト」で枠を設定します。
|
1 2 3 |
fig = plt.figure(figsize=(11, 7), dpi=100) ax = fig.gca(projection='3d') print(type(fig)) |
【結果】


このように、figure windowを作成しています。
- 「fig = pyplot.figure()」でpyplotの中のfigure()をインスタンス化しています。
- figsize:画像サイズ
- dpi:画像の解像度
- 「ax = fig.gca(projection=’3d’)」でfigをaxに割り当てています。
次に、メッシュ生成とuの分布の指定をします。
|
1 2 |
X, Y = np.meshgrid(x, y) surf = ax.plot_surface(X, Y, u[:], cmap=cm.viridis) |
【結果】



- 「X, Y = np.meshgrid(x, y) 」:X,Yのメッシュグリッドの指定をしています。
- 「ax.plot_surface(X, Y, u[:], cmap=cm.viridis)」:メッシュグリッドとuの値の分布を指定します。
2次元移流方程式をPythonで実装
では、先ほどの初期状態から「nt = 100」ステップ後のuのプロファイルを3次元可視化したいと思います。
各ステップを計算しながらステップごとに計算領域の要素を計算しないといけないためfor文を使う必要があります。
でも、前回の記事で解説したようにfor文を使ったコードは計算時間が遅いんですよね。
for文を使わずにスライスを使った計算の方が速いことは検証済みなので、スライスのありがたみを実感してもらうために、
for文とスライスの計算時間を計測して比較を行いたいと思います。
まずは、for文を使ったコードから書いてみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
%%time u = np.ones((ny, nx)) u[int(.5 / dy):int(1 / dy + 1), int(.5 / dx):int(1 / dx + 1)] = 2 for n in range(nt + 1): ##loop across number of time steps un = u.copy() row, col = u.shape for j in range(1, row): for i in range(1, col): u[j, i] = (un[j, i] - (c * dt / dx * (un[j, i] - un[j, i - 1])) - (c * dt / dy * (un[j, i] - un[j - 1, i]))) u[0, :] = 1 u[-1, :] = 1 u[:, 0] = 1 u[:, -1] = 1 fig = plt.figure(figsize=(11, 7), dpi=100) ax = fig.gca(projection='3d') surf2 = ax.plot_surface(X, Y, u[:], cmap=cm.viridis) |
【結果】


だいたい計算時間は3秒くらいですかね。
では、同じことをスライスとを使ってコードを書いてみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
%%time u = np.ones((ny, nx)) u[int(.5 / dy):int(1 / dy + 1), int(.5 / dx):int(1 / dx + 1)] = 2 for n in range(nt + 1): ##loop across number of time steps un = u.copy() u[1:, 1:] = (un[1:, 1:] - (c * dt / dx * (un[1:, 1:] - un[1:, :-1])) - (c * dt / dy * (un[1:, 1:] - un[:-1, 1:]))) u[0, :] = 1 u[-1, :] = 1 u[:, 0] = 1 u[:, -1] = 1 fig = plt.figure(figsize=(11, 7), dpi=100) ax = fig.gca(projection='3d') surf2 = ax.plot_surface(X, Y, u[:], cmap=cm.viridis) |
【結果】


計算時間はだいたい「100~200ms」くらいです。
スライスを使った方が、for文を使った場合より10倍くらい計算が速いですね。
アニメーション作成
3次元の可視化はできても、静止画だとなんか面白みがないのでアニメーション作成をしたいと思います。
アニメーション作成も結構時間がかかったりするので、必要ない方はアニメーション作成しなくても良いかと思います_(._.)_
Google Colaboratoryのアニメーション作成はちょっと特殊なので調べながら作ってみました。
以前の記事では、アニメーション作成には、「matplotlib.animation.ArtistAnimation」を使いましたが今回は、「matplotlib.animation.FuncAnimation」を使います。
一応、両者の違いを完結に述べておこうと思います。
- matplotlib.animation.ArtistAnimation:グラフのオブジェクトのリストを格納することでアニメーションを作成する。
- matplotlib.animation.FuncAnimation:グラフ行進用の関数を用意して逐一更新しながらアニメーションを作成する。
全体のPythonコードは以下です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 |
import numpy as np from matplotlib import pyplot as plt from matplotlib import cm from mpl_toolkits.mplot3d import Axes3D ##library for 3d projection plots import matplotlib.animation as animation #条件設定 nx = 31 ny = 31 nt = 80 c = 1 dx = 2 / (nx - 1) dy = 2 / (ny - 1) alpha = 0.2 dt = alpha * (dx/c) x = np.linspace(0, 2, nx) y = np.linspace(0, 2, ny) x = np.linspace(0, 2, nx) y = np.linspace(0, 2, ny) #初期状態 u = np.ones((ny, nx)) un = np.ones((ny, nx)) u[int(.5 / dy):int(1 / dy + 1),int(.5 / dx):int(1 / dx + 1)] = 2 v = np.ones((ny, nx)) vn = np.ones((ny, nx)) v[int(.5 / dy):int(1 / dy + 1),int(.5 / dx):int(1 / dx + 1)] = 2 fig = plt.figure() ax = fig.gca(projection='3d') ax.set_zlim(1, 2.5) ax.set_xlabel('$x$') ax.set_ylabel('$y$') ax = fig.gca(projection='3d') X, Y = np.meshgrid(x, y) surf = ax.plot_surface(X, Y, u, rstride=1, cstride=1, cmap=cm.viridis,linewidth=0, antialiased=False) def updata(nt): un = u.copy() vn = v.copy() u[1:, 1:] = (un[1:, 1:] - (un[1:, 1:] * c * dt / dx * (un[1:, 1:] - un[1:, :-1])) - vn[1:, 1:] * c * dt / dy * (un[1:, 1:] - un[:-1, 1:])) # v[1:, 1:] = (vn[1:, 1:] - # (un[1:, 1:] * c * dt / dx * (vn[1:, 1:] - vn[1:, :-1])) - # vn[1:, 1:] * c * dt / dy * (vn[1:, 1:] - vn[:-1, 1:])) u[0, :] = 1 u[-1, :] = 1 u[:, 0] = 1 u[:, -1] = 1 # v[0, :] = 1 # v[-1, :] = 1 # v[:, 0] = 1 # v[:, -1] = 1 ax.set_title('time = '+ str(round(nt*dt,2))+ 'sec, '+ str(nt)+'step') ax.plot_surface(X, Y, u[:], rstride=1, cstride=1, cmap=cm.viridis,linewidth=0, antialiased=True) |
こちらの計算自体はすぐに終わります。
※アニメーション作成の時間短縮のために空間の分割数は「31分割」と少なめにしました。
※y方向の速度も解かないようにしています。
👆こうしないとアニメーション作成に時間がかかりすぎましてね(‘_’)
そして、こちらの記事を参考に必要な記述は何かを調べながらコードを確認して、「JupiterにMatplotlibアニメーションをインタラクティブなJavaScriptウィジェットとして埋め込む」という方法でGoogle Colaboratoryでもアニメーションができました。
|
1 2 3 |
from IPython.display import HTML ani = animation.FuncAnimation(fig, updata, interval = 100,frames = 80) HTML(ani.to_html5_video()) |
正直この方法はアニメーション作成にはめちゃくちゃ時間がかかるので微妙です(笑)
※アニメーション作成に3分くらいかかりました(笑)
なんかアニメーション作成がじゃっかん残像を残しながらというのはきになりますが、アニメーション作成はGoogle Colaboでもできました!
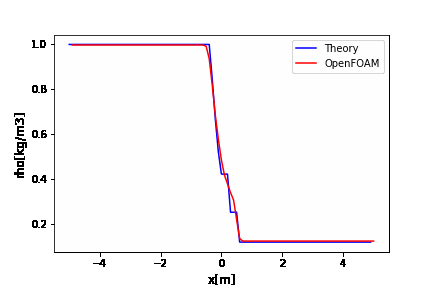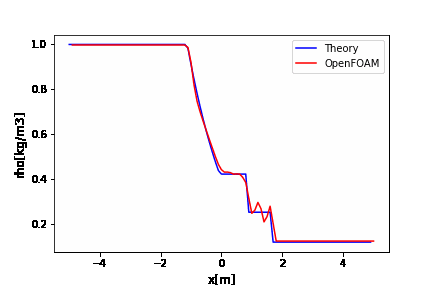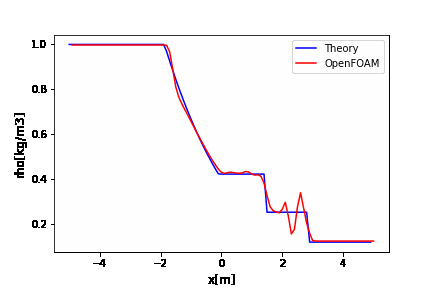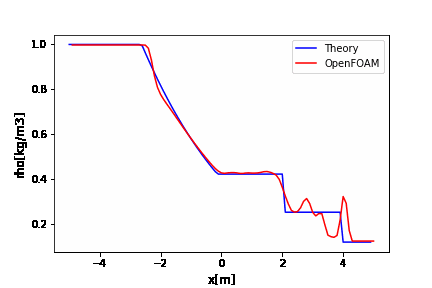
アニメーションを見る限り、移流方程式に1次精度の後退差分を使うと安定に解いてくれますが、解が拡散しながら時間発展していきますね。
移流方程式は形を変えずに速度\(c\)で伝播する方程式なのに・・・・
こういった数値粘性があるのかーって覚えておいてもらえれば、新たに記事を追加して解説を加えたいと思います。
まとめ
今回は、2次元の移流方程式をPythonで実装してアニメーション確認までしました。
- 2次元移流方程式の1次精度後退差分では数値拡散が起こる
- スライスはfor文より計算が速い
- Google Colaboアニメーション作成はちょっと面倒
Pythonの完全初心者は書籍で学ぶとよい
Python自体が不安だという方は、こちらの書籍から勉強しても良いかも知れません。
☟こちらの本がPython初心者が挫折することなく勉強できる本です。
(本記事のようのPython使用環境と異なりますが、とてもわかりやすいので全く問題ありません)
流体の勉強をしたい方
流体の数値計算以前に、流体力学を勉強しないと!!って思っている方は以下の参考書からはじめてみるのが良いと思います。
工学よりに書かれていて実用的な内容も触れながら、流体の理論的な内容も易しく書かれていますので大学1年生で偏微分を学んだ方にとってはちょうどよい参考書です。


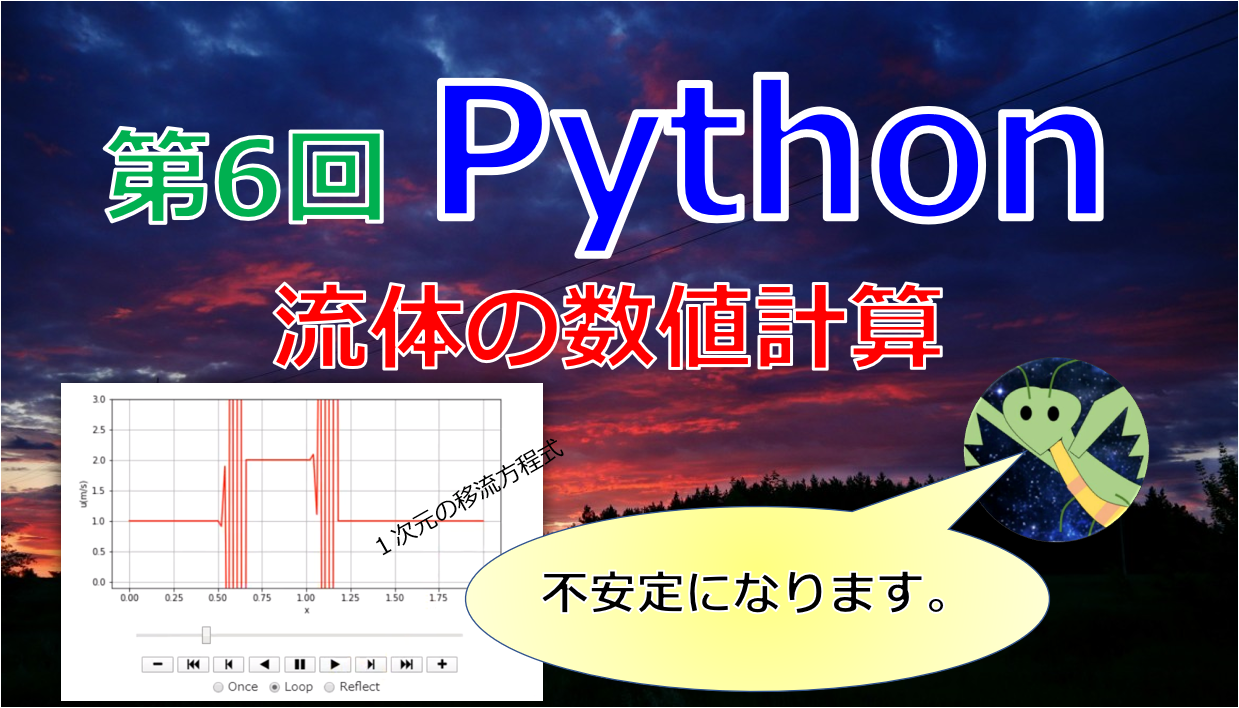




















なぜ, dtを定義するときsigmaを0.2と定義したのかを教えていただきたいです.
コメントありがとうございます。
参考にしたリンク(https://github.com/barbagroup/CFDPython/blob/master/lessons/07_Step_5.ipynb)がsigma=0.2だったからと言えばそれまでなのですが、
sigma=0.2にした理由は、cΔt/Δx≦1を満たさないと計算が不安定になるからです。
つまり、Δt≦Δx/cでないと不安定になります。
今の場合、c=1なのでΔt≦Δxとしなくては不安定で結果が振動してしまいます。
ゆえに、Δt=sigma*Δxとしてsigma=0.2にすることで、確実にΔt≦Δxとなるようにしています。
☟その原理はこちらの記事にも書いていますので、是非お読みください(..)_
https://takun-physics.net/9600/