こんにちは（@t_kun_kamakiri）(‘◇’)ゞ
本記事では、断熱自由膨張でのエントロピーを計算したいと思います。
当ブログでは以下のような構成で記事を書いていきます。
- はじめてでもわかるエントロピーの意味
- エントロピーの意味をわかりやすく解説。不可逆性と取りうる状態の場合の数。
- エントロピーは熱/温度と定義する
- エントロピー増大の法則をわかりやすく解説
- 断熱自由膨張は断熱過程でもエントロピー増大する
エントロピーを熱力学の観点からなぜ「エントロピーを乱雑さの度合い」と表現されるのかをわかりやすく解説する。
エントロピーとは何か
断熱自由膨張を考える前にエントロピーについて復習しておきましょう。
- 不可逆性を示す指標
- 分子の取りうる状態の場合の数の指標
不可逆性の話は熱力学でのエントロピーの定義から言えることです。「分子の取りうる状態の場合の数の指標」は統計学でのエントロピーの定義になるためここでは割愛します。
不可逆性についてわからない方もいると思います。エントロピーを理解するうえで不可逆性はとても重要な用語ですので是非覚えておいてください。
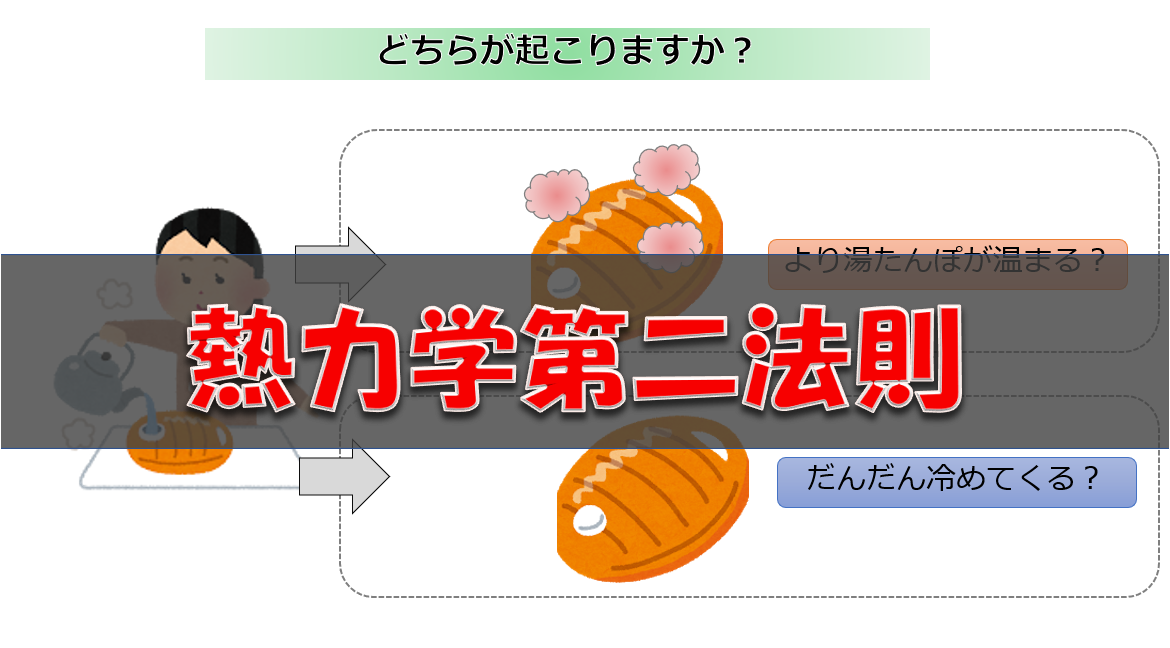
これは熱力学第二法則に関係していることです。
不可逆性とは何も手を加えずに実現することは無理ですよね。
自然に戻ることがない
これが不可逆性です。
確かに意図的に手を加えれば、割れた花瓶が元に戻すことができるしミルクも一か所に固めることができます。湯たんぽを温めれば確かに元に戻ります。
ここでいう不可逆というのには「自発的に起こる変化の方向」があって、手を加えなければ起こりえない方向の事を言っています。
自発的に変化する向きであるエントロピーを定量化
系の状態は自発的に変化する向きを定量的に評価できないか？ということを考えます。
この難しい概念を定量的に評価してくれるのがエントロピーの役割といえるでしょう。
エントロピーを以下のように定義します。
$$\Delta S = \frac{Q}{T}$$
言葉で書くと、エントロピー変化を$\Delta S$は出入りした熱量$\Delta Q$を温度$T$で割ったものと定義されます。
微分形式で書くのであれば$dS=\frac{d^{\prime}Q}{T}$と書けます。
エントロピーは$dS$と書いているのに熱量に関して$dQ$と書かずに$d^{\prime}Q$と書いているのには理由があります。
エントロピーは状態量なので$\Delta S=S_{終}-S_{始}$と始めの状態と終わりの状態の差で書くことができますが、熱量は状態量ではないので出入りした熱量はどのように熱が入ってきたかという積分値$Q=\int dQ$でしか書けないため$\Delta Q=Q_{終}-Q_{始}$のような書き方ができません。
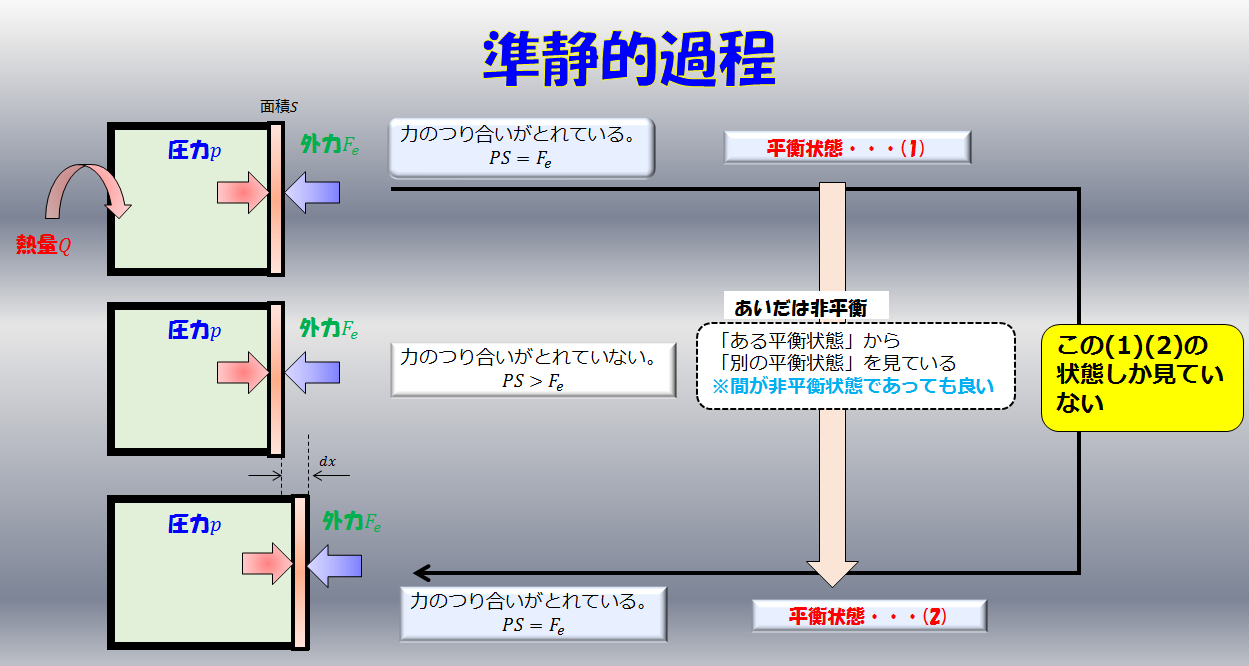
注意して欲しいのはエントロピーが$dS=\frac{d^{\prime}Q}{T}$とイコールで結んで定義できるのは熱の出入りが準静的過程の場合だけです。
準静的過程とはゆ〜っくり、ゆ〜っくり熱の出入りがある過程のことで、その過程では熱平衡状態が保たれているため熱力学的な物量が定義できます。
断熱自由膨張は途中で準静的過程ではない過程が入るため熱平衡状態ではない状態が生じます。ゆえに、断熱自由膨張の過程ではエントロピーが定義できないということです。なので、$p-V$図にもその変化の過程を図示することができません。
もしここで、熱の出入りが準静的過程ではなく非平衡な過程が含まれる場合には熱力学的な変数が定義できないため当然エントロピーも定義できません。
しかし、過程に非平衡な状態があるからといって熱力学が使えないのかと言うとそういうわけではありません。熱力学はある熱平衡な状態から別の熱平衡状態への変化を扱う学問であるため、間に平衡状態があっても構わないのです。
ただ、非平衡状態がある場合のエントロピーは$dS=\frac{d^{\prime}Q}{T}$ではなく、$dS>\frac{d^{\prime}Q}{T}$となります。
つまり、準静的過程で定義できる熱力学の変数$\frac{d^{\prime}Q}{T}$（左辺）よりもエントロピーは増えていますよということです。
言い換えると自然に変化する過程において非平衡な状態があればエントロピーは増えるということです。
そして、非平衡な過程があると自然には元に戻らない不可逆性となります。
- エントロピーは$dS=\frac{d^{\prime}Q}{T}$と定義する。
- 自然に変する過程で非平衡な状態があればエントロピーは増える。
- 孤立系において状態量であるエントロピーを計算するとして、エントロピーの大きい状態に自発的に変化する。
エントロピーの定義を上記のようにすることを認めましょう。
断熱自由膨張は不可逆過程
エントロピーの意味を深く追求していくと何を考えているのかわからなくなるため、ここでは意味よりもエントロピーを$dS=\frac{d^{\prime}Q}{T}$を使って、感覚的に自発的に起こりうる現象と認識している現象に対してエントロピーを計算してみて「不可逆な変化の場合にはエネトロピーが増加している」というのを見てみましょう。
以下のような断熱自由膨張を考えます。
ところで断熱自由膨張においてエントロピー変化はどうなるでしょうか？
エントロピーが$dS=\frac{d^{\prime}Q}{T}$なので、断熱変化なら熱の出入りがないので$d^{\prime}Q=0$だからエントロピー変化はないと思った方もいるでしょう。
断熱自由膨張は断熱なのでエントロピー変化はありません。
— カマキリ🐲Python頑張る昆虫 (@t_kun_kamakiri) December 20, 2021
断熱自由膨張においてエントロピー変化はないと考える方が少々いるようですね。
実際には理論上エントロピーは増える結果になります。
「断熱過程で熱の出入りがないのになぜ？」と思う方がいるかもしれませんが、熱力学において物理量が定義できるのが熱平衡状態であることを忘れているからですね。
以下で断熱自由膨張を例にとって詳しく解説を行います。
断熱自由膨張での温度変化はなし
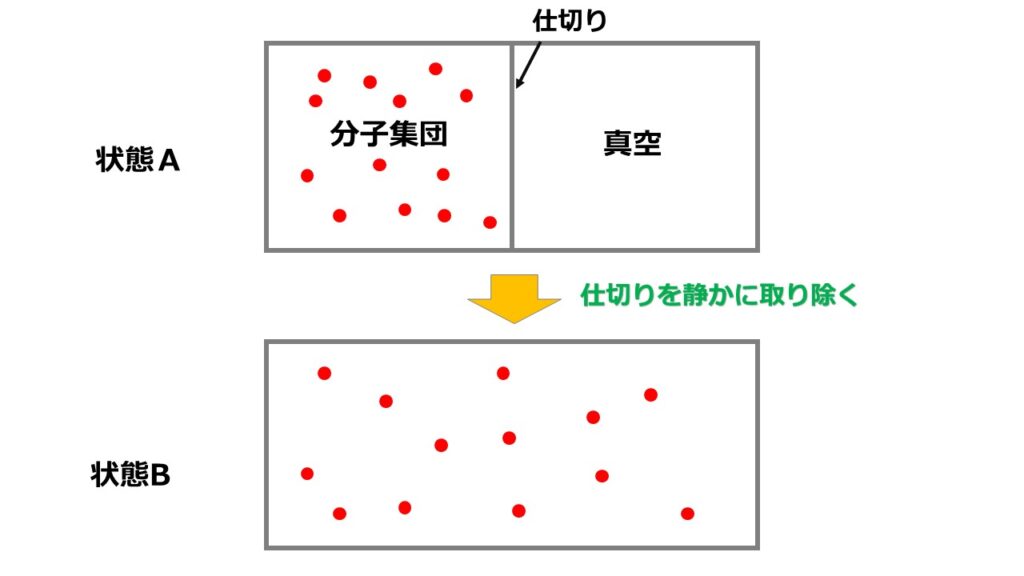
断熱自由膨張とは以下のような過程です。
状態A
左側の部屋には気体分子を詰め込んでおき、右側の部屋は真空状態にしておきます。
全体の容器は断熱材でできているため熱の出入りはありません。
さらに2つの部屋は仕切りで区切られているため分子は左の部屋のみ存在するとします。この状態で熱平衡状態であるため熱力学的である物理量（圧力$p$,温度$T$, エントロピー$S$）を定義することができます。
状態B
状態Aから変に力を加えたり摩擦熱が生じないように細心の注意を払うことにして仕切りを静かに取り除きます。
するとどうなるでしょう？左の部屋に溜まっていた分子集団がずっと左に固まっているという状態はありえないですよね。最終状態の状態Bでは分子が右の部屋にも広がって均一化します。
※気体分子は理想気体として扱えるとします。
ちなみに状態Aの左の部屋の温度を$T_{A}$とすると、状態Bでの温度$T_{B}$はどうなっているでしょうか？
状態変化後の温度って何で決まるのかを熱力学第一法則から解説しているのでご参考ください。
結論、状態Aの温度と状態Bの温度は同じです。
なぜでしょうか？
これは熱力学第一法則から簡単に導くことができます。
$$d^{\prime}Q=dU+dW\tag{1}$$
まず断熱過程であるため左辺の熱の出入りはなく$d^{\prime}Q=0$となり、$0=dU+dW$となります。
次に状態Bへの変化の過程は真空状態への膨張であるため抵抗なく気体分子は広がることができます。
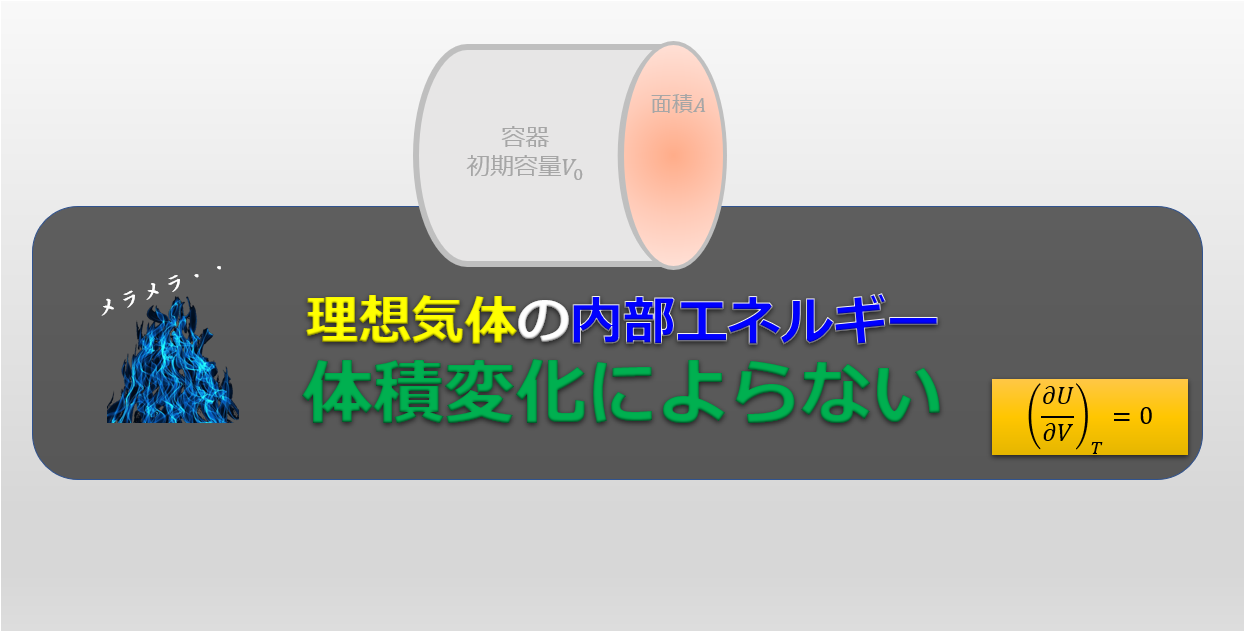
よって、内部エネルギー変化は0（$dU=0$）となります。
さらに、今考えている気体分子が理想気体で扱えると考えると、内部エネルギーは温度にのみ依存するため、内部エネルギーがないということは温度変化もないということになります。
ゆえに、
$$T_{A}=T_{B}$$となります。
断熱自由膨張でエントロピーは増加する
では、断熱自由膨張でのエントロピー変化を計算してみましょう。
しかし、断熱自由膨張には状態Bになるまでに非平衡な過程が存在します。
ということは、過程においてエントロピーも定義できず計算ができません。
どう考えたらいいのか？
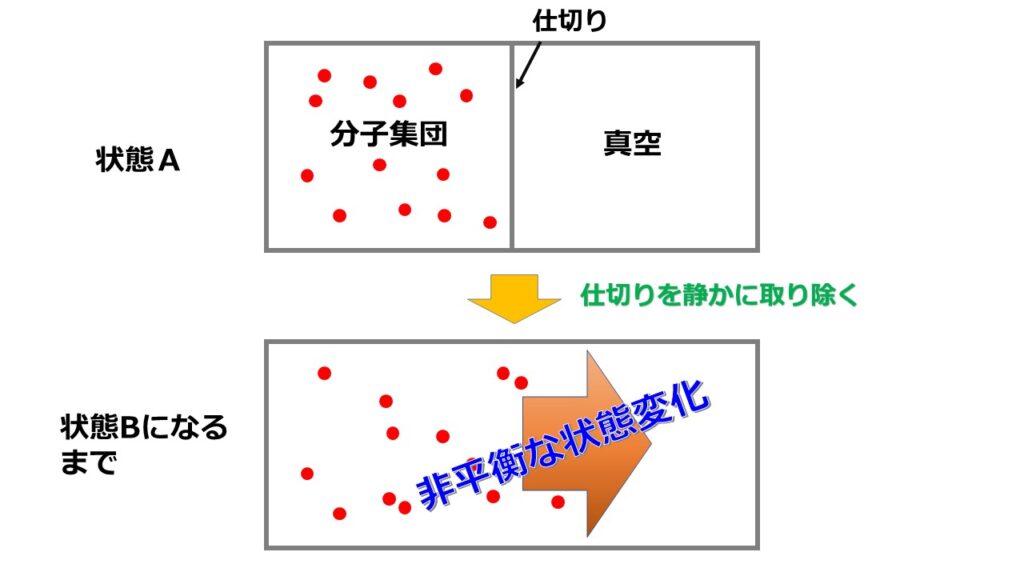
幸いなことに熱力学は間に非平衡な過程があったとしても、最終的に状態Bで熱平衡状態になってさえいれば熱力学的な状態量が定義できるためエントロピーも定義できます。
ならば、状態Bでの熱力学的な状態量さえ同じであればどんな過程を辿ったかによらずエントロピーが計算できることになります。
エントロピーは状態量なのでそのときの圧力$p$、体積$V$、温度$T$などが決まっていれば、どんな過程でその状態になったかに依らず、熱力学的な状態が確定しています。
つまり、状態Aから状態Bまでの過程は断熱自由膨張ではないけれど、準静的な過程で常に熱平衡状態が保たれており熱力学的な変数が定義できる過程を考えてエントロピー変化を計算すればよいという発想になります。
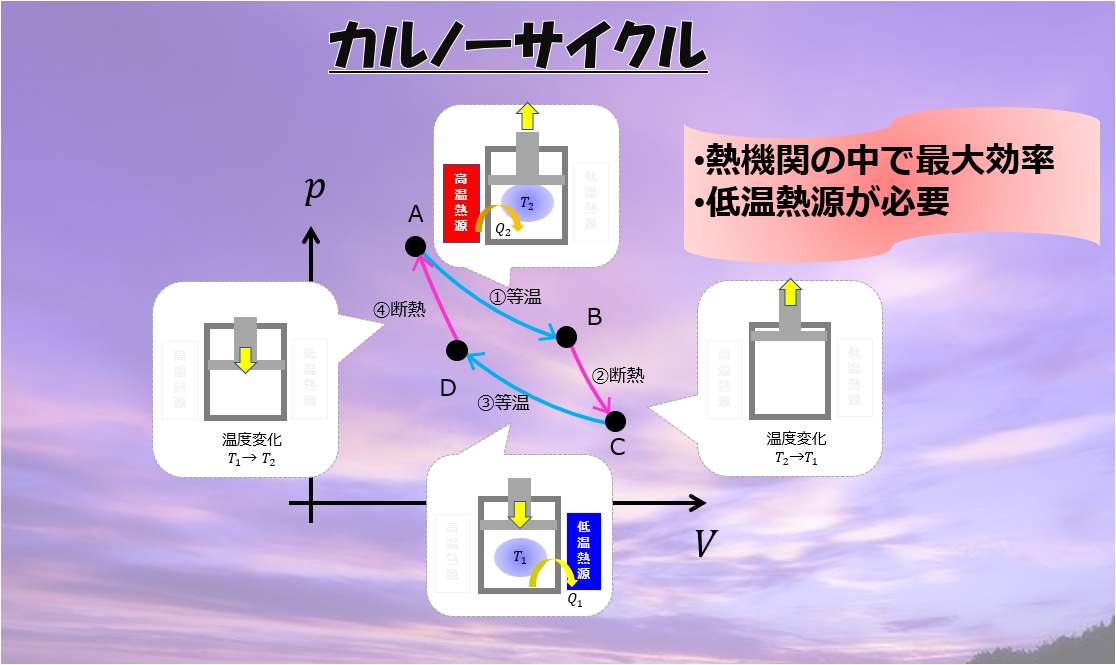
状態Aから状態Bへの準静的過程は以下のものがあります。
- 等温過程
- 等積・等圧過程
どちらも状態Aからはじまって状態Bで終わるためエントロピー変化は同じです。
以下で具体的に計算してみましょう。
等温過程でエントロピーを計算
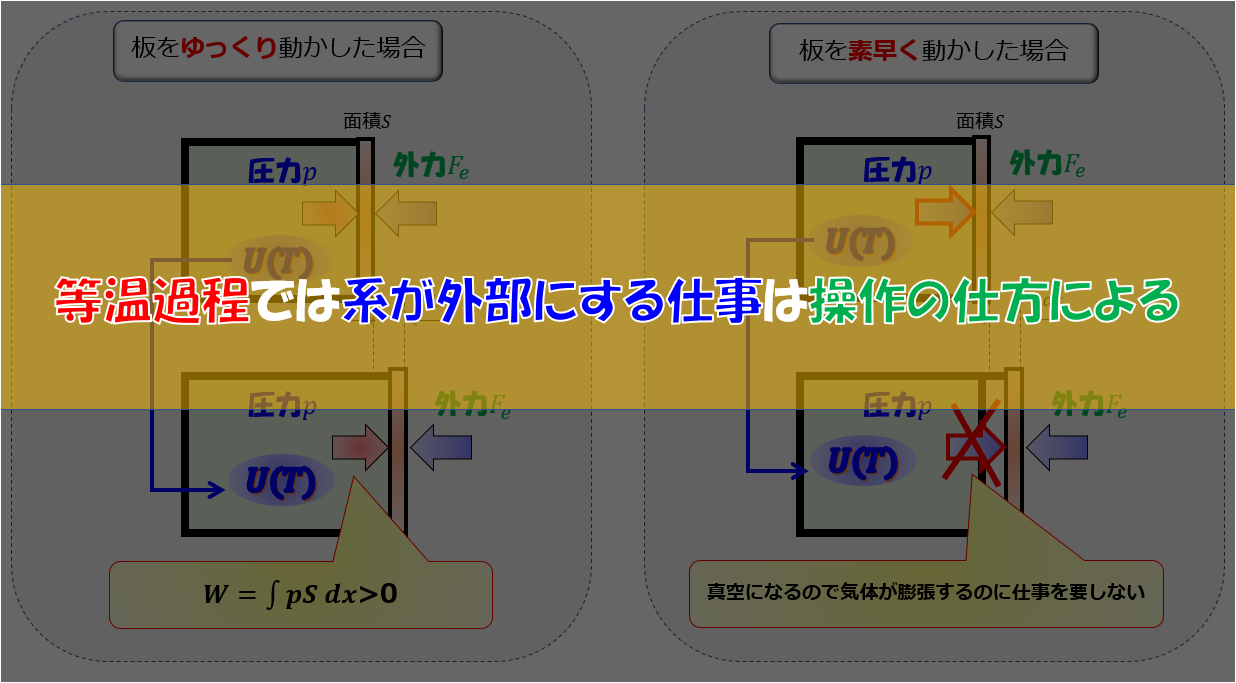
断熱自由膨張は途中で非平衡な状態がありましたが、状態Aと状態Bの温度が同じで体積が同じであれば良いのであれば、準静的過程で等温過程を考えてエントロピー変化を計算してもおねじですよね。
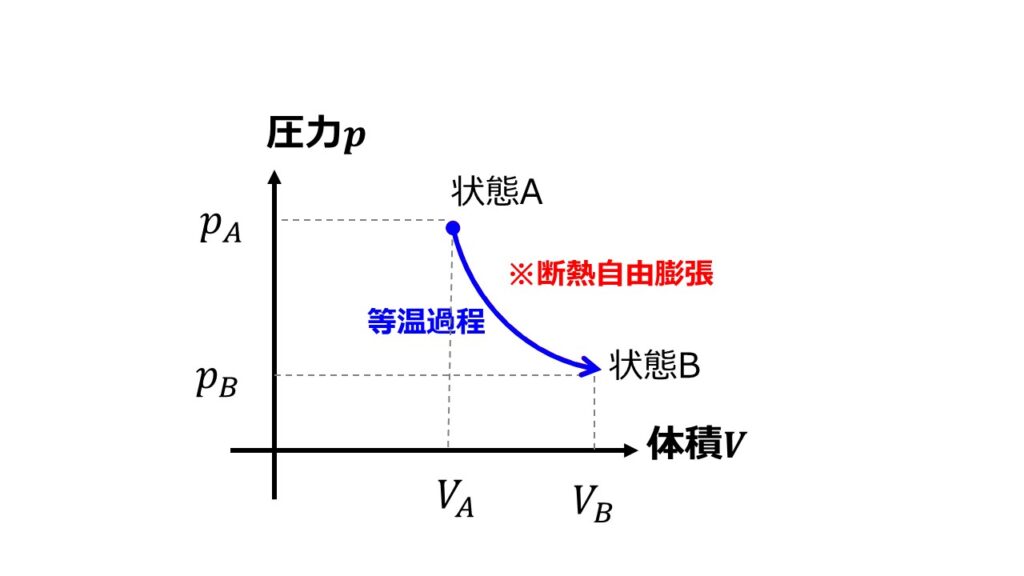
2点注意することがあります。
- 膨張させる体積容器は静かに→準静的過程のため
- 熱量$Q$を静かに加え続ける→温度を一定のため
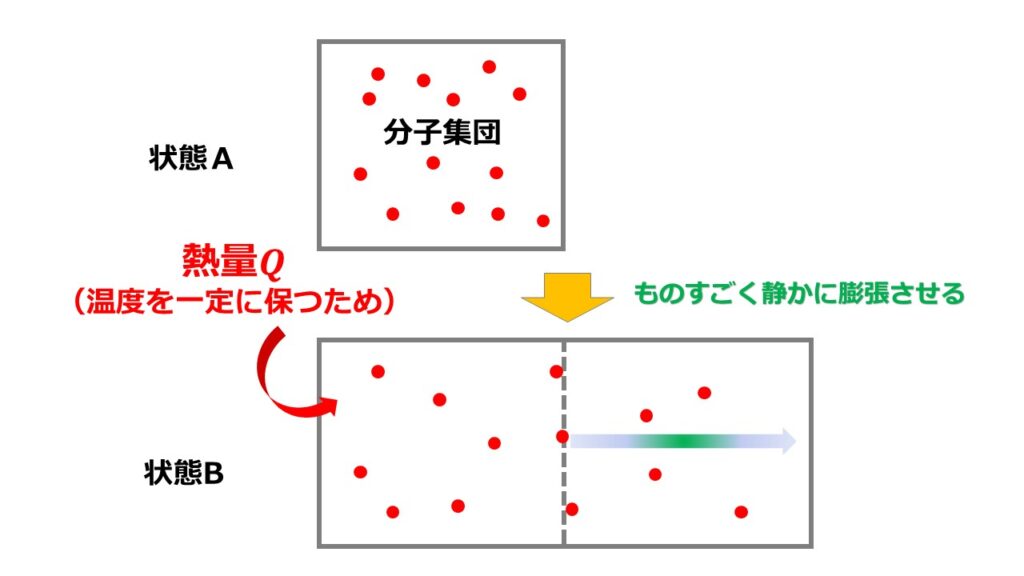
体積膨張するときに気体分子は膨張のためにエネルギーを使うため温度が下がります。
しかし、最終の温度は変わらないようにしなくてはいけないので熱量$Q$を静かに加え続ける必要があります。
では、エントロピーを計算してみましょう。
熱力学の第一法則から
$$d^{\prime}Q=dU+d^{\prime}W\tag{2}$$
$dS=\frac{d^{\prime}Q}{T}$より、
$$dS=\frac{dU}{T}+\frac{d^{\prime}W}{T}\tag{3}$$
$dU=nC_{V}dT$（定積比熱$C_{V}$）、$d^{\prime}W=pdV$、温度$T$は一定であることに注意して、(3)を積分して
$$dS=\frac{1}{T}\int_{T_{A}}^{T_{B}}nC_{V}dT+\frac{1}{T}\int_{V_{A}}^{V_{B}}pdV\tag{4}$$
ここで理想気体の状態方程式$pV=nRT$を用いると、第二項が$\int_{V_{A}}^{V_{B}}pdV=\int_{T_{A}}^{T_{B}}\frac{nR}{V}dV=n\log_{e}\big(\frac{V_{B}}{V_{A}}\big)$となります。
ここで、定積比熱$C_{V}$は本来は温度依存性がありますが、温度依存性が無視できる温度領域の範囲で考えると、(4)の第一項は$\frac{nC_{V}}{T}\big(T_{B}-T_{A})$となり$T_{A}=T_{B}$だから0になります。
よってエントロピー変化は
$$dS=n\log_{e}\bigg(\frac{V_{B}}{V_{A}}\bigg)\tag{5}$$
体積$V_{B}>V_{A}$なので、エントロピーは$dS>0$と増加しています。
つまり状態Aから状態Bへの過程は自然に起こりうる過程としては不可逆過程になります。
もちろん、仕事や熱を加えて同じ等温過程により元に戻すことはできますが、断熱自由膨張のように手を加えずに自然に起こりうる変化としては手を加えなかったら元に戻ることがありません。
このことを不可逆性の指標であるエントロピーが増加していることにより定量的に示すことができたということです。
等積・等圧過程でエントロピーを計算
エントロピーの計算には最終状態の状態量さえおなじであれば良いということであれば以下のような過程を経たエントロピー変化を計算しても良いでしょう。
- 等積過程：体積一定のまま圧力を下げる
- 定圧過程：圧力一定のまま体積を大きくする
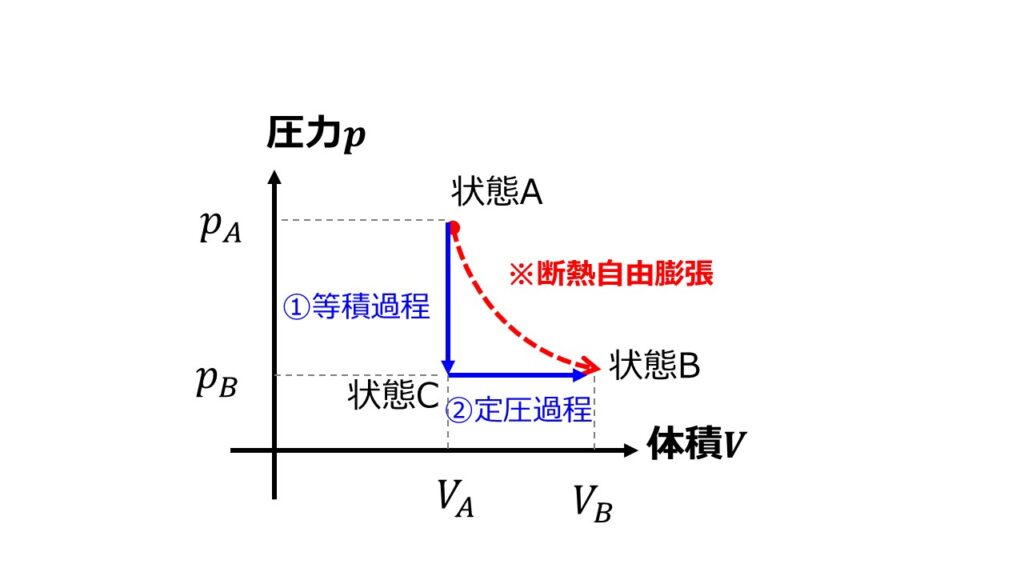
①等積過程について
体積を一定のまま圧力を下げるので温度を下げる必要があります。
そのため熱量を容器から取り除く形になります。
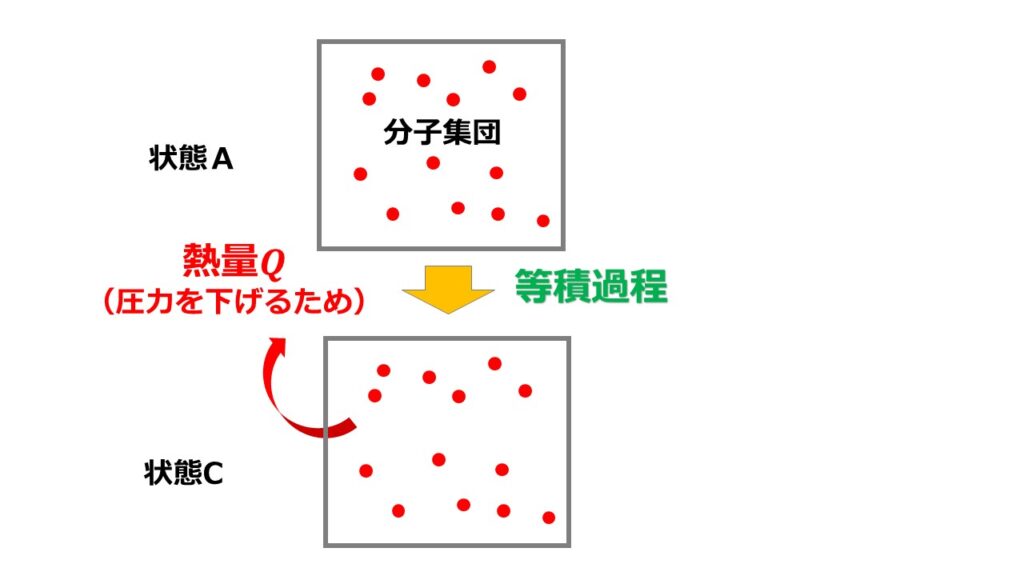
このときのエントロピー$dS_{AC}$変化を考えましょう。
得た熱量を$d^{\prime}Q$とします。ここでは熱量は取り除かれているので$Q_{AC}<0$であるが計算の結果で正負がわかるので定義通り書くことにします。
状態Aから状態Cへの変化の過程で以下のエントロピー変化が定義できます。
$$dS=\int \frac{d^{\prime}Q}{T}\tag{6}$$
熱力学第一法則より、体積変化がないため外への仕事$d^{\prime}W=0$なので、
$$d^{\prime}Q=dU\tag{7}$$となります。
ここで、内部エネルギー変化$dU=nC_{V}dT$となります。
よって、エントロピー変化は
dS_{AC}&=\int^{T_{C}}_{T_{A}} \frac{nC_{V}dT}{T}\\
&=nC_{V}\log_{e}\bigg(\frac{T_{C}}{T_{A}}\bigg)\tag{9}
\end{align*}
$T_{C}<T_{A}$なので(8)だけの過程ならエントロピーは減っているという結果です
エントロピー増大の法則という言葉を聞いたことがある方がいるかと思いますが、エントロピーは熱を取り除くことで減らすことができるのです。
必ずエントロピーが増えるという思い込みはこの計算結果で改めるべきでしょう(‘ω’)
①等圧過程について
圧力を一定のまま体積を大きくするため熱量を容器に注入する必要があります。
体積膨張によって気体分子は外に仕事をするのに、それでも圧力を一定に保つのですから多くの熱量を注入しているイメージになるでしょう。
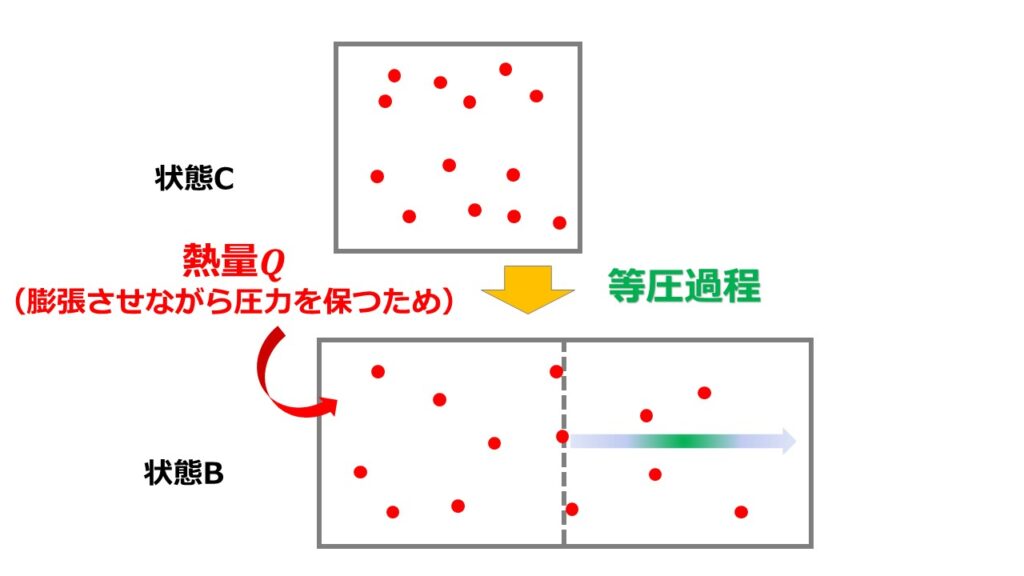
では、状態Cから状態Bへのエントロピー変化を計算してみましょう。
熱力学第一法則は以下のように書けます。
$$d^{\prime}Q=dU+pdV\tag{9}$$
$dU=nC_{V}dT$と$pV=nRT$を使うと(9)は、$d^{\prime}Q=nC_{V}dT+\frac{nRT}{V}dV$となります。
よって、エントロピー変化は$dS=\frac{d^{\prime}Q}{T}=nC_{V}\frac{dT}{T}+\frac{nR}{V}dV$より状態Cから状態Bまで積分を行い、
dS_{CB}&=nC_{V}\int^{T_{B}}_{T_{C}} \frac{dT}{T}+nR\int_{V_{C}}^{V_{B}}\frac{dV}{V}\\
&=nC_{V}\log_{e}\bigg(\frac{T_{B}}{T_{C}}\bigg)+nR\log_{e}\bigg(\frac{V_{B}}{V_{C}}\bigg)\tag{10}
\end{align*}
第二項は$p_{B}=p_{C}$であることに注意して$p_{B}V_{B}=nRT_{B}$と$p_{C}V_{C}=nRT_{C}$を使えば、$nR\log_{e}\big(\frac{T_{C}}{T_{B}}\big)$となります。
ゆえに(10)をまとめると、
dS_{CB}&=n\big(C_{V}+R\big)\log_{e}\bigg(\frac{T_{B}}{T_{C}}\bigg)\tag{12}
\end{align*}
となります。
以下のように計算をしてもいいでしょう。
定圧過程なので定圧比熱$C_{p}$を使って、熱力学第一法則を$d^{\prime}Q=nC_{p}dT$と簡単に書き換えて計算しても(11)と同じ結果になります。
では、状態Aから状態Cのエントロピー変化$dS_{AC}=nC_{V}\log_{e}\big(\frac{T_{C}}{T_{A}}\big)$と、状態Cから状態Bへのエントロピー変化$dS_{CB}=nC_{p}\log_{e}\big(\frac{V_{B}}{V_{C}}\big)$とを足します。
dS_{AB}&=dS_{AC}+dS_{CB}\\
&=nC_{V}\log_{e}\bigg(\frac{T_{C}}{T_{A}}\bigg)+n\big(C_{V}+R\big)\log_{e}\bigg(\frac{T_{B}}{T_{C}}\bigg)\\
&=nC_{V}\log_{e}\bigg(\frac{T_{B}}{T_{A}}\bigg)+nR\log_{e}\bigg(\frac{T_{B}}{T_{C}}\bigg)\tag{13}
\end{align*}
断熱自由膨張なので$T_{A}=T_{B}$より第一項は0になります。
第二項は$V_{A}=V_{C}$、$p_{C}=p_{C}$であることに注意して$p_{B}V_{B}=nRT_{B}$と$p_{C}V_{C}=nRT_{C}$を使えば、$nR\log_{e}\big(\frac{V_{A}}{V_{C}}\big)$となります。
よって、状態Aから状態Bへのエントロピー変化は、
dS_{AB}=nR\log_{e}\bigg(\frac{V_{B}}{V_{A}}\bigg)\tag{14}
\end{align*}
等温過程でのエントロピー変化の結果と同じになりましたね。
やはり、エントロピーは$dS_{AB}>0$となっており状態Aから状態Bへの過程は自然に起こりうる過程としては不可逆過程になります。
不可逆性の指標であるエントロピーが増加していることにより定量的に示すことができたということです。
まとめ
本記事では断熱自由膨張でのエントロピーを計算し、エントロピーが増えることを示しました。
エントロピーは不可逆性を定量化したものであり、断熱自由膨張のような自然に起こりうる変化でエントロピーが増えるということは自然に起こりうる変化として「それが自然」ということになります。
冷めたお湯が自然に温かくなることがないという感覚的なことを定量化したものがエントロピーです。
まとめると以下となります。
不可逆性を示す指標
マクロな視点：熱力学でのエントロピーの定義：$dS=\frac{d^{\prime}Q}{T}$
Follow @t_kun_kamakiri
状態Aから状態Cのエントロピー変化の所のｄＳの式はｄがいらないと思います。
コメントありがとうございます。
エントロピー変化を表しているのでdSはΔSという状態量の変化の意味でを示しています。
自分が理解していなくお手数ですが理由を教えていただけますでしょうか。