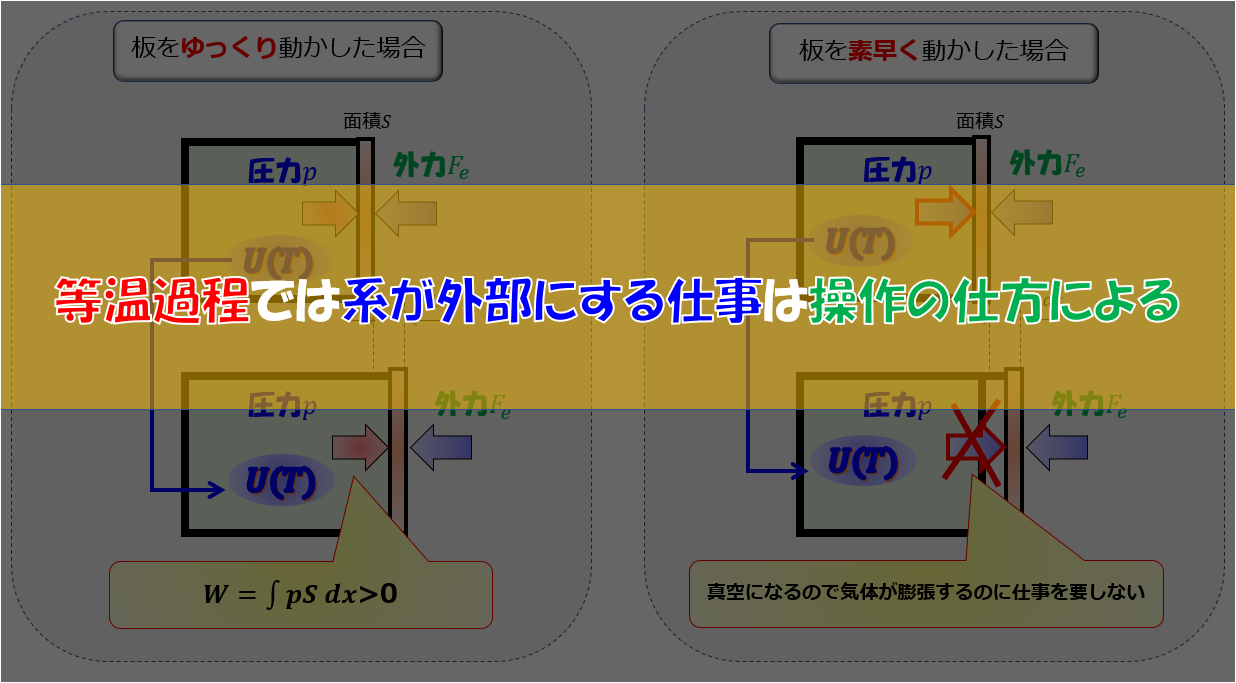
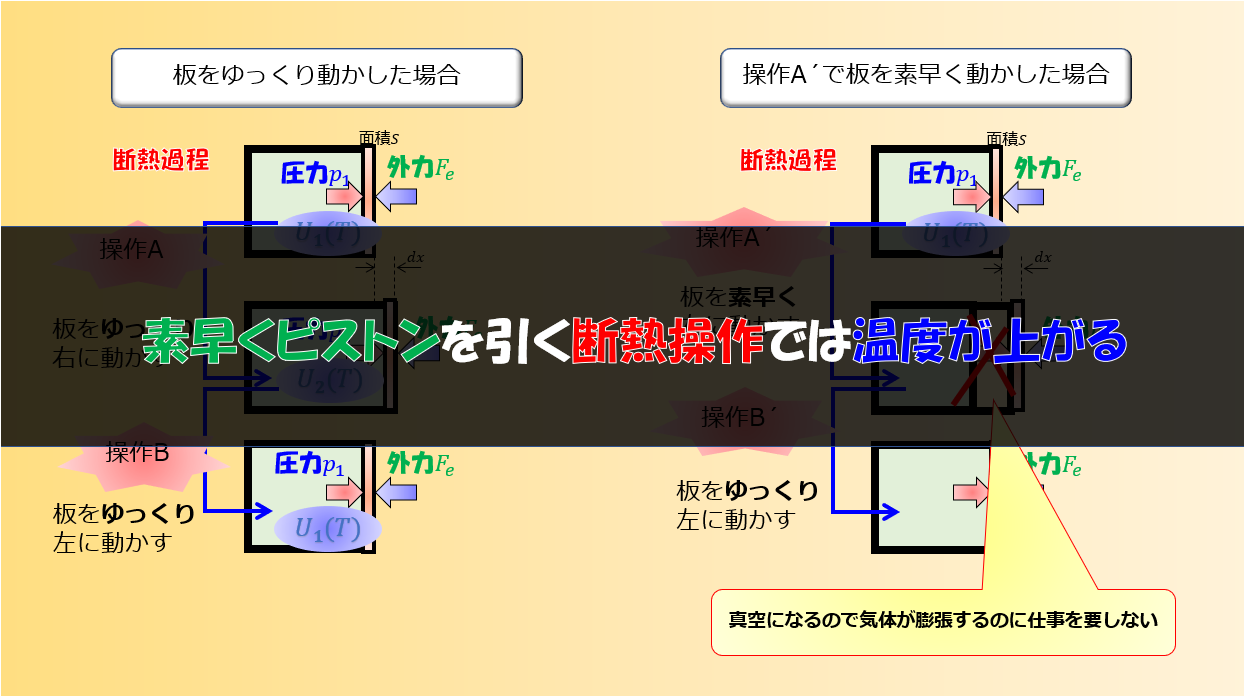
皆さん比熱に温度依存性があるのはご存知でしょうか?
熱力学では比熱は定数と考えて扱われがちですが、実際には温度依存性があります。
- 温度依存性がある場合どのように扱うのか?
- なぜ温度依存性があるのか?
定積比熱と定圧比熱の温度依存性について
「定積比熱\(C_{v}\)も定圧比熱\(C_{p}\)も一般的には温度依存性がります。(あってもおかしくない)
このような時にどのように扱えば良いのでしょうか?
その場合でも何も慌てる必要はないです・・・
理想的な状態(比熱が定数)から少しずれるのですから、ちょっと補正してやれば良いだけなのです。
ただ、どのように温度に依存するかはわからりませんよね。
線形に変化するのか、非線形か??
わからないから、とりあえず多項式で書けば良いでしょうね。
こんな感じです。
これはテーラー展開とは違うということは一応言っておきます。
テーラー展開は、「ある点のまわり(ある温度のまわり)で多項式で近似する」だけであって、全領域で適用できる展開ではないです。
ただ多項式で近似を行っただけです。
比熱の温度依存性を考慮した解析をしたい場合は、(1)(2)式の多項式の定数を物性値としてデータベース化されているのでそれを使用するだけで良いです。
空気の比熱と比熱比 参考までに
http://skomo.o.oo7.jp/f27/hp27_47.htm
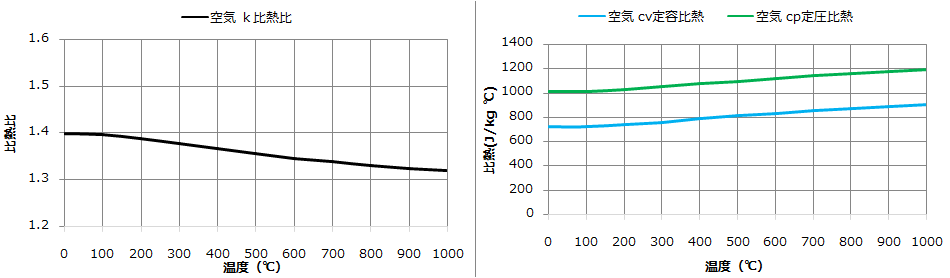
空気の「比熱比」と「定積比熱、定圧比熱」を載せておきました。
なぜ、「比熱比は温度」とともに下がり、「比熱」は温度とともに上昇していくのでしょうか。
比熱の温度依存性について理論的にまとめました。
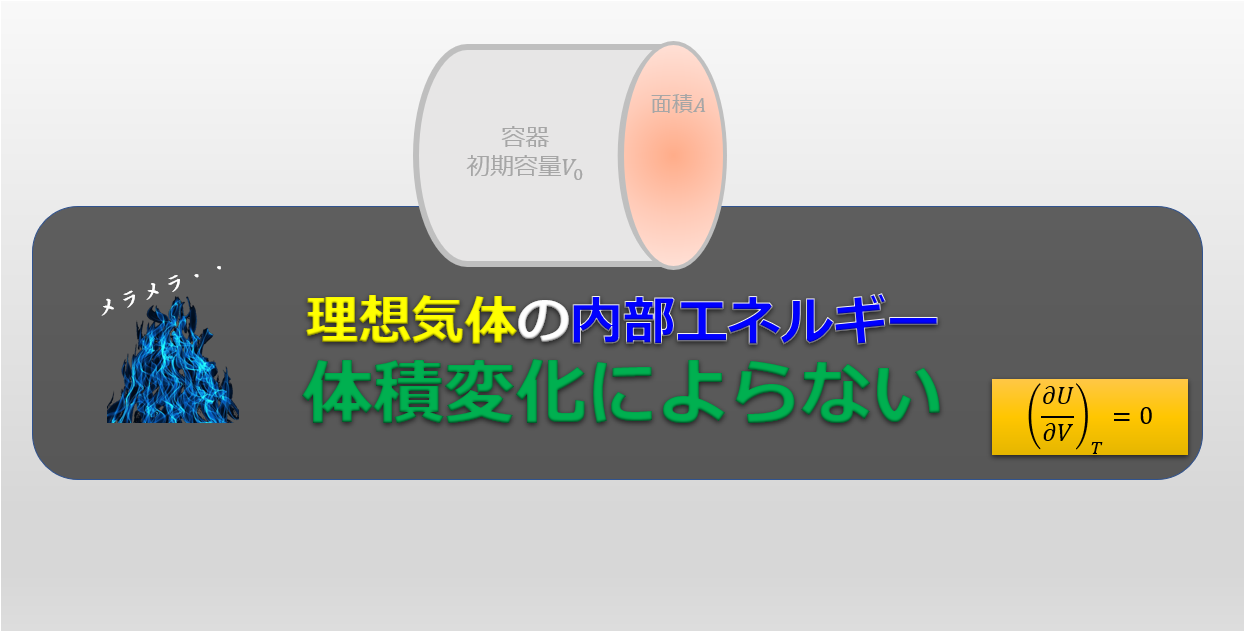
- 内部エネルギーとは何か?
【理想気体の比熱の温度依存性(1)】内部エネルギーとは。
- 古典近似での比熱の理解の誤り
【理想気体の比熱の温度依存性(2)】分配関数から物理量の期待値が求まる。
【理想気体の比熱の温度依存性(3)】分配関数の古典近似を考えてみよう。
【理想気体の比熱の温度依存性(4)】古典近似から2原子分子の比熱を求める。
【理想気体の比熱の温度依存性(5)】2原子分子の回転の運動にもエネルギーが等分配されているのか。 - 量子論(+統計力学)での比熱の取り扱いと正しい理解
【理想気体の比熱の温度依存性(6)】2原子分子のシュレディンガー方程式
【理想気体の比熱の温度依存性(7)】シュレディンガー方程式の極座標表記(2原子分子)
【理想気体の比熱の温度依存性(8)】量子論でエネルギー固有値から2原子分子の比熱を計算する
比熱の温度依存性を理解する理論的な面白さは以下にあります。
お勧めの参考書
「なぜ比熱の温度依存性があるのか」について、
- 熱力学
- 量子力学
- 統計力学
この3つの知識が必要になります。
熱力学
比熱の理解は、やはり熱力学から勉強しないといけません。
そんな中どの「熱力学」の参考書で勉強すればよいのかというと、以下の2冊が絶対おすすめです。
こちらの2冊を読むと熱力学の見方が変わります!!
量子力学
比熱の理解には量子力学の知識が絶対に必要になります。
量子力学の計算をとても丁寧に解説した参考書が以下になります。
特に「2原子分子のシュレディンガー方程式」についての解説や、「シュレディンガー方程式の極座標表記」については、下記の参考書はとても役に立ちます。
統計力学
統計力学は特に「統計力学Ⅰ」の参考書が比熱の理解には大いに役に立ちます。
量子力学の知識がある方は読み進めることができると思います。