こんにちは(@t_kun_kamakiri)(^^)/
この記事ではフーリエ変換の意味について説明したいと思います！
フーリエ変換の意味：異なる波数の波がどれくらい含んでいるかがわかる
フーリエ変換の意味するところは何かということを理解して覚えておきましょう(^^)/
結論から先に述べると・・・
例えば、\(f(x)\)が以下のような複雑な形をしているとします。
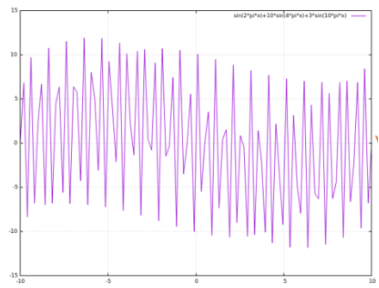
これは、実は、
という正弦波での重ね合わせで表現しているものです。
フーリエ変換は、上記のように関数\(f(x)\)を、\(\sin\)波や\(\cos\)波や正弦波\(e^{ikx}\)などの、異なる波数の波に分解して波の空間（波数空間）に変換する方法のことです。
こうやって考えると、「おや？\(\sin2\pi x\)(周期１)の波が1個か・・・・\(\sin10\pi x\)(周期１/10)の波が10個か・・・」と、どんな波が何個存在しているか数えることができます。
- 「1個、10個、3個」とか書いたものがフーリエ変換（or フーリエ級数展開）した後の関数（波数空間での関数）のこと
- 「1個、10個、3個」は各波数の波の振幅
フーリエ変換のすごいところは、無限まで積分した値が発散しなければ（\(\int^{\infty}_{-\infty}|f(x)|\ dx<\infty\)）・・・どのような任意の関数\(f(x)\)であったとしても、
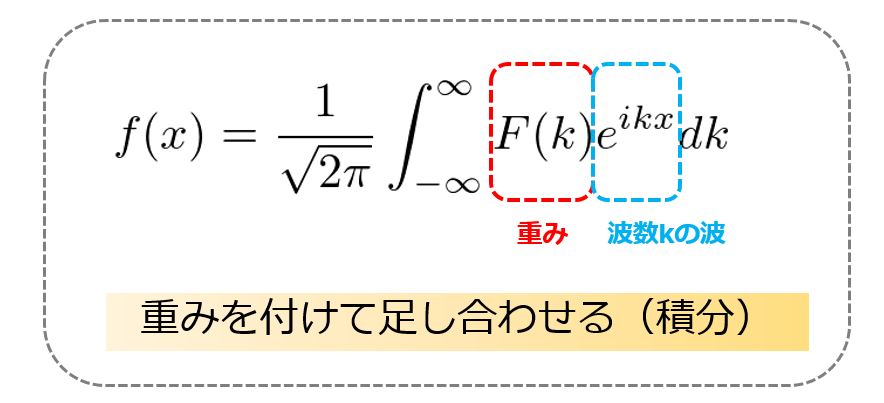
異なる波数（波の数）のものを適当な重み（どれくらい含んでいるか）をつけて足し合わせることで任意の関数\(f(x)\)を表現できるのです。
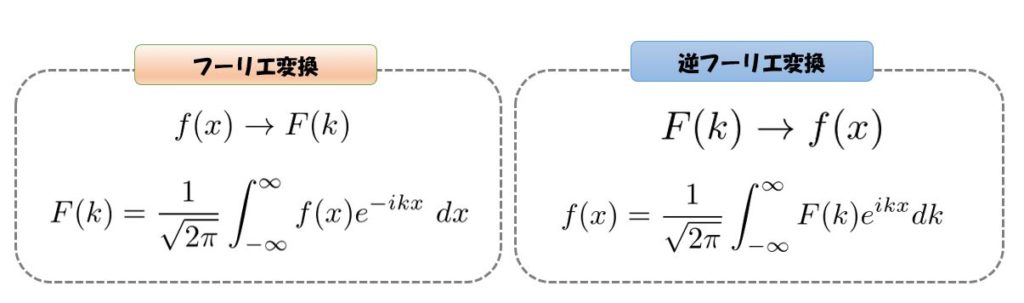
フーリエ逆変換：異なる波数で分解したものをもとの関数\(f(x)\)に戻す変換
フーリエ変換で異なる波数の波がどれくらい含んでいるかを知ることができる変換でしたが、
逆に「異なる波数がどれくらい含んでいるかを知っていた」ときに、元の関数\(f(x)\)はどのような形をしているのかを知ることができる変換がフーリエ逆変換です。
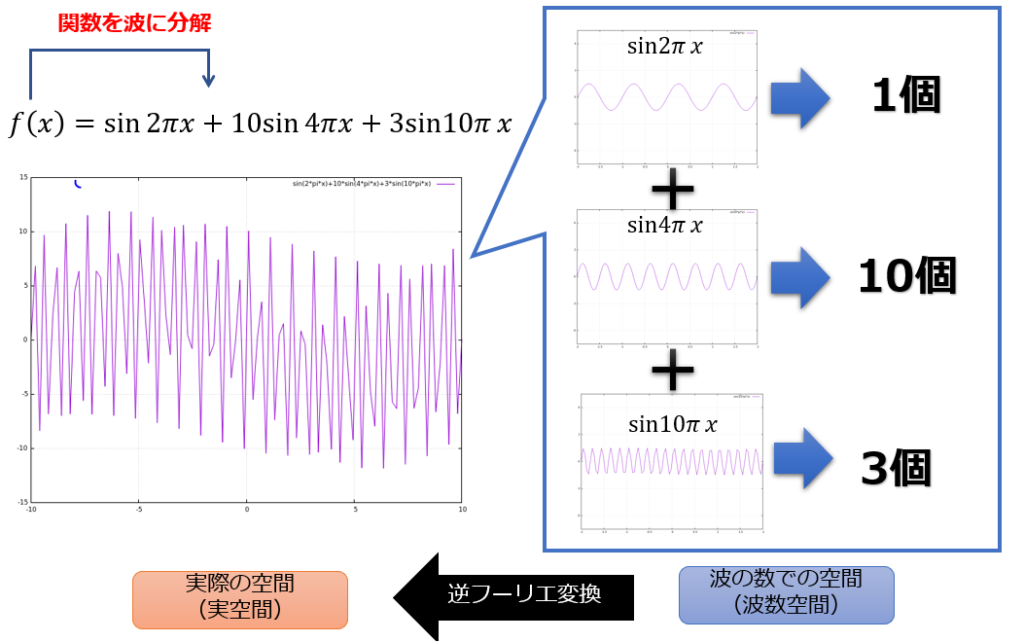
フーリエ変換と逆フーリエ変換を使うことで、「実際の空間の波\(f(x)\)」と「波の空間（波数空間）での\(F(k)\)」とを行き来することができます。
まとめ
フーリエ変換を行うことで、異なる波数の波がどれくらい含まれているかが知ることができる。
数学的な厳密な議論はしていませんが、以上が簡単な説明となります。
Follow @t_kun_kamakiri
