こんにちは(@t_kun_kamakiri)。
前回の記事では、「2次元のナビエストークス方程式」をGoogle Colab上のPythonで実装しました。
前回の記事はこちら
今回も、２次元のナビエストークス方程式をPythonで実装します。
今回の解析内容は以下のような「ポアズイユ流れ」と呼ばれる流れです。
式の詳細と数値計算の解き方については記事内で詳しく解説したいと思います(^^)/
カマキリ
流体解析は楽しいです(^^)/
本件の基本的な内容はこちらのサイトにそってやっていきます。
この記事ではこんな人を対象にしています。
こんな人が対象
- Pythonを使い始めたけどどう使うかわからない
- 流体の数値計算をはじめて勉強する人
本記事シリーズの最終目標は、ナビエストークス方程式をPythonで実装することですが、いきなりナビエストークス方程式を実装するのは難しいので各項の意味を確認しながら進めていきたいと思います。
今回の内容はこちら
２次元のナビエストークス方程式の数値計算をPythonで実装
※ポアズイユ流れ
カマキリ
今日もゆる～く学びます(^^)/
解くべき方程式の確認（ナビエストークス方程式とポアソン方程式）
まずは、今回「解くべき方程式」と「変数」が何かを確認しておきましょう。
非圧縮性流体として現象を取り扱う場合には、基本的には以下の2つの式を連立して解きます。
実際の流れは、すべての現象が(1)(2)式というわけではないで。
「ニュートン流体」「非圧縮の流れ（近似）」としているとても限定的な流れであることを理解しておきましょう。
もっと詳しく勉強したい方は☟こちらの記事を参考にしてください。
もっと詳しく勉強したい方は☟こちらの記事を参考にしてください。
前回の記事はこちら
今回は、2次元で計算を行うため少々くどいですが、成分ごとの式を書き下すことにします。
- ナビエストークスからは2本の式
- 連続の式から1つの式
が出てくるので、合計で3本の式があります。
未知数は、\(\boldsymbol{v}\)の2つと圧力\(p\)の合計3つです。
なので、原理的に未知数である物理量は全て求まることになります。
それを各時刻で求めていけば良いという事になります。
しかし、言葉で簡単に言っても、特殊な境界条件や近似を用いないとナビエストークス方程式は解析的に取り扱うことができないのです。
つまり、ナビエストークス方程式には一般解が見つかっていないので、実際には数値計算を使って偏微分方程式を取り扱うしかないのが現状です。
しかし、連立方程式を解けばいいと言われてもちょっと困った・・・
なぜなら、(3)(4)式で求めた流速は(5)式を満たす必要があります。
そのように流速を選びながら圧力を同時に決めなければなりません。
考えただけでもちょっと工夫が必要ですよね。。
そこで、以下のようにして考えを改めます。
圧力に関しては非圧縮条件を満たすようにポアソン方程式を解きつつ、求めた圧力に関してナビエストークス方程式を解き流速を求めるという手法をとります。
言葉で説明してもよくわからないかもしれないので、実際にやります(^^)/
(3)式を\(y\)で偏微分
\begin{align*}
&\frac{\partial }{\partial x}\frac{\partial u}{\partial t}+\frac{\partial u}{\partial x}\frac{\partial u}{\partial x}+u\frac{\partial^2 u}{\partial x^2}+ \frac{\partial v}{\partial x}\frac{\partial u}{\partial y}+v\frac{\partial^2 u}{\partial x\partial y} \\
&= -\frac{1}{\rho}\frac{\partial^2 p}{\partial x^2}+\nu \frac{\partial }{\partial x}\left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2} \right)\tag{6}
\end{align*}
&\frac{\partial }{\partial x}\frac{\partial u}{\partial t}+\frac{\partial u}{\partial x}\frac{\partial u}{\partial x}+u\frac{\partial^2 u}{\partial x^2}+ \frac{\partial v}{\partial x}\frac{\partial u}{\partial y}+v\frac{\partial^2 u}{\partial x\partial y} \\
&= -\frac{1}{\rho}\frac{\partial^2 p}{\partial x^2}+\nu \frac{\partial }{\partial x}\left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2} \right)\tag{6}
\end{align*}
(4)式を\(x\)で偏微分
\begin{align*}
&\frac{\partial }{\partial y}\frac{\partial v}{\partial t}+\frac{\partial u}{\partial y}\frac{\partial v}{\partial x}+u\frac{\partial^2 v}{\partial y\partial x}+ \frac{\partial v}{\partial y}\frac{\partial v}{\partial y}+v\frac{\partial^2 v}{\partial x\partial y^2} \\
&=-\frac{1}{\rho}\frac{\partial^2 p}{\partial y^2}+\nu \frac{\partial }{\partial y}\left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2} \right)\tag{7}
\end{align*}
&\frac{\partial }{\partial y}\frac{\partial v}{\partial t}+\frac{\partial u}{\partial y}\frac{\partial v}{\partial x}+u\frac{\partial^2 v}{\partial y\partial x}+ \frac{\partial v}{\partial y}\frac{\partial v}{\partial y}+v\frac{\partial^2 v}{\partial x\partial y^2} \\
&=-\frac{1}{\rho}\frac{\partial^2 p}{\partial y^2}+\nu \frac{\partial }{\partial y}\left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2} \right)\tag{7}
\end{align*}
このようにして辺々足して、非圧縮条件を使えば、
\begin{align*}
\frac{\partial^2 p}{\partial x^2}+\frac{\partial^2 p}{\partial y^2} = -\rho\left(\frac{\partial u}{\partial x}\frac{\partial u}{\partial x}+2\frac{\partial u}{\partial y}\frac{\partial v}{\partial x}+\frac{\partial v}{\partial y}\frac{\partial v}{\partial y} \right)\tag{8}
\end{align*}
\frac{\partial^2 p}{\partial x^2}+\frac{\partial^2 p}{\partial y^2} = -\rho\left(\frac{\partial u}{\partial x}\frac{\partial u}{\partial x}+2\frac{\partial u}{\partial y}\frac{\partial v}{\partial x}+\frac{\partial v}{\partial y}\frac{\partial v}{\partial y} \right)\tag{8}
\end{align*}
計算はだるいですが、一度やってみてください。
つまり、(3)(4)(5)を解く代わりに以下の式を解けばよいという事になります。
速度にいては、ナビエストークス方程式を解きつつ、圧力に対してポアソン方程式を連立させながら解くという事になります。
ポアソン方程式の解き方については、以下の記事で解説していますのでまだ読んでいない方はお読みください_(._.)_
では、解くべき方程式がわかったところで、(3)(4)(8.1)(8.2)を離散化して数値計算ができる状態にします。
解くべき方程式の離散化
【2次元での計算】※実際に解く方程式
ナビエストークス方程式
\begin{align*}
& \frac{u_{i,j}^{n+1}-u_{i,j}^{n}}{\Delta t}+u_{i,j}^{n}\frac{u_{i,j}^{n}-u_{i-1,j}^{n}}{\Delta x}+v_{i,j}^{n}\frac{u_{i,j}^{n}-u_{i,j-1}^{n}}{\Delta y} = \\
& \qquad -\frac{1}{\rho}\frac{p_{i+1,j}^{n+1}-p_{i-1,j}^{n+1}}{2\Delta x}+\nu\left(\frac{u_{i+1,j}^{n}-2u_{i,j}^{n}+u_{i-1,j}^{n}}{\Delta
x^2}+\frac{u_{i,j+1}^{n}-2u_{i,j}^{n}+u_{i,j-1}^{n}}{\Delta y^2}+F_{i,j}\right)\tag{9}
\end{align*}
& \frac{u_{i,j}^{n+1}-u_{i,j}^{n}}{\Delta t}+u_{i,j}^{n}\frac{u_{i,j}^{n}-u_{i-1,j}^{n}}{\Delta x}+v_{i,j}^{n}\frac{u_{i,j}^{n}-u_{i,j-1}^{n}}{\Delta y} = \\
& \qquad -\frac{1}{\rho}\frac{p_{i+1,j}^{n+1}-p_{i-1,j}^{n+1}}{2\Delta x}+\nu\left(\frac{u_{i+1,j}^{n}-2u_{i,j}^{n}+u_{i-1,j}^{n}}{\Delta
x^2}+\frac{u_{i,j+1}^{n}-2u_{i,j}^{n}+u_{i,j-1}^{n}}{\Delta y^2}+F_{i,j}\right)\tag{9}
\end{align*}
\begin{align*}
&\frac{v_{i,j}^{n+1}-v_{i,j}^{n}}{\Delta t}+u_{i,j}^{n}\frac{v_{i,j}^{n}-v_{i-1,j}^{n}}{\Delta x}+v_{i,j}^{n}\frac{v_{i,j}^{n}-v_{i,j-1}^{n}}{\Delta y} = \\
& \qquad -\frac{1}{\rho}\frac{p_{i,j+1}^{n+1}-p_{i,j-1}^{n+1}}{2\Delta y}+\nu\left(\frac{v_{i+1,j}^{n}-2v_{i,j}^{n}+v_{i-1,j}^{n}}{\Delta x^2}+\frac{v_{i,j+1}^{n}-2v_{i,j}^{n}+v_{i,j-1}^{n}}{\Delta y^2}\right)\tag{10}
\end{align*}
&\frac{v_{i,j}^{n+1}-v_{i,j}^{n}}{\Delta t}+u_{i,j}^{n}\frac{v_{i,j}^{n}-v_{i-1,j}^{n}}{\Delta x}+v_{i,j}^{n}\frac{v_{i,j}^{n}-v_{i,j-1}^{n}}{\Delta y} = \\
& \qquad -\frac{1}{\rho}\frac{p_{i,j+1}^{n+1}-p_{i,j-1}^{n+1}}{2\Delta y}+\nu\left(\frac{v_{i+1,j}^{n}-2v_{i,j}^{n}+v_{i-1,j}^{n}}{\Delta x^2}+\frac{v_{i,j+1}^{n}-2v_{i,j}^{n}+v_{i,j-1}^{n}}{\Delta y^2}\right)\tag{10}
\end{align*}
ポアソン方程式※連続の式（非圧縮条件）
\begin{align*}
\frac{p_{i+1,j}^{n+1}-2p_{i,j}^{n+1}+p_{i-1,j}^{n}}{\Delta x^2}+\frac{p_{i,j+1}^{n+1}-2p_{i,j}^{n+1}+p_{i,j-1}^{n+1}}{\Delta y^2} = b_{i,j}^{n}\tag{11.1}
\end{align*}
\frac{p_{i+1,j}^{n+1}-2p_{i,j}^{n+1}+p_{i-1,j}^{n}}{\Delta x^2}+\frac{p_{i,j+1}^{n+1}-2p_{i,j}^{n+1}+p_{i,j-1}^{n+1}}{\Delta y^2} = b_{i,j}^{n}\tag{11.1}
\end{align*}
\begin{align*}
b_{i,j}^{n} = \rho \left[ \frac{1}{\Delta t}\left(\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}+\frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\right)\\
-\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}\\
– 2\frac{u_{i,j+1}^{n}-u_{i,j-1}^{n}}{2\Delta y}\frac{v_{i+1,j}^{n}-v_{i-1,j}^{n}}{2\Delta x}\\
– \frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\right]\tag{11.2}
\end{align*}
b_{i,j}^{n} = \rho \left[ \frac{1}{\Delta t}\left(\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}+\frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\right)\\
-\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}\\
– 2\frac{u_{i,j+1}^{n}-u_{i,j-1}^{n}}{2\Delta y}\frac{v_{i+1,j}^{n}-v_{i-1,j}^{n}}{2\Delta x}\\
– \frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\right]\tag{11.2}
\end{align*}
どういった離散化をしているのかを以下でまとめておきました。
※絵の中で外力である\(F_{i,j}\)は省略しています。
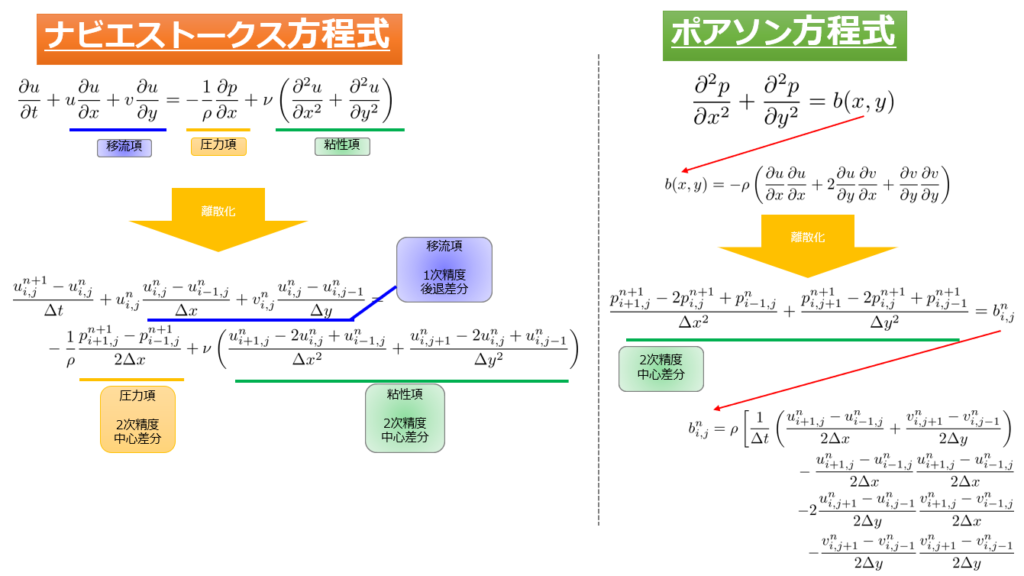
これで離散化は完了ですが、知りたいのは\(n+1\)ステップでの格子点\(i,j\)の流速\(u^{n+1}_{ij}\)、\(v^{n+1}_{ij}\)、圧力\(p^{n+1}_{ij}\)ですので、
以下のように式変形します。
【2次元での計算】※実際に解く方程式
ナビエストークス方程式
\begin{align*}
u_{i,j}^{n+1} = u_{i,j}^{n} & – u_{i,j}^{n} \frac{\Delta t}{\Delta x} \left(u_{i,j}^{n}-u_{i-1,j}^{n}\right) – v_{i,j}^{n} \frac{\Delta t}{\Delta y} \left(u_{i,j}^{n}-u_{i,j-1}^{n}\right) \\
& – \frac{\Delta t}{\rho 2\Delta x} \left(p_{i+1,j}^{n}-p_{i-1,j}^{n}\right) \\
& + \nu \left(\frac{\Delta t}{\Delta x^2} \left(u_{i+1,j}^{n}-2u_{i,j}^{n}+u_{i-1,j}^{n}\right) + \frac{\Delta t}{\Delta y^2}
\left(u_{i,j+1}^{n}-2u_{i,j}^{n}+u_{i,j-1}^{n}\right)\right)+F_{i,j}\tag{12}
\end{align*}
u_{i,j}^{n+1} = u_{i,j}^{n} & – u_{i,j}^{n} \frac{\Delta t}{\Delta x} \left(u_{i,j}^{n}-u_{i-1,j}^{n}\right) – v_{i,j}^{n} \frac{\Delta t}{\Delta y} \left(u_{i,j}^{n}-u_{i,j-1}^{n}\right) \\
& – \frac{\Delta t}{\rho 2\Delta x} \left(p_{i+1,j}^{n}-p_{i-1,j}^{n}\right) \\
& + \nu \left(\frac{\Delta t}{\Delta x^2} \left(u_{i+1,j}^{n}-2u_{i,j}^{n}+u_{i-1,j}^{n}\right) + \frac{\Delta t}{\Delta y^2}
\left(u_{i,j+1}^{n}-2u_{i,j}^{n}+u_{i,j-1}^{n}\right)\right)+F_{i,j}\tag{12}
\end{align*}
\begin{align*}
v_{i,j}^{n+1} = v_{i,j}^{n} & – u_{i,j}^{n} \frac{\Delta t}{\Delta x} \left(v_{i,j}^{n}-v_{i-1,j}^{n}\right) – v_{i,j}^{n} \frac{\Delta t}{\Delta y} \left(v_{i,j}^{n}-v_{i,j-1}^{n})\right) \\
& – \frac{\Delta t}{\rho 2\Delta y} \left(p_{i,j+1}^{n+1}-p_{i,j-1}^{n+1}\right) \\
& + \nu \left(\frac{\Delta t}{\Delta x^2} \left(v_{i+1,j}^{n}-2v_{i,j}^{n}+v_{i-1,j}^{n}\right) + \frac{\Delta t}{\Delta y^2}
\left(v_{i,j+1}^{n}-2v_{i,j}^{n}+v_{i,j-1}^{n}\right)\right)\tag{13}
\end{align*}
v_{i,j}^{n+1} = v_{i,j}^{n} & – u_{i,j}^{n} \frac{\Delta t}{\Delta x} \left(v_{i,j}^{n}-v_{i-1,j}^{n}\right) – v_{i,j}^{n} \frac{\Delta t}{\Delta y} \left(v_{i,j}^{n}-v_{i,j-1}^{n})\right) \\
& – \frac{\Delta t}{\rho 2\Delta y} \left(p_{i,j+1}^{n+1}-p_{i,j-1}^{n+1}\right) \\
& + \nu \left(\frac{\Delta t}{\Delta x^2} \left(v_{i+1,j}^{n}-2v_{i,j}^{n}+v_{i-1,j}^{n}\right) + \frac{\Delta t}{\Delta y^2}
\left(v_{i,j+1}^{n}-2v_{i,j}^{n}+v_{i,j-1}^{n}\right)\right)\tag{13}
\end{align*}
ポアソン方程式※連続の式（非圧縮条件）
\begin{align*}
p_{i,j}^{n+1}=\frac{(p_{i+1,j}^{n+1}+p_{i-1,j}^{n+1})\Delta y^2+(p_{i,j+1}^{n+1}+p_{i,j-1}^{n+1})\Delta x^2-b_{i,j}^{n}\Delta x^2\Delta y^2}{2(\Delta x^2+\Delta y^2)}
\tag{14.1}
\end{align*}
p_{i,j}^{n+1}=\frac{(p_{i+1,j}^{n+1}+p_{i-1,j}^{n+1})\Delta y^2+(p_{i,j+1}^{n+1}+p_{i,j-1}^{n+1})\Delta x^2-b_{i,j}^{n}\Delta x^2\Delta y^2}{2(\Delta x^2+\Delta y^2)}
\tag{14.1}
\end{align*}
\begin{align*}
b_{i,j}^{n} = \rho\left[\frac{1}{\Delta t}\left(\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}+\frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\right)\\
-\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}\\
-2\frac{u_{i,j+1}^{n}-u_{i,j-1}^{n}}{2\Delta y}\frac{v_{i+1,j}^{n}-v_{i-1,j}^{n}}{2\Delta x}-\\
\frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\right]\tag{14.2}
\end{align*}
b_{i,j}^{n} = \rho\left[\frac{1}{\Delta t}\left(\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}+\frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\right)\\
-\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}\\
-2\frac{u_{i,j+1}^{n}-u_{i,j-1}^{n}}{2\Delta y}\frac{v_{i+1,j}^{n}-v_{i-1,j}^{n}}{2\Delta x}-\\
\frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\right]\tag{14.2}
\end{align*}
では、これらを数値計算で解いていきましょう。
初期状態と境界条件を設定
数値計算をはじめるまえに、初期状態と境界条件を設定する必要があります。
【初期状態】
- \(u, v, p = 0\)
【境界条件】
- \(u, v, p\) at \(x=0,2\)で周期境界条件
- \(u, v =0\) at \(y =0,2\)
- \(\frac{\partial p}{\partial y}=0\) at \(y =0,2\);
- \(F=1\) everywhere
言葉だけではよくわからないかと思いますので、絵を作成しました。
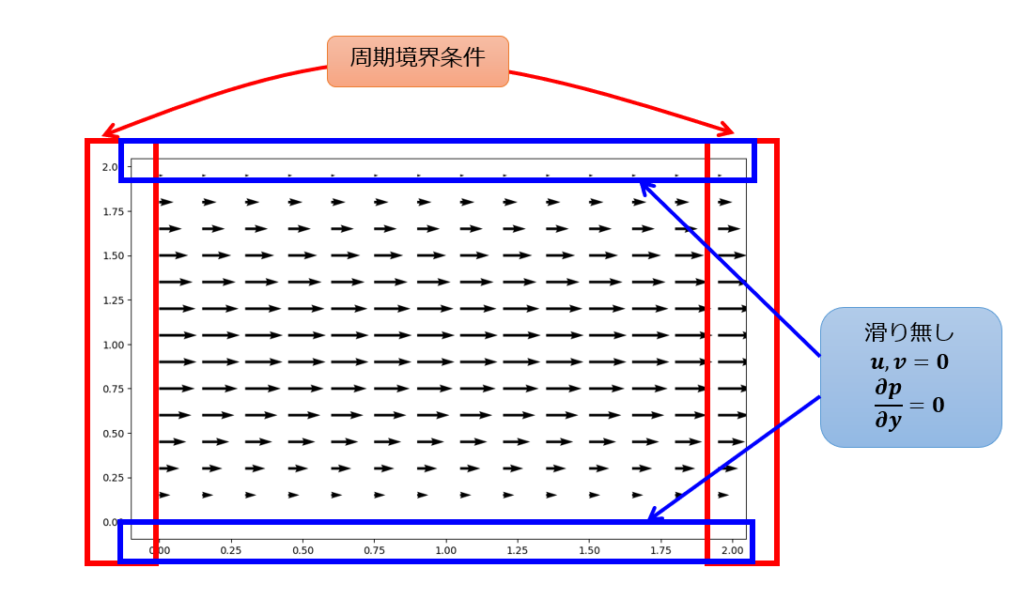
今回解析するのは「ポアズイユ流れ」と呼ばれる流れです。
※ちなみに、圧力の基準圧を\(p=0\)としています。
なので、境界条件として\(y=0\)の圧力は\(p=0\)としています。
非圧縮条件で式を解く場合は、圧力の微分の項のみしか意味がないので、基準値は何でもいいんですよね。だから、もし考えている系の基準圧を大気圧（101.25Paくらい）としている場合に、わざわざ境界条件を\(p=101.325kPa\)とする必要はありません。
境界条件に\(p=0\)としておいて、計算された圧力分布は基準圧に対してどうなのかを考えればいいだけです。
（基準圧が\(p=101.325kPa\)なら、分布に\(p=101.325kPa\)を足せばいいだけという意味です）
流体解析に関する境界条件の考え方は非常に見ずかしいので、扱う現象に応じて自身で境界条件を考える必要があります。
ここでは、詳しくは解説しませんが（体系的に解説できるほどの知識もないですが_(._.)_）以下の記事が参考になると思います。
境界条件に関する記事はこちら
では、以下で実際にナビエストークス方程式とポアソン方程式を連立させながらGoogle Colaboratoryを使ってPythonのコードを書いていきましょう。
キャビティ流れを解く手順（フロー）
ひとつひとつ解説をしながらコードを書いていきます。
※関数にまとめておいた方がいい部分は関数にまとめます。
今回行う数値計算の解く手順は以下のフローに従っています。
これは「MAC（Marker And Cell）法」と呼ばれる非圧縮流体の解析手法の一種です。
ナビエストークス方程式、およびナビエストークス方程式の発散と連続の式から得られる圧力方程式を連立して計算を行います。
ナビエストークス方程式、およびナビエストークス方程式の発散と連続の式から得られる圧力方程式を連立して計算を行います。
Pythonで実装
【ポイント】
必要なライブラリをインポートする。
必要なライブラリをインポートする。
コードを以下のように書きます。
1 2 3 4 | import numpy as np from matplotlib import pyplot as plt from matplotlib import cm from mpl_toolkits.mplot3d import Axes3D |
NumpyとMatplotlibをインポートします。
記述ミスがなければエラーなく進みます。
【ポイント】
- 条件設定（空間領域、時間刻み）
- 初期状態の設定
- 境界条件の設定
コードを以下のように書きます。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 | ##variable declarations nx = 41 ny = 41 nt = 10 nit = 50 c = 1 dx = 2 / (nx - 1) dy = 2 / (ny - 1) x = np.linspace(0, 2, nx) y = np.linspace(0, 2, ny) X, Y = np.meshgrid(x, y) ##physical variables rho = 1 nu = .1 F = 1 dt = .01 #initial conditions u = np.zeros((ny, nx)) un = np.zeros((ny, nx)) v = np.zeros((ny, nx)) vn = np.zeros((ny, nx)) p = np.ones((ny, nx)) pn = np.ones((ny, nx)) b = np.zeros((ny, nx)) |
※初期状態は実際に解く際にももう一回定義しなおすので、ここでは書かなくても良いですが・・・
ポアソン方程式の解く部分は結構煩雑なので、まずは\(b^{n}_{ij}\)に関しては以下のように関数にまとめておきます。
【ポイント】
の関数を作成する。
\begin{align*}
b_{i,j}^{n} = \rho\left[\frac{1}{\Delta t}\left(\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}+\frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\right)\\
-\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}\\
-2\frac{u_{i,j+1}^{n}-u_{i,j-1}^{n}}{2\Delta y}\frac{v_{i+1,j}^{n}-v_{i-1,j}^{n}}{2\Delta x}-\\
\frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\right]\tag{14.2}
\end{align*}
b_{i,j}^{n} = \rho\left[\frac{1}{\Delta t}\left(\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}+\frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\right)\\
-\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}\\
-2\frac{u_{i,j+1}^{n}-u_{i,j-1}^{n}}{2\Delta y}\frac{v_{i+1,j}^{n}-v_{i-1,j}^{n}}{2\Delta x}-\\
\frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\right]\tag{14.2}
\end{align*}
の関数を作成する。
コードを以下のように書きます。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | def build_up_b(rho, dt, dx, dy, u, v): b = np.zeros_like(u) b[1:-1, 1:-1] = (rho * (1 / dt * ((u[1:-1, 2:] - u[1:-1, 0:-2]) / (2 * dx) + (v[2:, 1:-1] - v[0:-2, 1:-1]) / (2 * dy)) - ((u[1:-1, 2:] - u[1:-1, 0:-2]) / (2 * dx))**2 - 2 * ((u[2:, 1:-1] - u[0:-2, 1:-1]) / (2 * dy) * (v[1:-1, 2:] - v[1:-1, 0:-2]) / (2 * dx))- ((v[2:, 1:-1] - v[0:-2, 1:-1]) / (2 * dy))**2)) # Periodic BC Pressure @ x = 2 b[1:-1, -1] = (rho * (1 / dt * ((u[1:-1, 0] - u[1:-1,-2]) / (2 * dx) + (v[2:, -1] - v[0:-2, -1]) / (2 * dy)) - ((u[1:-1, 0] - u[1:-1, -2]) / (2 * dx))**2 - 2 * ((u[2:, -1] - u[0:-2, -1]) / (2 * dy) * (v[1:-1, 0] - v[1:-1, -2]) / (2 * dx)) - ((v[2:, -1] - v[0:-2, -1]) / (2 * dy))**2)) # Periodic BC Pressure @ x = 0 b[1:-1, 0] = (rho * (1 / dt * ((u[1:-1, 1] - u[1:-1, -1]) / (2 * dx) + (v[2:, 0] - v[0:-2, 0]) / (2 * dy)) - ((u[1:-1, 1] - u[1:-1, -1]) / (2 * dx))**2 - 2 * ((u[2:, 0] - u[0:-2, 0]) / (2 * dy) * (v[1:-1, 1] - v[1:-1, -1]) / (2 * dx))- ((v[2:, 0] - v[0:-2, 0]) / (2 * dy))**2)) return b |
そして、ポアソン方程式本体は、以下のように関数としておきます。
コードを以下のように書きます。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | def pressure_poisson_periodic(p, dx, dy): pn = np.empty_like(p) for q in range(nit): pn = p.copy() p[1:-1, 1:-1] = (((pn[1:-1, 2:] + pn[1:-1, 0:-2]) * dy**2 + (pn[2:, 1:-1] + pn[0:-2, 1:-1]) * dx**2) / (2 * (dx**2 + dy**2)) - dx**2 * dy**2 / (2 * (dx**2 + dy**2)) * b[1:-1, 1:-1]) # Periodic BC Pressure @ x = 2 p[1:-1, -1] = (((pn[1:-1, 0] + pn[1:-1, -2])* dy**2 + (pn[2:, -1] + pn[0:-2, -1]) * dx**2) / (2 * (dx**2 + dy**2)) - dx**2 * dy**2 / (2 * (dx**2 + dy**2)) * b[1:-1, -1]) # Periodic BC Pressure @ x = 0 p[1:-1, 0] = (((pn[1:-1, 1] + pn[1:-1, -1])* dy**2 + (pn[2:, 0] + pn[0:-2, 0]) * dx**2) / (2 * (dx**2 + dy**2)) - dx**2 * dy**2 / (2 * (dx**2 + dy**2)) * b[1:-1, 0]) # Wall boundary conditions, pressure p[-1, :] =p[-2, :] # dp/dy = 0 at y = 2 p[0, :] = p[1, :] # dp/dy = 0 at y = 0 return p |
前回の記事でも解説しましたが、ポアソン方程式では「反復計算」による計算を行って圧力を求めています。
収束判定の方法は色々アイデアがるのですが、「ある値以下になったら収束する方法」か「ある回数反復計算したら収束したとみなす方法」のどちらかが主にやられる手法です。
今回は「nit = 50」として、50回反復計算したら収束している（であろう）として、ポアソン方程式から圧力を求めています。
では、メインの流速を求める部分を以下のように関数にまとめておきます。
コードを以下のように書きます。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 | udiff = 1 stepcount = 0 while udiff > .001: un = u.copy() vn = v.copy() b = build_up_b(rho, dt, dx, dy, u, v) p = pressure_poisson_periodic(p, dx, dy) u[1:-1, 1:-1] = (un[1:-1, 1:-1] - un[1:-1, 1:-1] * dt / dx * (un[1:-1, 1:-1] - un[1:-1, 0:-2]) - vn[1:-1, 1:-1] * dt / dy * (un[1:-1, 1:-1] - un[0:-2, 1:-1]) - dt / (2 * rho * dx) * (p[1:-1, 2:] - p[1:-1, 0:-2]) + nu * (dt / dx**2 * (un[1:-1, 2:] - 2 * un[1:-1, 1:-1] + un[1:-1, 0:-2]) + dt / dy**2 * (un[2:, 1:-1] - 2 * un[1:-1, 1:-1] + un[0:-2, 1:-1])) + F * dt) v[1:-1, 1:-1] = (vn[1:-1, 1:-1] - un[1:-1, 1:-1] * dt / dx * (vn[1:-1, 1:-1] - vn[1:-1, 0:-2]) - vn[1:-1, 1:-1] * dt / dy * (vn[1:-1, 1:-1] - vn[0:-2, 1:-1]) - dt / (2 * rho * dy) * (p[2:, 1:-1] - p[0:-2, 1:-1]) + nu * (dt / dx**2 * (vn[1:-1, 2:] - 2 * vn[1:-1, 1:-1] + vn[1:-1, 0:-2]) + dt / dy**2 * (vn[2:, 1:-1] - 2 * vn[1:-1, 1:-1] + vn[0:-2, 1:-1]))) # Periodic BC u @ x = 2 u[1:-1, -1] = (un[1:-1, -1] - un[1:-1, -1] * dt / dx * (un[1:-1, -1] - un[1:-1, -2]) - vn[1:-1, -1] * dt / dy * (un[1:-1, -1] - un[0:-2, -1]) - dt / (2 * rho * dx) * (p[1:-1, 0] - p[1:-1, -2]) + nu * (dt / dx**2 * (un[1:-1, 0] - 2 * un[1:-1,-1] + un[1:-1, -2]) + dt / dy**2 * (un[2:, -1] - 2 * un[1:-1, -1] + un[0:-2, -1])) + F * dt) # Periodic BC u @ x = 0 u[1:-1, 0] = (un[1:-1, 0] - un[1:-1, 0] * dt / dx * (un[1:-1, 0] - un[1:-1, -1]) - vn[1:-1, 0] * dt / dy * (un[1:-1, 0] - un[0:-2, 0]) - dt / (2 * rho * dx) * (p[1:-1, 1] - p[1:-1, -1]) + nu * (dt / dx**2 * (un[1:-1, 1] - 2 * un[1:-1, 0] + un[1:-1, -1]) + dt / dy**2 * (un[2:, 0] - 2 * un[1:-1, 0] + un[0:-2, 0])) + F * dt) # Periodic BC v @ x = 2 v[1:-1, -1] = (vn[1:-1, -1] - un[1:-1, -1] * dt / dx * (vn[1:-1, -1] - vn[1:-1, -2]) - vn[1:-1, -1] * dt / dy * (vn[1:-1, -1] - vn[0:-2, -1]) - dt / (2 * rho * dy) * (p[2:, -1] - p[0:-2, -1]) + nu * (dt / dx**2 * (vn[1:-1, 0] - 2 * vn[1:-1, -1] + vn[1:-1, -2]) + dt / dy**2 * (vn[2:, -1] - 2 * vn[1:-1, -1] + vn[0:-2, -1]))) # Periodic BC v @ x = 0 v[1:-1, 0] = (vn[1:-1, 0] - un[1:-1, 0] * dt / dx * (vn[1:-1, 0] - vn[1:-1, -1]) - vn[1:-1, 0] * dt / dy * (vn[1:-1, 0] - vn[0:-2, 0]) - dt / (2 * rho * dy) * (p[2:, 0] - p[0:-2, 0]) + nu * (dt / dx**2 * (vn[1:-1, 1] - 2 * vn[1:-1, 0] + vn[1:-1, -1]) + dt / dy**2 * (vn[2:, 0] - 2 * vn[1:-1, 0] + vn[0:-2, 0]))) # Wall BC: u,v = 0 @ y = 0,2 u[0, :] = 0 u[-1, :] = 0 v[0, :] = 0 v[-1, :]=0 udiff = (np.sum(u) - np.sum(un)) / np.sum(u) stepcount += 1 |
エラーなく実行できれば、何も出力されませんが、u,vの流速分布がポアズイユ流れになっています。
1 2 | #ループの回数 print(stepcount) |
【結果】
1 | 499 |
499回の反復計算の末に「udiff = (np.sum(u) – np.sum(un)) / np.sum(u)」が「0.001」より小さくなって収束したと判定しています。
結果の可視化にはMatplotlibを使います。
Matplotlibで結果を可視化する
結果の可視化は色々あるのですが、今回は流速ベクトルを見ます。
コードを以下のように書きます。
1 2 | fig = plt.figure(figsize = (11,7), dpi=100) plt.quiver(X[::3, ::3], Y[::3, ::3], u[::3, ::3], v[::3, ::3]); |
【結果】
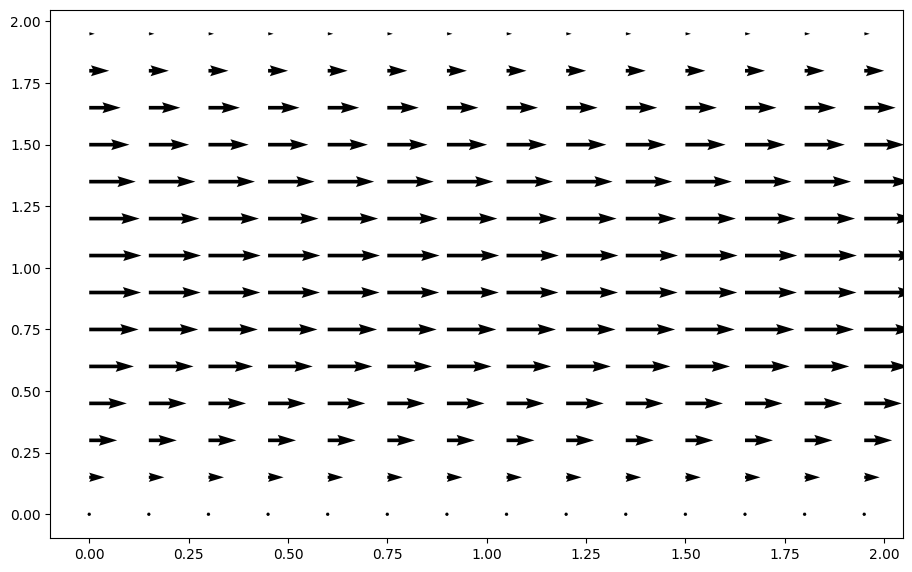
なんか、流体の数値計算をやったって気になれますね(^^)/
カマキリ
流体解析は楽しいです(^^)/
\(F\)の意味は何か？
\(x\)方向の運動量保存則
\begin{align*}
\frac{\partial u}{\partial t}+u \cdot \nabla u = -\frac{\partial p}{\partial x}+\nu \nabla^2 u
\end{align*}
\frac{\partial u}{\partial t}+u \cdot \nabla u = -\frac{\partial p}{\partial x}+\nu \nabla^2 u
\end{align*}
ここで、もし圧力を\(p=P+p^{\prime}\)のように分解したとします。
- \(P\)：安定
- \(p^{\prime}\)：不安定
そうすると、\(x\)方向の運動量保存則は、
\begin{align*}
$\frac{\partial u}{\partial t}+u \cdot \nabla u = -\frac{\partial p^{\prime}}{\partial x}+\nu \nabla^2 u-\frac{\partial P}{\partial x}
\end{align*}
$\frac{\partial u}{\partial t}+u \cdot \nabla u = -\frac{\partial p^{\prime}}{\partial x}+\nu \nabla^2 u-\frac{\partial P}{\partial x}
\end{align*}
声ⓜ\(-\frac{\partial p^{‘}}{\partial x}=F\)と考えればよい。
ここで、\(P=const\)なら\(-\frac{\partial P}{\partial x}=0\)となりますよね。
つまり、\(P\)は基準圧を意味します。
そうすると、非圧縮性流体のように「運動量保存（ナビエストークス方程式）」と「質量保存則（連続の式）」だけに従う場合は、基準圧はどうとっても良いという事になります。
だから、非圧縮性として流れを扱う場合は、「基準圧を大気圧(101325Pa)」などのデカイ数字を使うのではなく、「基準圧0Pa」とするのが一般的ですかね(‘ω’)
まとめ
今回は、2次元のナビエストークス方程式を解いてポアズイユ流れをPythonで実装してみました。
過去の今回の内容に至るまでの全ての記事は、下記にまとめていますので復習ながら学習してください_(._.)_
前回の記事はこちら
あとは、境界条件や空間領域などの設定を変更しながら流体の数値計算を楽しんでもらえればと思います。
※ただ、今回紹介したのは流体の数値計算のほんの一部の解き方だけです。
取り扱う流体現象や方程式によっては十分な精度がでなかったり、安定的に解いてくれなかったりします。
流体の数値計算を行う際は、以下の内容をきちんと学んでおく必要があります。
- プログラミング言語（Pythonなど）
- 流体力学
- 数値流体
- 数値計算
以下に、書籍の紹介をしておきます。
おすすめの書籍紹介
ネット上には無料で多くのことが学べるのですが、ネット情報だけだと情報が偏ったりします。やっぱり書籍を手に取って体系だって学んだ方が良い場合も多いです。
初心者でもので体系だって学ぶことができる、且つあまり難しすぎない書籍をここで紹介しておきます。
Pythonの完全初心者は書籍で学ぶとよい
Python自体が不安だという方は、こちらの書籍から勉強しても良いかも知れません。
☟こちらの本がPython初心者が挫折することなく勉強できる本です。
（本記事のようのPython使用環境と異なりますが、とてもわかりやすいので全く問題ありません）
僕自身もこの書籍ではじめは勉強しました。
小難しい余計なことが書いていないし、年末の一週間くらいで読むことができたので、初心者の方にはとてもお勧めです。
流体の勉強をしたい方
流体の数値計算以前に、流体力学を勉強しないと！！って思っている方は以下の参考書からはじめてみるのが良いと思います。
工学よりに書かれていて実用的な内容も触れながら、流体の理論的な内容も易しく書かれていますので大学１年生で偏微分を学んだ方にとってはちょうどよい参考書です。
数値流体の書籍
本記事で紹介している数値計算手法は、多くの数値解法のごく一部です。
特に、非線形方程式で記述できる流体現象のようなものは注意深く数値解法を選択しなくてはいけません。
以下の書籍は、値段が高いですが有限体積法をメインに数値解法がとても詳しく解説されています。
数値計算の書籍
今回紹介したポアソン方程式は「ヤコビ法」と呼ばれる反復計算を行っていますが、その他の有名な数値的解法のをいくつか挙げておきます。
- ガウス消去法（直接法）
- ガウス・ジョルダン法（直接法）
- ヤコビ法（反復法）
- ガウス・ザイデル法（反復法）
- SOR法（反復法）
などがあります。
詳しく勉強したい方は、以下の参考書がとてもわかりやすいです。
数値計算の闇について詳しく知りたい方は、☟こちらの参考書も合わせてお読みください。
Follow @t_kun_kamakiri