こんにちは(@t_kun_kamakiri)。
こちらにある英語で書かれたPython流体の数値計算シリーズを日本語でまとめあげました！
この記事ではこんな人を対象にしています。
- Pythonを使い始めたけどどう使うかわからない
- 流体の数値計算をはじめて勉強する人
最終的には、以下のような数値計算を実装しています！
【最終課題１】「キャビティ流れ」と呼ばれる流れ。【最終課題２】
「ポアズイユ流れ」と呼ばれる流れ。
最後まで読めば、きっとこうなっていることでしょう(‘ω’)ノ
正直言って、流体力学、さらには流体解析や流体の数値シミュレーションはそんなに易しいものではありません！
これを書いている僕は「流体解析なんもわからん(´Д｀)」という人です。
そんな初心者だからこそ、いちから自分の言葉で書いてみることに意味はあると考えて書いてみました。
英語で書かれたこちらの翻訳ではなく、自分の言葉で解釈をし直して書いています。
「Python・流体・流体の数値計算」のいずれかの初学者にはおすすめできる内容かと思います(^^)/
Python流体の数値計算シリーズ
Pythonを使って流体の数値計算の基礎を学ぶことができます。
- 【第1回Python流体の数値計算】目標と環境構築。まずはここからはじめよう！
- 【第2回Python流体の数値計算】Numpyの使い方を確認する。
- 【第3回Python流体の数値計算】「参照渡し」と「値渡し」の違いを理解する。
- 【第4回Python流体の数値計算】１次元移流方程式を差分法で実装する。
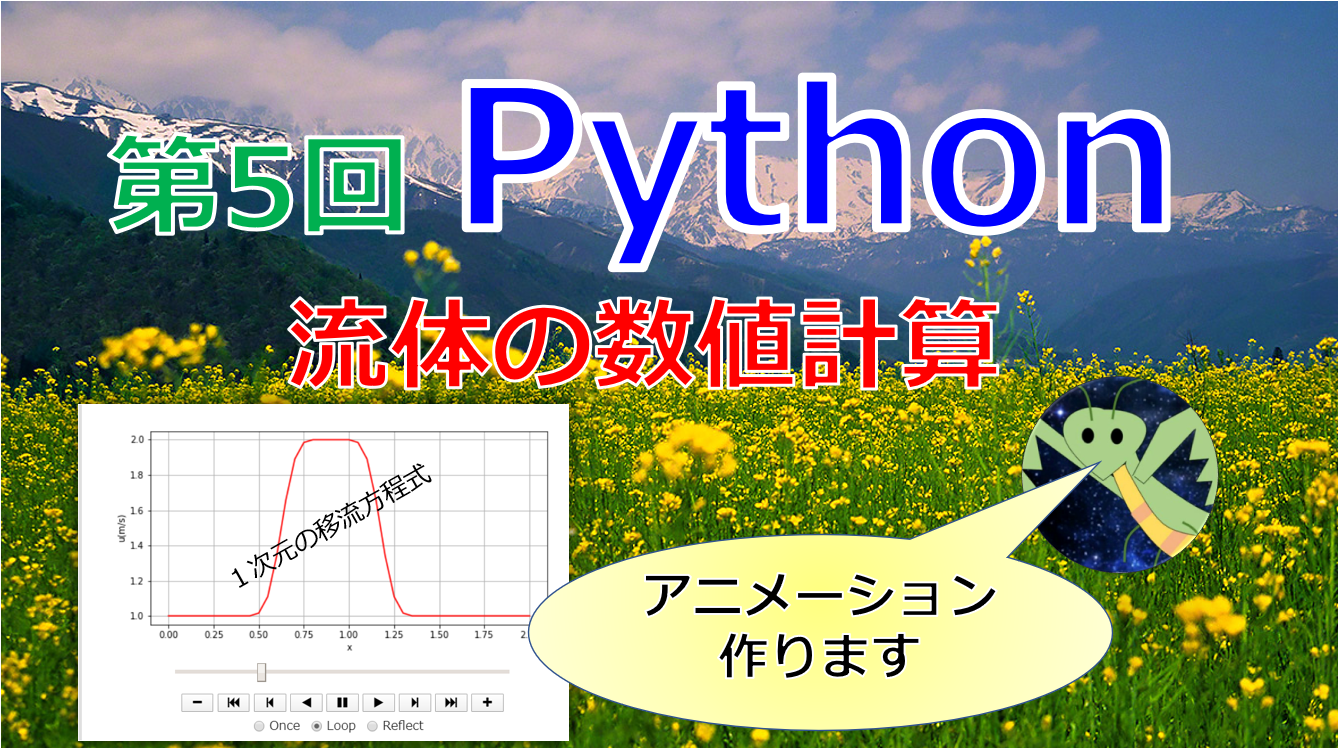
- 【第5回Python流体の数値計算】移流方程式をGoogle Colaboratoryでアニメーション作成。
- 【第6回Python流体の数値計算】移流方程式のクーラン条件！数値的安定性（差分法）
- 【第7回Python流体の数値計算】１次元拡散方程式を差分法で実装する。
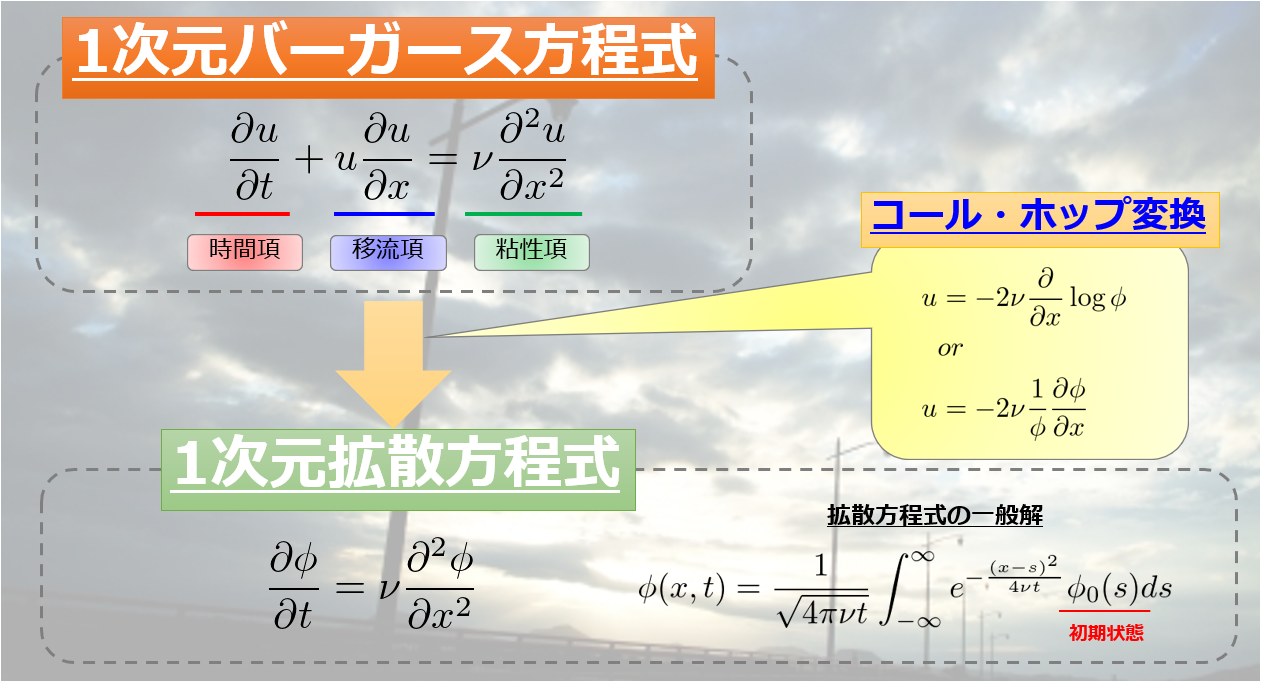
- 【第8.1回Python流体の数値計算】バーガース方程式を差分法で実装する。
【第8.2回Python流体の数値計算】バーガース方程式の非線形項は異なる波数間での相互作用が生じるという意味。
【第8.3回Python流体の数値計算】バーガース方程式の一般解（コール・ホップ変換によって拡散方程式になる） - 【第9回Python流体の数値計算】Numpyでスライスを使って計算を速くする！
- 【第10回Python流体の数値計算】2次元の線形移流方程式をGoogle Colaboでアニメーション作成する。
- 【第11回Python流体の数値計算】2次元移流方程式をGoogle Colabでアニメーション作成する。
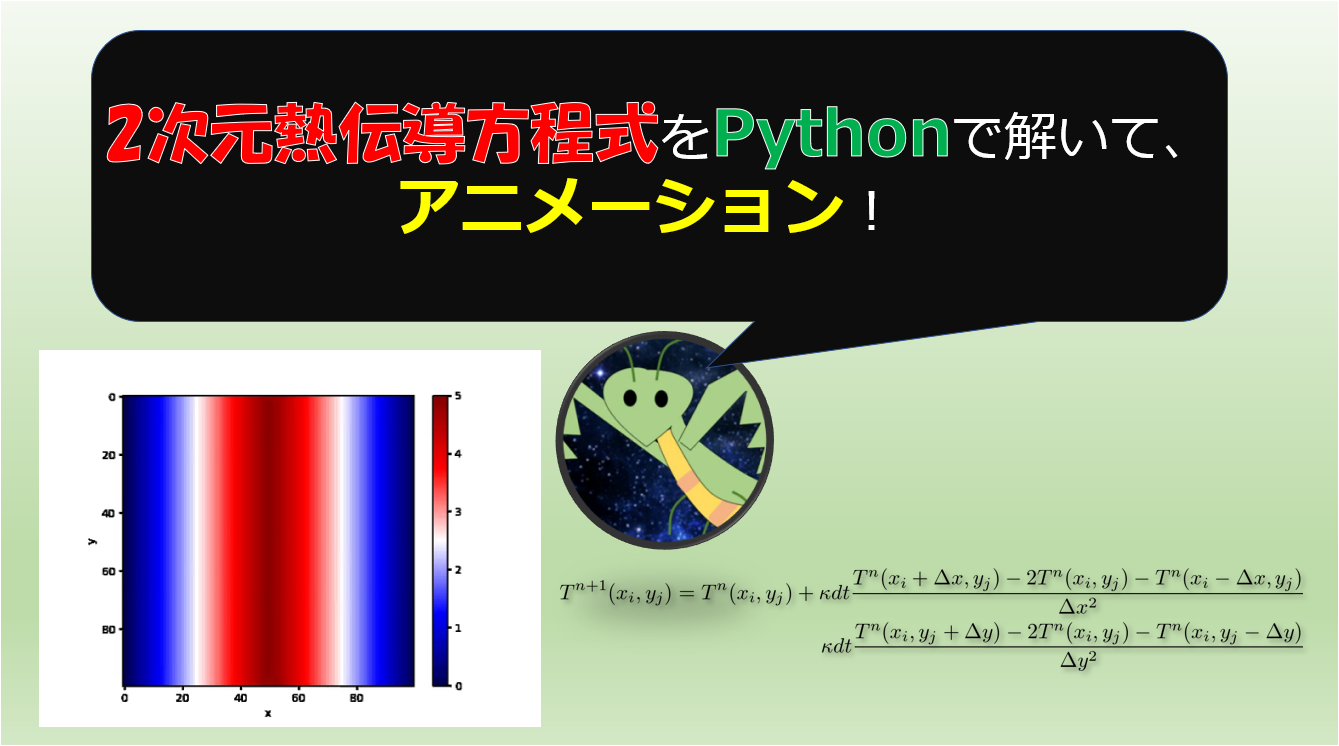
- 【第12回Python流体の数値計算】2次元拡散方程式をGoogle Colabでアニメーション作成する。
- 【第13回Python流体の数値計算】2次元バーガース方程式をGoogle Colabでアニメーション作成する。
- 【第14回Python流体の数値計算】2次元ラプラス方程式をPythonで実装する。
- 【第15回Python流体の数値計算】2次元ポアソン方程式をPythonで実装する。
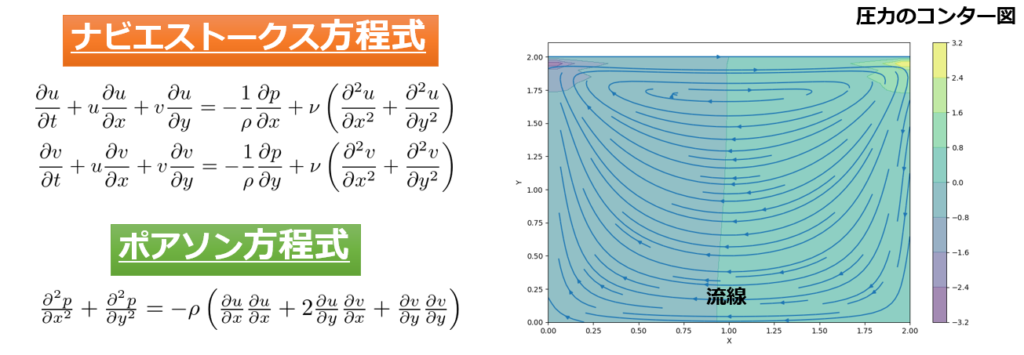
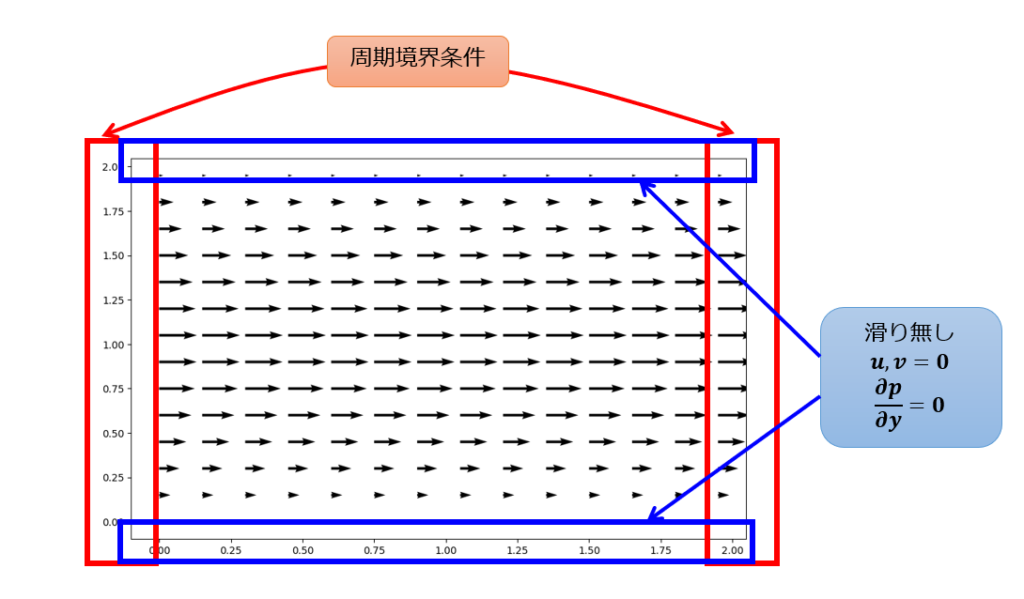
- 【第16回Python流体の数値計算】2次元ナビエストークス方程式！キャビティ流れをPythonで実装する。
- 【第17回Python流体の数値計算】2次元ナビエストークス方程式！ポアズイユ流れをPythonで実装する。
本シリーズで学んだことを活かして、境界条件や空間領域などの設定を変更しながら流体の数値計算を楽しんでもらえればと思います♪
また、もう少し詳しく解説してほしいなどのリクエストがありましたが、記事として追加したいと思いますので遠慮なくお申し付けください。
また、ブログ記事に関係ない内容など個別に教えてほしいという方は「物理の質問サービス（有料）」もやっていますので、是非よろしお願いします。
※ブログ内の記事に関する質問は無料ですので、記事一番下の「コメント欄」もしくは「お問い合わせフォーム」までご連絡いただければ幸いですm(__)m
おすすめの書籍紹介
本シリーズで紹介したのは流体の数値計算のほんの一部の解き方だけです。
取り扱う流体現象や方程式によっては十分な精度がでなかったり、安定的に解いてくれなかったりします。
流体の数値計算を行う際は、以下の内容をきちんと学んでおく必要があります。
- プログラミング言語（Pythonなど）
- 流体力学
- 数値流体
- 数値計算
以下に、書籍の紹介をしておきます。
ネット上には無料で多くのことが学べるのですが、ネット情報だけだと情報が偏ったりします。
やっぱり書籍を手に取って体系だって学んだ方が良い場合も多いです。
初心者でもので体系だって学ぶことができる、且つあまり難しすぎない書籍をここで紹介しておきます。
Pythonの完全初心者は書籍で学ぶとよい
Python自体が不安だという方は、こちらの書籍から勉強しても良いかも知れません。
☟こちらの本がPython初心者が挫折することなく勉強できる本です。
（本記事のようのPython使用環境と異なりますが、とてもわかりやすいので全く問題ありません）
流体の勉強をしたい方
流体の数値計算以前に、流体力学を勉強しないと！！って思っている方は以下の参考書からはじめてみるのが良いと思います。
工学よりに書かれていて実用的な内容も触れながら、流体の理論的な内容も易しく書かれていますので大学１年生で偏微分を学んだ方にとってはちょうどよい参考書です。
数値流体の書籍
本記事で紹介している数値計算手法は、多くの数値解法のごく一部です。
特に、非線形方程式で記述できる流体現象のようなものは注意深く数値解法を選択しなくてはいけません。
以下の書籍は、値段が高いですが有限体積法をメインに数値解法がとても詳しく解説されています。
数値計算の書籍
今回紹介したポアソン方程式は「ヤコビ法」と呼ばれる反復計算を行っていますが、その他の有名な数値的解法のをいくつか挙げておきます。
- ガウス消去法（直接法）
- ガウス・ジョルダン法（直接法）
- ヤコビ法（反復法）
- ガウス・ザイデル法（反復法）
- SOR法（反復法）
などがあります。
詳しく勉強したい方は、以下の参考書がとてもわかりやすいです。
数値計算の闇について詳しく知りたい方は、☟こちらの参考書も合わせてお読みください。
Follow @t_kun_kamakiri
