流体力学「5つの独立な物理量」と「5つの独立な基礎方程式」

流体力学を学んでいったい何を知りたいのか？

・・・・そんなことを思ったことはありませんか？

カマキリ

僕はそう思った

何を知れれば流体力学という学問の恩恵を受けれるでしょう・・・・

ざっくりと・・・・流れの様子を知りたい！！！

これが思いのたけです。

カマキリ

流れの様子ってなんだ！？？

カマキリ

こんな流れをシミュレーションで再現したら良いのか？

ん～、なんか大雑把！

やはり、物理現象を扱っているのですから、ある時刻、ある位置に対する物理量を知ることが流体力学でも求められることですよね。

本記事の内容

流体の運動を記述する物理量について解説する

というわけで、流体の運動を記述する物理量ってなんでしょう？というのが本記事の内容です。

流体力学における物理量
熱力学的に独立な物理量は2つだけ
流体力学のおける物理量は5つ
流体力学における5つの独立な方程式
まとめ
参考文献

流体力学における物理量

流れを知りたいと思ったときに、どういった物理量を知りたいですかね？

流速\(v_{x},v_{y},v_{z}\)
圧力\(p\)
温度\(T\)
密度\(\rho\)
（内部エネルギー\(E\)）
（エントロピー\(S\)）

こんなところでしょうね。

運動学的な量：流体現象なので、流体の速度（3成分）

その他、熱力学的な量：圧力、温度、密度、内部エネルギー、エントロピー・・・

なども知りたいですね。

基本的に、知りたい物理量（未知数）が\(n\)個あれば、独立な方程式が\(n\)個なければすべての未知数を求めることができません。

上に挙げた物理量だけでも、8個もあるぞ！！ってことですが、ご安心あれ！

赤色で書いた量は熱力学的な物理量においては、互いに独立な量は２つだけなのです。

熱力学的に独立な物理量は2つだけ

熱力学的な量：圧力、温度、密度、内部エネルギー、エントロピー・・・

などは実は互いに独立ではなく、状態方程式などを介して、本当に独立な変数は2つだけになります。

熱力学の状態方程式

\begin{align*}f(P,T,\rho)=0\end{align*}

最もわかりやすい例が、理想気体の状態方程式\(p=\rho RT\)です。

これを見れば、

未知数：3つ
式：１つ

なので、自由は3-1=2となるので、独立な変数を2つ決めればあとは芋づる式にわかるというわけです。

流体力学のおける物理量は5つ

今までの話をまとめると・・・

流体における物理量は以下の5つになるということです。

運動学的な物理量：流速\(v_{x},v_{y},v_{z}\)（3成分）
熱力学的な物理量を2つ

そうすると、「未知数：5つ」となるため、全ての物理量を決定するためには、5つの独立な方程式を用意する必要があります。

流体力学における5つの独立な方程式

流体力学における5つの独立な方程式を以下にまとめておきましょう！

質量保存則

\begin{align*}\frac {\partial \rho }{\partial t}+\frac{\partial \rho v_{j}}{\partial x_{j}}=0\cdot\cdot\cdot (1)\end{align*}

「質量保存則」の記事はこちら

流体力学質量保存則（連続の式）の導出

これで1つ目！！

運動量保存則

\begin{align*}\frac{\partial \rho v_{i}}{\partial t}+\frac{\partial\rho v_{i}v_{j}}{\partial x_{j}}=\frac{\partial \sigma_{ij}}{\partial x_{j}}+\rho K_{i}\cdot\cdot\cdot (2)\end{align*}

「運動量保存則」の記事はこちら

流体力学運動量保存則の導出

これで4つ目！！

※運動量保存則は3成分なので、合計3つの式があります。

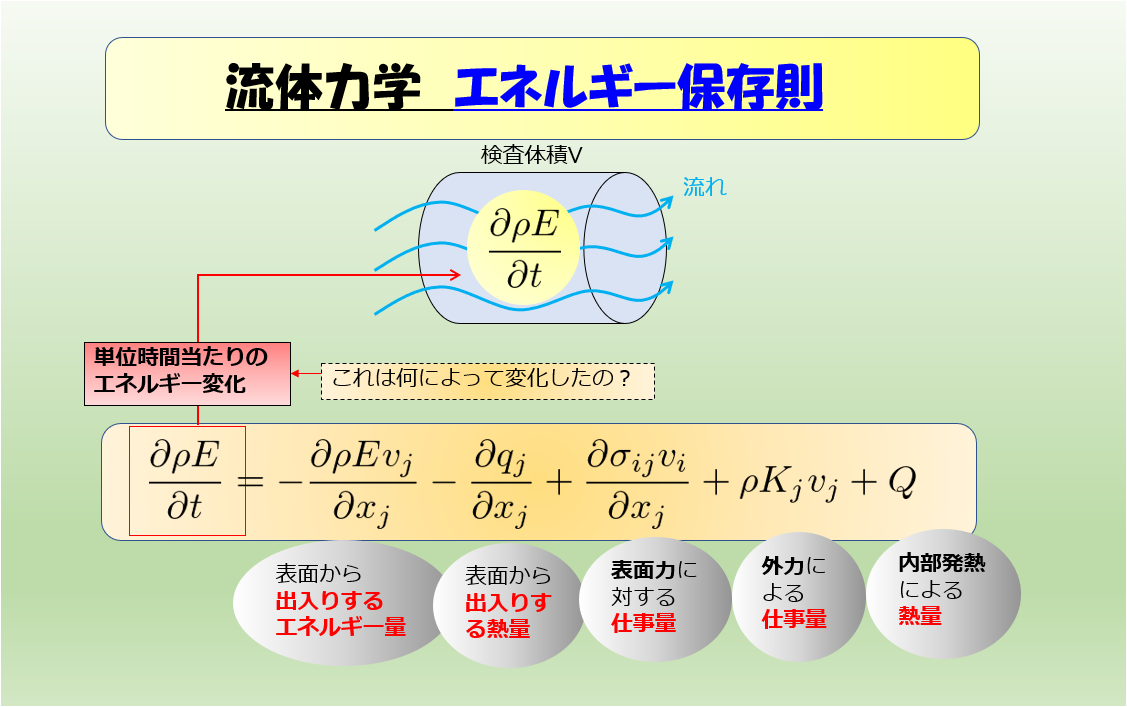
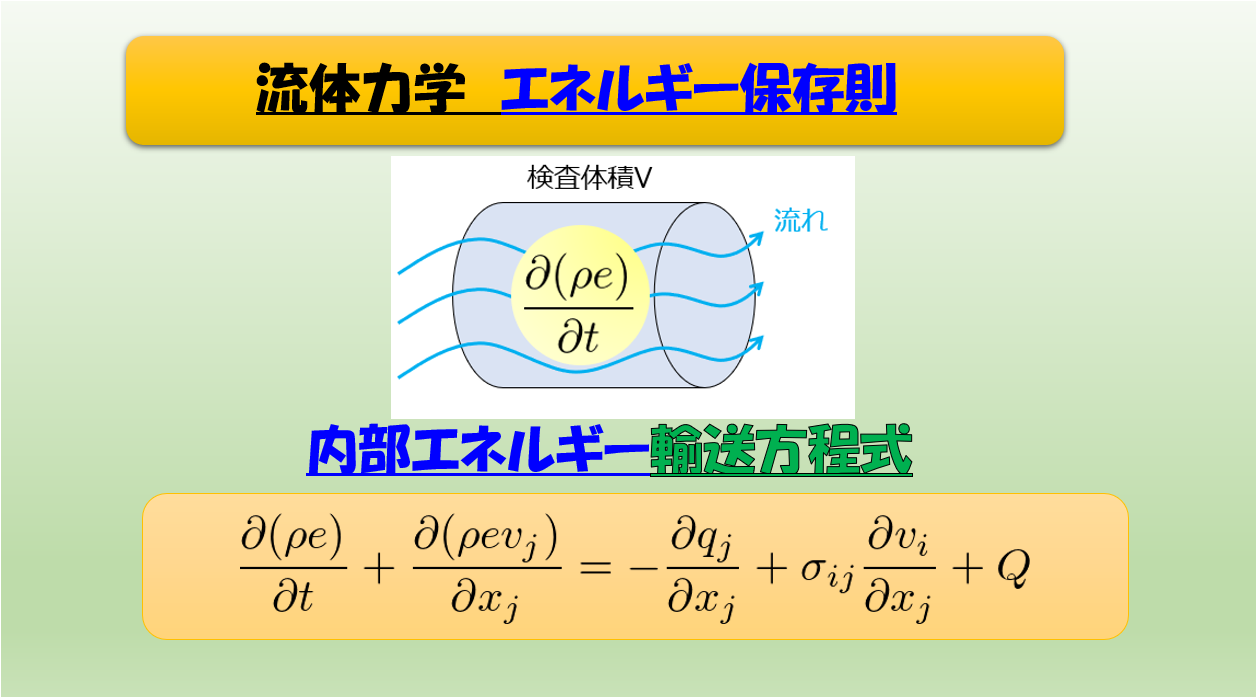
エネルギーの保存則

\begin{align*}\frac{\partial \rho E}{\partial t}+\frac{\partial \rho E v_{j}}{\partial x_{j}}=-\frac{\partial q_{j}}{\partial x_{j}}+\frac{\partial \sigma_{ij}v_{i}}{\partial x_{j}}+\rho K_{j}v_{j}+Q\cdot\cdot\cdot (3)\end{align*}

\(E=e+\frac{1}{2}\boldsymbol{v}^2\)
e：内部エネルギー

「エネルギー保存則」の記事はこちら

流体力学エネルギー保存則の導出

これで5つ目！！

つまり、上記の(1)~(3)式の保存則が独立な5つの方程式になります。