【解析力学】ラグランジュ形式とハミルトン形式の違いを理解しておこう。

解析力学を学習すると、ラグランジュ形式とハミルトン形式という２つの記述の方法を学びますよね。

本記事では、
ラグランジュ形式、ハミルトン形式についてまとめる。

復習：解析力学とは
1. 力学の場合
  - 例１：質点の運動（位置を求める場合）
  - 例２：振り子運動（位置ではなく角度をもとめる場合）
ラグランジュ形式
ハミルトン形式
まとめ
参考図書

復習：解析力学とは

解析力学は、ニュートン力学をより美しく一般的な形式に従って運動を記述できるようにした学問である。

詳しくはこちらの記事をお読みいただきたいです。

https://takun-physics.net/?p=177

力学の場合

運動状態を決定しようとした場合、初期状態を与えて運動方程式\(ma=F\)に代入すれば、時刻\(t\)における運動が決定できますよね。

運動状態が決定されるとは、具体的にはどういう意味であるかというと、「ある時刻における位置と速度が求まる」ということです。

力学における目標は、運動方程式を解いて「ある時刻における位置と速度を求めること」です。

この目標は解析力学でも同じです。

しかし、広い意味で力学的な運動状態を決定しようとした場合、以下で示すように位置は必ずしも位置でなくてもよいことがわかります。

具体例を２つ見てみましょう。

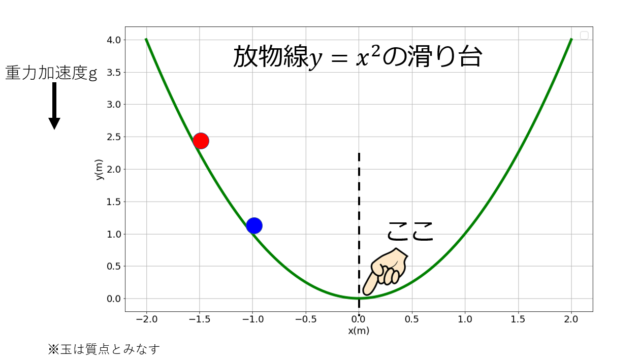
例１：質点の運動（位置を求める場合）

「時刻\(t=0\)」において、下の絵のように質点を投げたとき、時刻\(t\)における位置と速度を求めなさい」という問題があったとします。

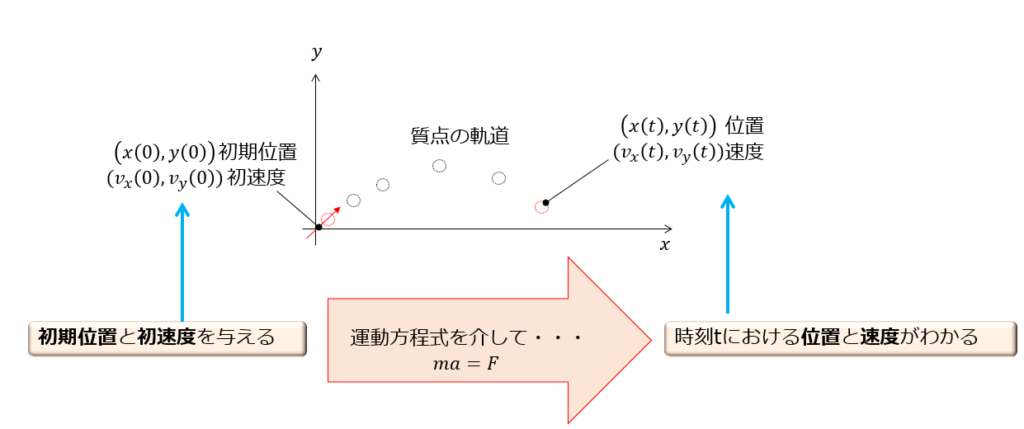
運動方程式は、

\begin{align*}m\frac{d^{2}x}{dt^{2}}=F_{x}\end{align*}

\begin{align*}m\frac{d^{2}y}{dt^{2}}=F_{y}\end{align*}

です。

初期状態が与えられているので、(1)(2)の運動方程式を解くことにより、位置と速度を求めることができます。

例２：振り子運動（位置ではなく角度をもとめる場合）

以下のような振り子運動において、ある時刻における運動状態を知りたい場合、必ずしも位置を求める必要がないことがわかります。

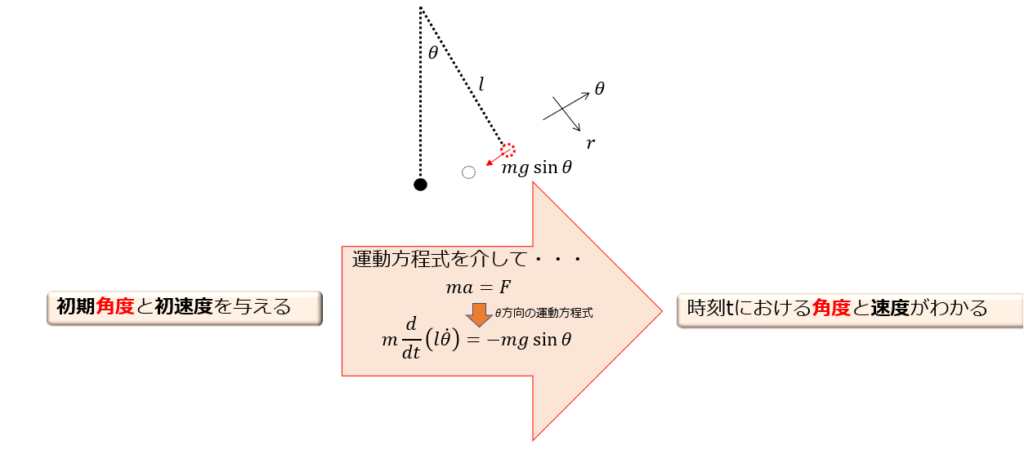
\(\theta\)方向の運動方程式は、

\begin{align*}m\frac{d}{dt}(l\dot{\theta})=-mg\sin\theta\cdot\cdot\cdot (1)\end{align*}

です。

ここで、\(\theta \simeq 0\)とすると、\(\sin\theta\simeq \theta\)であるから(3)式は、

\begin{align*}m\frac{d}{dt}(l\dot{\theta})=-mg\theta\cdot\cdot\cdot (4)\end{align*}

となり、\(\theta\)を求める運動方程式になっています。

もちろん\(\theta\)を求めることができれば、位置座標\(x,y\)は求めることができます。

つまり、力学的な運動状態は広い意味ではある変数（一般座標）、その微分（一般速度）を指定するということになります。

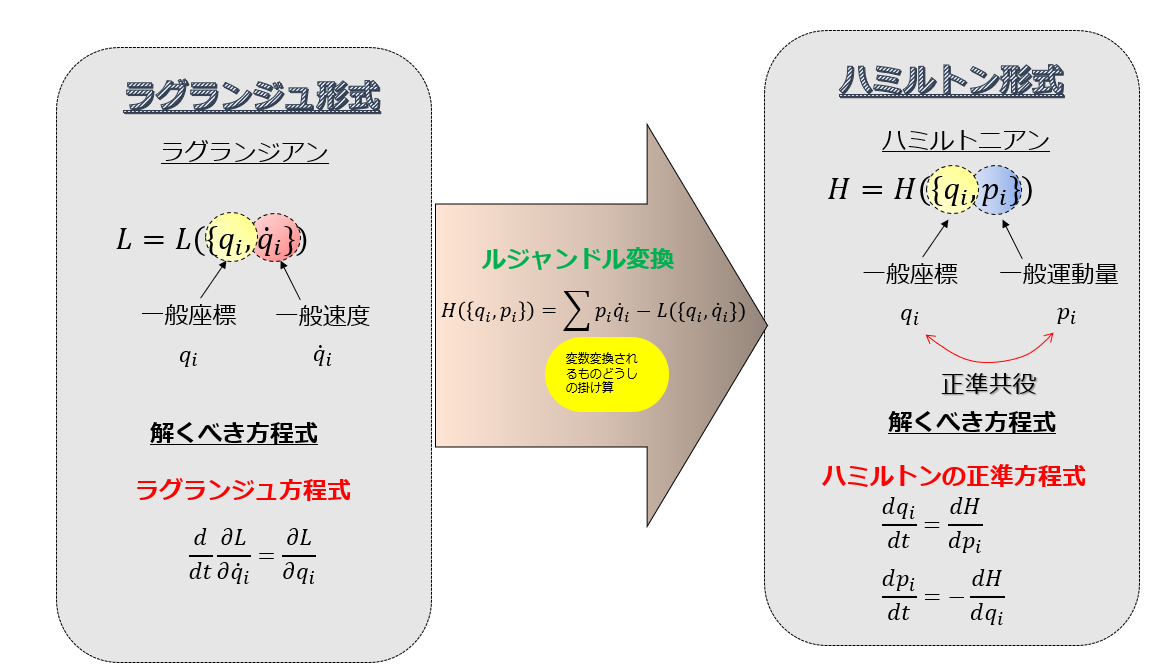
ラグランジュ形式

ラグランジュ形式は・・・・

まず、力学的な状態を一般座標\(q_{i}\)と一般速度\(\dot{q}_{i}\)を変数として、ラグランジアン\(L(\{q_{i},\dot{q}_{i}\})\)を作ります。

\begin{align*}L=L(\{q_{i},\dot{q}_{i}\})\cdot\cdot\cdot (5)\end{align*}

※表記：\(L(\{q_{i},\dot{q}_{i}\})=L(\{q_{1},q_{2},\cdot\cdot\cdot,q_{f},\dot{q}_{1},\dot{q}_{2},\cdot\cdot\cdot,\dot{q}_{f}\})\)

\(\{q_{i},\dot{q}_{i}\}\)の組が\(f\)個ある場合は、\(f\)自由度となります。

このように、実現しうる力学的な運動状態を一般座標\(q_{i}\)と一般速度\(\dot{q}_{i}\)を変数として記述したものをラグランジュ形式と呼びます。

https://takun-physics.net/?p=283

↑この記事にも書きましたが、

座標系がデカルト座標だろうが、極座標だろうが、座標を一般座標\(q_{i}\)とその時間微分である一般速度\(\dot{q}_{i}\)を変数とするとき、最小作用の原理より、

ラグランジュ方程式：

\begin{align*}\frac{d}{dt}\frac{\partial L}{\partial \dot{q}_{i}}=\frac{\partial L}{\partial q_{i}}\cdot\cdot\cdot (6)\end{align*}

が求まります。

ラグランジュ方程式(6)を用いれば、初期状態\(\{q_{i}(0),\dot{q}_{i}(0)\}\)がわかれば時刻\(t\)での\(\{q_{i}(t),\dot{q}_{i}(t)\}\)がもとまるので運動状態が決定されるというわけですね。

ハミルトン形式

ラグランジアン形式は・・・・一般座標\(q_{i}\)と一般速度\(\dot{q}_{i}\)を変数としていたのに対して、

ハミルトン形式は、一般座標\(q_{i}\)と一般運動量\(p_{i}\)を変数とし、ある関数ハミルトニアンによって運動が決定されます。

\begin{align*}H=H(\{q_{i},p_{i}\})\cdot\cdot\cdot (7)\end{align*}

※ハミルトニアンは全エネルギーを表しています。

変数の組を、

\begin{align*}\{q_{i},\dot{q}_{i}\}⇒\{q_{i},p_{i}\}\cdot\cdot\cdot (8)\end{align*}

とするわけですね。

(8)のような変数変換はルジャンドル変換により行われます。

ルジャンドル変換

\(H(\{q_{i}\},\{p_{i}\})=\sum_{i}p_{i}\dot{q_{i}}-L(\{q_{i}\},\{\dot{q_{i}}\})\)

※一般運動量：\(p_{i}=\frac{\partial L}{\partial \dot{q_{i}}}\)

ルジャンドル変換しらねーって方は↓こちらをお読みください(^^)v

ルジャンドル変換の記事はこちら

このように、実現しうる力学的な運動状態を一般座標\(q_{i}\)と一般運動量\(p_{i}\)を変数として記述したものをハミルトン形式と呼びます。

そして、ラグランジアン\(L\)のときはラグランジュ方程式を解けば力学的な状態を求めることができたように、ハミルトン形式の場合はハミルトンの正準方程式を解けば、力学的な状態を決定することができます。

ハミルトンの正準方程式：

\begin{align*}\frac{dq_{i}}{dt}=\frac{\partial H}{\partial p_{i}}\cdot\cdot\cdot (9)\end{align*}

\begin{align*}\frac{dp_{i}}{dt}=-\frac{\partial H}{\partial q_{i}}\cdot\cdot\cdot (10)\end{align*}

まとめ

ラグランジュ形式
変数：一般座標\(q_{i}\)と一般速度\(\dot{q}_{i}\)

ラグランジュ方程式：

\begin{align*}\frac{d}{dt}\frac{\partial L}{\partial \dot{q}_{i}}=\frac{\partial L}{\partial q_{i}}\cdot\cdot\cdot (6)\end{align*}

ハミルトン形式
変数：一般座標\(q_{i}\)と一般速度\(p_{i}\)

ハミルトンの正準方程式：

\begin{align*}\frac{dq_{i}}{dt}=\frac{\partial H}{\partial p_{i}}\cdot\cdot\cdot (9)\end{align*}

\begin{align*}\frac{dp_{i}}{dt}=-\frac{\partial H}{\partial q_{i}}\cdot\cdot\cdot (10)\end{align*}