大学数学

【演習問題（ギブスの現象）】矩形波のフーリエ級数展開

こんにちは(@t_kun_kamakiri)。

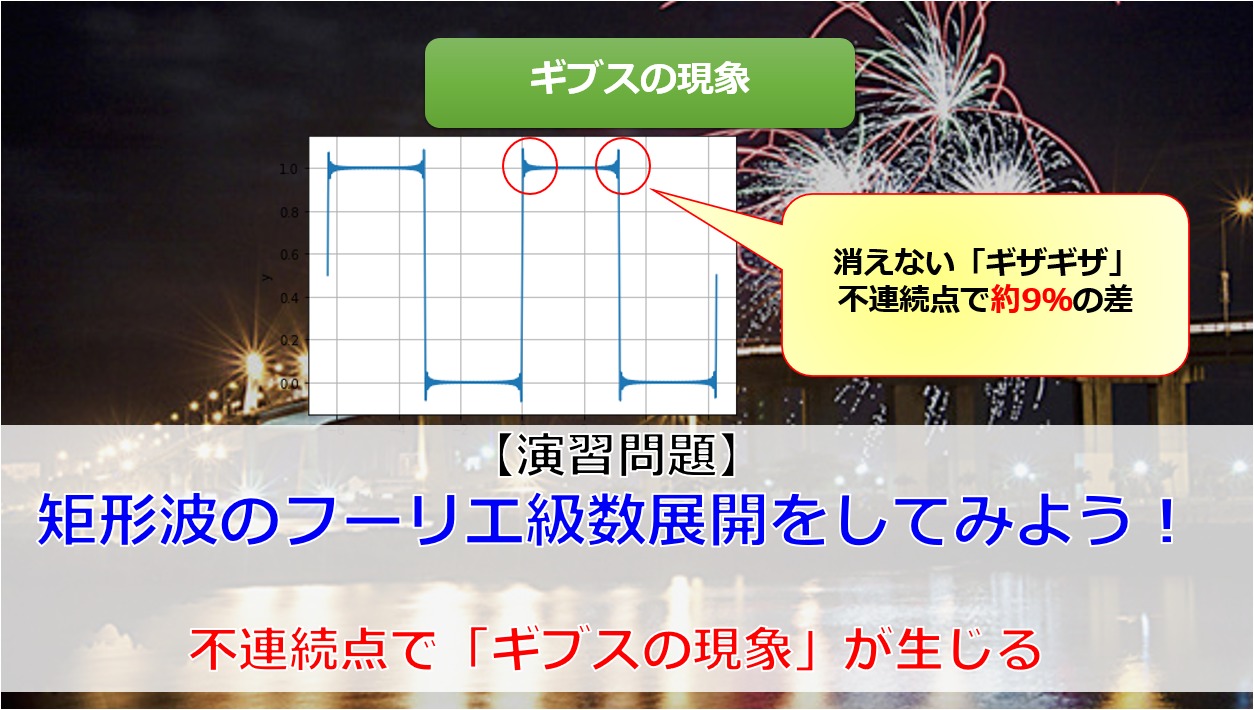
先日に「不連続な関数をフーリエ級数展開したら、ギブスの現象が出るよ」というのをツイートすると、いいねをしてくれる人が多かったので、記事にしてみようと思います。
※アニメーションにもしてみました。

こういう不思議な現象って皆さん好きですよね。

フーリエ級数展開は、とても有名なので記事にしておきました。

フーリエ級数展開の記事はこちら

 

よく誤解があるのは、「何でもかんでも一般的な周期関数はフーリエ級数展開できる」という誤解です。

カマキリ

本当に何でもかんでも一般的な周期関数はフーリエ級数展開できるのかというものですよね。

フーリエ級数展開については、以下に簡単にまとめておきます。

\(x\)の範囲を[\(-L\leq x\leq L\)]とし、関数の集合を、
\begin{align*}\{1,\sin k_{1}x,\sin k_{2}x,\cdot\cdot\cdot\sin k_{n}x,\cdot\cdot\cdot,\cos k_{1}x,\cos k_{2}x,\cdot\cdot\cdot\cos k_{n}x,\cdot\cdot\cdot \}\end{align*}

※\(k_{n}=\frac{n\pi}{L}\)
とするとき、任意関数\(f(x)\)は
\begin{align*}f(x)  = \frac{a_{0}}{2}+\sum^{\infty}_{n=1}a_{n}\sin k_{n}x+\sum^{\infty}_{n=1}b_{n}\cos k_{n}x\tag{1}\end{align*}

と書けるよという話があります。
この（1）がフーリエ級数展開と呼ばれています。
※サイン・コサインは\(2L\)周期関数ですので、任意関数\(f(x)\)も同じ\(2L\)周期関数に限った話であることに注意しましょう。

見てわかる通り、フーリエ級数展開は「連続かつ滑らかな関数である\(\sin, \cos\)の無限級数」で記述しています。

だったら\(f(x)\)が途中で不連続になっていたら一体どうなるのか？

そこで、本記事の主題は、

本記事の内容はこちら

「不連続な関数\(f(x)\)をフーリエ級数展開したら、ギブスの現象が出るよ」です！

 

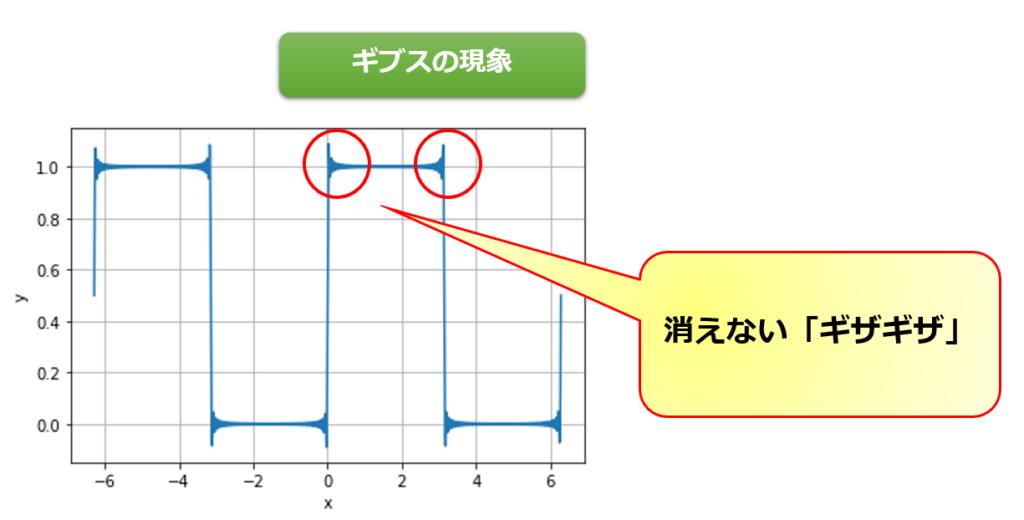
不連続点以外はフーリエ級数展開できそうですが、不連続点ではどれだけ和をとっても消えないギザギザが生じます。
つまり、どれだけフーリエ級数展開の和を足しても、元の関数\(f(x)\)にならないというのが本記事の主題でもあります。

実際に演習問題を解きながら、

  1. 矩形波のフーリエ級数展開を行う
  2. フーリエ級数展開した関数は不連続点で元の関数との差は何％か？

というのを見ていきます。

スポンサーリンク

目次
  1. 【矩形波（くけいは）】不連続な関数とは
  2. 【演習問題】矩形波をフーリエ級数展開する
  3. フーリエ級数展開の振る舞いを調べる
  4. 不連続点での差（何％のズレがあるのか？）
  5. まとめ

【矩形波（くけいは）】不連続な関数とは

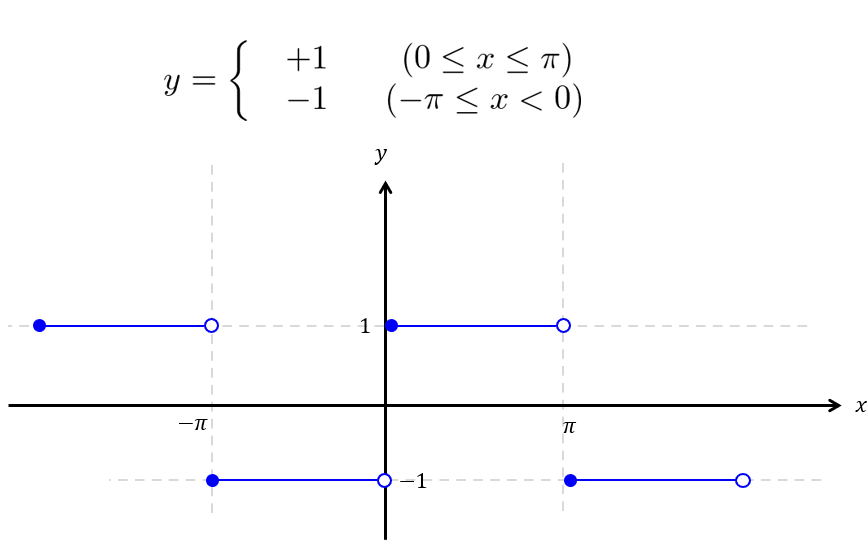
難しい話はさておき、以下の不連続な関数を考えてみましょう。

カマキリ

↓こんなんだったり

【例1】

カマキリ

↓こんなんだったり

【例2】

こういった一定値をとるような波形を矩形波（くけいは）と呼びます。

「矩形（くけい）」と読みます。

この矩形波をフーリエ級数展開で、

\begin{align*}f(x)  = \frac{a_{0}}{2}+\sum^{\infty}_{n=1}a_{n}\sin k_{n}x+\sum^{\infty}_{n=1}b_{n}\cos k_{n}x\tag{1}\end{align*}

このように本当に展開できるのかという疑問です。

例えば、\(m\rightarrow \infty\)のときに。

\begin{align*}
|f(x)- \frac{a_{0}}{2}+\sum^{m}_{n=1}a_{n}\sin k_{n}x+\sum^{m}_{n=1}b_{n}\cos k_{n}x|\rightarrow 0\tag{2}
\end{align*}

と収束してくれれば良いのですが、そうなるかどうかはわかりません。
※正確には数学的には知られていますが、何も考えなかったらわからないですよね。

難しい話を置いといて、とりあえず関数\(f(x)\)の不連続点でギブスの現象と呼ばれるギザギザが出るよということです。

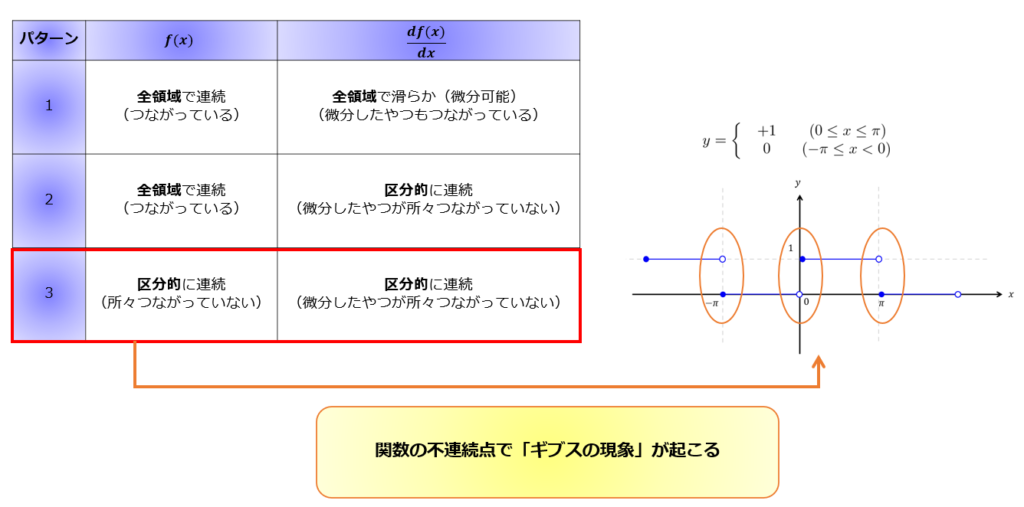
このあたりの話をすると数学の込み入った話になるので別途話します。

実際に計算の儀式に従ってフーリエ級数展開をすることができるので、とりあえず何も考えずにフーリエ級数展開してみましょう(^^)/

【演習問題】矩形波をフーリエ級数展開する

今回考えるのは以下の矩形波とします。
※【例2】の方がじゃっかん難しかったりするため。

【演習問題】
上記の矩形波をフーリエ級数展開してみましょう！！

カマキリ

手を動かして計算してみましょう。

【以下、解説】

では、さっそく始めます。

一般的な\(f(x)\)のフーリエ級数展開は、

\begin{align*}f(x)  = \frac{a_{0}}{2}+\sum^{\infty}_{n=1}a_{n}\sin k_{n}x+\sum^{\infty}_{n=1}b_{n}\cos k_{n}x\tag{1}\end{align*}

と書けます。

後は、フーリエ係数である\(a_{n}\)を求めれば良いです。

それには以下の予備知識が必要です。

\begin{align*}
\int^{\pi}_{-\pi}\sin mx\sin nx dx=\pi\delta_{mn}
\end{align*}

\begin{align*}
\int^{\pi}_{-\pi}\sin mx\cos nx dx=0
\end{align*}

\begin{align*}
\int^{\pi}_{-\pi}\cos mx\cos nx dx=\pi\delta_{mn}
\end{align*}

※クロネッカーデルタ\(\delta_{mn}\)は、「\(m=n\)のときは1」「\(m\neq n\)のときは0」

■両辺から\(\sin mx\)をかけて、\(x\)で積分することで、\(a_{n}\)を求めることができます。

\begin{align*}
\int^{\pi}_{-\pi}f(x)\sin mx\,dx=\int^{\pi}_{-\pi}\bigg(\frac{a_{0}}{2}+\sum_{n=1}^{\infty}a_{n}\sin nx+\sum_{n=1}^{\infty}b_{n}\cos nx\bigg)\sin mx\,dx\tag{3}
\end{align*}

左辺と右辺をそれぞれ求めます。

\begin{align*}
(右辺)&=\int^{\pi}_{-\pi}\bigg(\frac{a_{0}}{2}+\sum_{n=1}^{\infty}a_{n}\sin nx+\sum_{n=1}^{\infty}b_{n}\cos nx\bigg)\sin mx\,dx\\
&=\int^{\pi}_{-\pi}\frac{a_{0}}{2}\sin mx \,dx+\int^{\pi}_{-\pi}\sum_{n=1}^{\infty}a_{n}\sin nx \sin mx \,dx+\int^{\pi}_{-\pi}\sum_{n=1}^{\infty}b_{n}\cos nx\sin mx\, dx\\
&=\pi a_{n}\tag{4}
\end{align*}

この積分は、\(n=m\)のときしか残らないため、\(a_{n}\)のみが残ります。

\begin{align*}
(左辺)&=\int^{\pi}_{-\pi}f(x)\sin mx\,dx\\
&=\int^{0}_{-\pi}0\times \sin mx\,dx+\int^{\pi}_{0}\sin mx\,dx\\
&=\left [ \frac{-1}{m}\cos mx \right ]^{\pi}_{0}\\
&=\frac{1-\cos m\pi}{m}\\\
&=\frac{1-(-1)^m}{m}\tag{5}
\end{align*}

\(\cos m\pi=(-1)^m\)としました。
※\(m\)の値によって、\(-1,1\)を繰り返すため。

これより、\(m=n\)なので、

\begin{align*}
a_{n}=\frac{1-(-1)^n}{\pi n}
\end{align*}

\(a_{n}\)が求まりました。

■\(x\)で積分することで、\(a_{0}\)を求めることができます。

\begin{align*}
\int^{\pi}_{-\pi}f(x)\,dx=\int^{\pi}_{-\pi}\bigg(\frac{a_{0}}{2}+\sum_{n=1}^{\infty}a_{n}\sin nx+\sum_{n=1}^{\infty}b_{n}\cos nx\bigg)\,dx\tag{6}
\end{align*}

左辺と右辺をそれぞれ求めます。

\begin{align*}
(右辺)&=\int^{\pi}_{-\pi}f(x)\,dx\\
&=2\pi\tag{7}
\end{align*}

右辺の計算は、第二項と第三項は残らないため、

\begin{align*}
(右辺)&=\int^{\pi}_{-\pi}\sum_{n=1}^{\infty}a_{n}\frac{a_{0}}{2}\,dx\\
&=\pi a_{0}\tag{8}
\end{align*}

よって、フーリエ係数\(a_{n}\)は\(n=m\)なので、

\begin{align*}
a_{0}=\frac{1}{2}\tag{9}
\end{align*}

■両辺から\(\cos mx\)をかけて\(x\)で積分することで、\(b_{n}\)を求めることができます。

\begin{align*}
\int^{\pi}_{-\pi}f(x)\cos mx\,dx=\int^{\pi}_{-\pi}\bigg(\frac{a_{0}}{2}+\sum_{n=1}^{\infty}a_{n}\sin nx+\sum_{n=1}^{\infty}b_{n}\cos nx\bigg)\cos mx\,dx\tag{10}
\end{align*}

左辺と右辺をそれぞれ求めます。

\begin{align*}
(左辺)&=\int^{\pi}_{-\pi}f(x)\cos mx\,dx\\
&=\int^{0}_{-\pi}0\times \cos mx\,dx+\int^{\pi}_{0}\cos mx\,dx\\
&=\left [ \frac{1}{m}\sin mx \right ]^{\pi}_{0}\\
&=0\tag{11}
\end{align*}

右辺の計算は、第一項と第二項を積分すると0になります。

計算するべきは第三項だけです。

\begin{align*}
(右辺)&=\int^{\pi}_{-\pi}\bigg(\frac{a_{0}}{2}+\sum_{n=1}^{\infty}a_{n}\sin nx+\sum_{n=1}^{\infty}b_{n}\cos nx\bigg)\cos mx\,dx\\
&=\pi b_{n}\tag{12}
\end{align*}

なので、

\begin{align*}
b_{n}=0\tag{13}
\end{align*}

となります。

よって、\(f(x)\)のフーリエ級数展開は、

\begin{align*}
f(x)=\frac{1}{2}+\sum_{n=1}^{\infty}\frac{1-(-1)^n}{\pi n}\sin nx\tag{14}
\end{align*}

これにより、演習問題の解答が終わりました(^^)/

フーリエ級数展開の振る舞いを調べる

(14)をイコールで結んでよいのかはわからないですよね。
ということで、フーリエ級数展開した結果だということで、区別するために添え字をつけておきましょう。

\begin{align*}
f_F (x)=\frac{1}{2}+\sum_{n=1}^{\infty}\frac{1-(-1)^n}{\pi n}\sin nx\tag{14.1}
\end{align*}

※フーリエ(Fourier)の「F」を添え字にしました。

本当に、\(f_F(x)\)をフーリエ級数展開(14)の形で記述できるのかを調べてみましょう！

まず、理解のため(14.1)を最初の3項だけ展開します。

\begin{align*}
f_F (x)=\frac{1}{2}+\frac{2}{\pi }\sin x+\frac{2}{3\pi }\sin 3x\tag{15}
\end{align*}

※\(n=3\)まで展開しました。

これを\(n=0\)、\(n=1\)、\(n=2\)、\(n=3\)を別々でグラフに書くと以下のようになります。

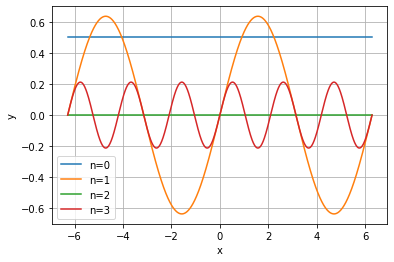
これらの別手の項を順に足していくと、元の関数\(f(x)\)に近づくのかをプログラムを書いて試してみましょう。

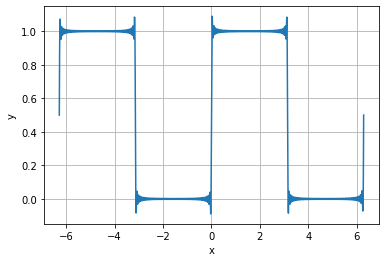
これらを\(n=100\)まで足し合わせていくと、どうなるのかというと、

\begin{align*}
f_F (x)=\frac{1}{2}+\sum_{n=1}^{100}\frac{1-(-1)^n}{\pi n}\sin nx\tag{16}
\end{align*}

こうなります。
【コードも書いておきます】

Google Colabで試してみてください！
\(n\)の数をどんどん増やしていくと、\(f(x)\)にどんどん近づくのですが、不連続点ではいっこうにギザギザが消えないのが確認できると思います。

めちゃくちゃ↓これに近づきましたね！！しかし、繰り返しになりますが、ギブスの現象と呼ばれるギザギザは和をどれだけ増やしても消えることはありません。

以上ポイントをまとめておくと、

不連続な周期関数をフーリエ級数展開すると、不連続点でどれだけ和と足しても消えないギブスの現象と呼ばれるギザギザが残ります。

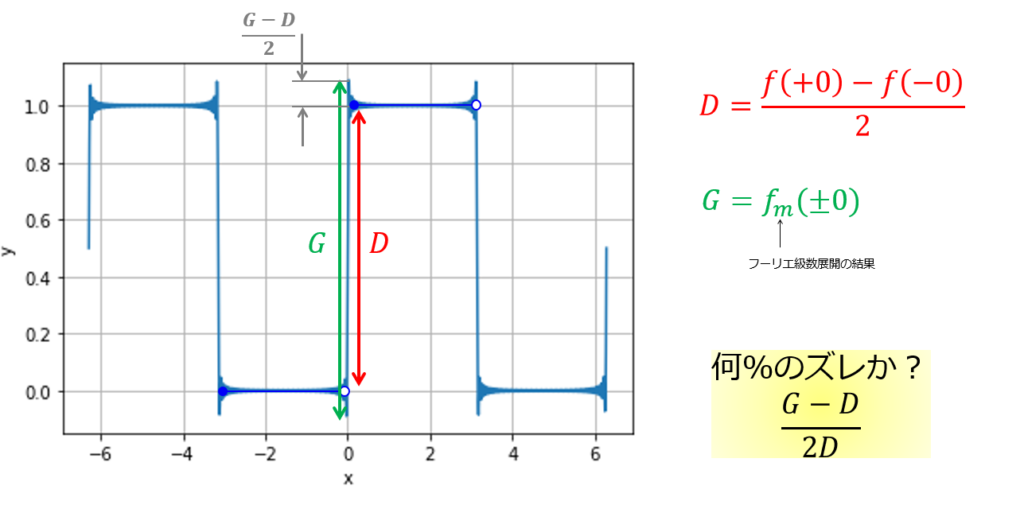
では、不連続点で元の関数とフーリエ級数展開での関数は何%の差があるのかを見てみましょう。

不連続点での差（何％のズレがあるのか？）

ここでは、数学的な証明はせずに先ほど数値計算した結果をそのまま使いましょう。

■まず、元の関数\(f(x)\)の\(x=0\)での値というのは、収束定理より不連続点での平均で書くことができます。

\begin{align*}
D=\frac{f(+0)-f(-0)}{2}=0\tag{17}
\end{align*}

※そういうものだと信じましょう。ただ平均をとっただけだし。

■次に、フーリエ級数展開した関数\(f_{m}(x)\)での\(x=0\)での値を求めます。

理論計算で示すことできるのですが、さきほど書いたプログラムを使って値だけ拾ってみましょう。

最大値を表示すればよいので、「1.0895・・・」と出てきました

 

以上をまとめると以下のようになります。

\begin{align*}
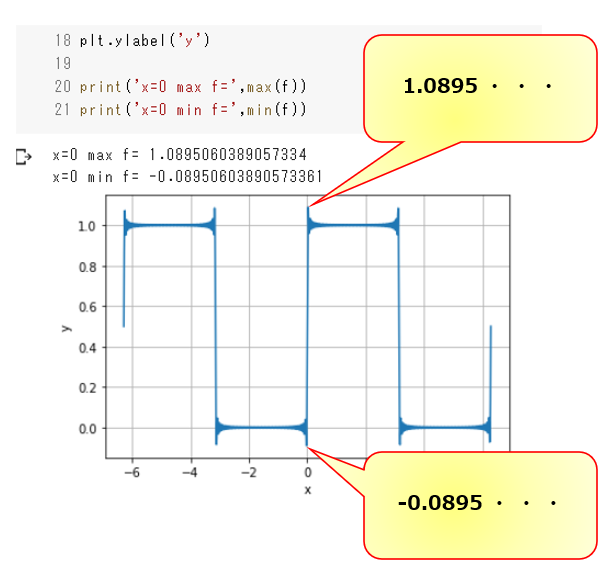
\frac{G-D}{2D}&=\frac{(1.0895-(-1.0895))-1}{2\times 1}=0.0895\tag{18}
\end{align*}

ということで約9%(8.95%)ほどのズレという事がわかりました。

まとめ

今回は、演習問題として下記の関数をフーリエ級数展開してみました。

このようにフーリエ級数展開できます。
\begin{align*}
f_F (x)=\frac{1}{2}+\sum_{n=1}^{\infty}\frac{1-(-1)^n}{\pi n}\sin nx\tag{14.1}
\end{align*}

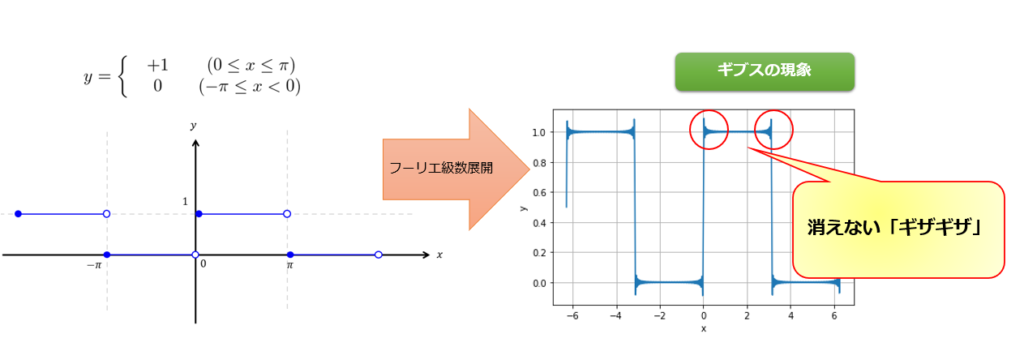
しかし、不連続点では、フーリエ級数展開によるギブスの現象と呼ばれるギザギザがでてしまうことについて見てみました。

大事なところをまとめておくと、とりあえず関数\(f(x)\)の不連続点でギブスの現象と呼ばれるギザギザが出るよということです。

さらに、不連続点で元の関数とフーリエ級数展開での関数は約9%の差ということがわかりました。

数学的な計算は下記の演習書に記載がありました。

勉強はインプットだけではなく、アウトプットが大事ですね。
こちらの演習書は、演習+解説だけではなく補足の説明もしっかり書かれているので、フーリエ解析であまり書かれていない内容も結構乗っています。

フーリエ解析がとても苦手だなという方は、マセマの参考書がお勧めですね。

高校生で数学・物理を教える予備校の先生方が書いた参考書なので高校生でも理解できるように順序立てて説明してくれるため、挫折はしないでしょう。

関連記事もどうぞ

COMMENT