物理数学

解析学

微分積分

  1. 必ずわかる！微分・全微分・偏微分
  2. 全微分と偏微分の違いを視覚的に理解しておく
  3. テーラー展開とその利用方法
  4. 楕円の面積と楕円体の体積の求め方
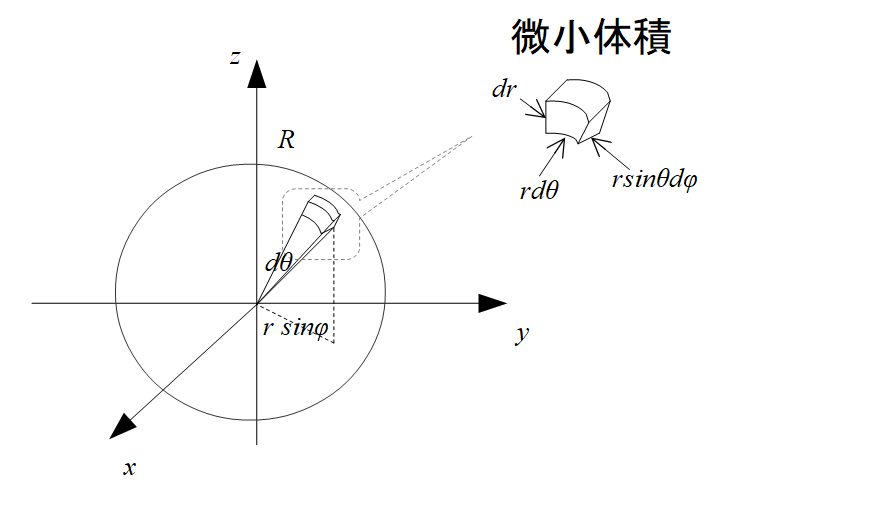
  5. n次元空間における半径Rの球の体積
  6. 2次元・3次元・4次元・5次元(高次元)の球の体積

線形代数

  1. 【線形代数】線形独立と線形関係式
  2. 【はじめて学ぶ線形代数(0回)】新大学生向けに線形代数を書く
  3. 【はじめて学ぶ線形代数(1回)】ベクトルの和と実数倍
  4. 【内積とは（スカラー積とは）】具体的な計算方法と力学の仕事を理解する。
  5. 【外積とは（ベクトル積とは）】具体的な計算方法と力学のモーメントを理解する。
  6. 【行列の掛け算】高校生からわかる線形代数入門。
  7. 【転置行列の性質】積の転置行列の証明あり。
  8. 【なぜ行列式の計算するのか？】逆行列を持つ条件とは。
  9. 【行列式の計算（サラスの公式）】3次正方行列は簡単。
  10. 【置換：行列式の定義】3次の正方行列式を求めてみよう。
  11. 【置換：行列式の定義】4次の正方行列式を求めてみよう。
  12. 【余因子・余因子展開】3次・4次の正方行列式を求めてみよう。
  13. 【行列式の重要な性質】定数倍したものを別の行か列に足しても行列式は変化しない。
  14. 【逆行列とは何か？】逆行列の定義を丁寧に解説する
  15. 【逆行列の計算演習】3行3列の逆行列を余因子行列から求めてみよう
  16. 【例題演習】クラメルの公式を使って連立方程式を解く
  17. 【掃きだし法】拡大係数行列を使って連立１次方程式を解く
  18. 線形独立と線形従属をわかりやすく解説
  19. 【固有値方程式】固有値と固有ベクトルとは何か？
  20. 【行列の対角化】固有値方程式の固有値と固有ベクトルから対角行列をつくる
  21. 【基底変換】基底の変換行列をわかりやすく解説
  22. 【基底変換】固有ベクトルを基底に持つ変換行列は対角行列になる
  23. シュミットの直交化法
  24. ジョルダン標準形

ベクトル解析

  1. ナブラ演算子の基礎を理解する3つのメリット。
  2. 初学者のためのナブラ演算子を用いた「勾配grad」「発散div」「回転rot」

統計学

  1. 【偏差値とは何か】具体的な計算方法をわかりやすく解説！偏差値70以上は優秀
  2. 【母集団と標本集団の違い】高校生からわかる統計学の入門

フーリエ変換

高校生でも理解できる数学

  1. 指数関数の逆関数は対数関数であることをPythonを使いながら解説
  2. 指数関数の意味。高校生からわかる近似曲線に指数関数を選ぶとき
  3. 高校生からわかる片対数グラフと両対数グラフを使うと直線になる理由
  4. 【コロナ感染者数が指数関数増加？】指数関数の特徴3つ覚えておこう。